рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации
Реферат Курсовая Конспект
Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации
Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации - раздел Философия, Лекция 9. Синтез КИХ-фильтров методом наилучшей равномерной чебышевской аппроксимации Постановка Задачи: Синтезировать Оптимальный Ких-Фильтр С Лфчх. О...
Постановка задачи: синтезировать оптимальный КИХ-фильтр с ЛФЧХ.
Оптимальный КИХ-фильтр — это КИХ-фильтр минимального порядка при заданных требованиях к АЧХ.
Метод наилучшей равномерной (чебышевской) аппроксимации включает в себя следующие этапы:
1. Задание аппроксимируемой функции.
При синтезе КИХ-фильтра – это идеальная АЧХ.
Проиллюстрируем на примере ФНЧ.
Аппроксимируемая АЧХ (рис. 9.1) — непрерывная функция на интервале аппроксимации 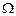 , включающему ПП и ПЗ.
, включающему ПП и ПЗ.
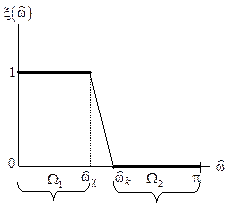
Рис. 9.1. АЧХ идеального КИХ-фильтра ФНЧ
2. Выбор класса аппроксимирующих функций.
В качестве КИХ-фильтра выберем КИХ-фильтра 1-го типа.
Для него класс аппроксимирующих функций — это тригонометрический полином, описывающий амплитудную функцию (см. табл. в Лекции 7):
 , (9.1)
, (9.1)
где  — порядок полинома (для КИХ-фильтра 1-го типа):
— порядок полинома (для КИХ-фильтра 1-го типа):
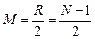 , (9.2)
, (9.2)
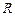 —
—
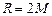 , (9.3)
, (9.3)
 – длина КИХ-фильтра, на основании (9.2) равная:
– длина КИХ-фильтра, на основании (9.2) равная:
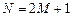 ; (9.3)
; (9.3)
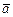 ¾ вектор неизвестных коэффициентов
¾ вектор неизвестных коэффициентов 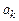 .
.
АЧХ 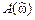 КИХ-фильтра:
КИХ-фильтра:
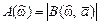 . (9.4)
. (9.4)
Для КИХ-фильтра синтез сводится к расчету
ИХ 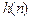 связана с коэффициентами
связана с коэффициентами 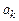 (см. табл. в Лекции 7):
(см. табл. в Лекции 7):
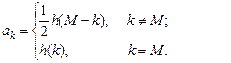 (9.5)
(9.5)
Следовательно, в методе чебышевской аппроксимации синтез КИХ-фильтра сводится к расчету
3. Выбор полинома 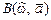 наилучшего приближения к аппроксимируемой функции
наилучшего приближения к аппроксимируемой функции 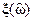 .
.
Полином наилучшего приближения 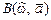 выбирается по критерию Чебышева:
выбирается по критерию Чебышева:
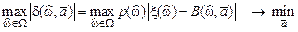 , (9.6)
, (9.6)
где 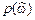 — весовая функция, а
— весовая функция, а 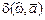 — взвешенная ошибка аппроксимации.
— взвешенная ошибка аппроксимации.
Согласно критерию Чебышева полиномом наилучшего приближения будет тот, который
Поэтому критерий Чебышева называют также
Весовая функция 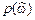 управляет значением модуля максимума ошибки аппроксимации на интервале аппроксимации
управляет значением модуля максимума ошибки аппроксимации на интервале аппроксимации 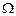 (в ПП и ПЗ).
(в ПП и ПЗ).
Вес, равный 1, присваивается полосе с наибольшим отклонением. Веса в остальных полосах определяются как отношение максимального отклонения к максимальному отклонению в данной полосе.
– Конец работы –
Эта тема принадлежит разделу:
Лекция 9. Синтез КИХ-фильтров методом наилучшей равномерной чебышевской аппроксимации
Синтез КИХ фильтров методом наилучшей равномерной чебышевской аппроксимации... Теорема Чебышева и следствия из нее... Итерационная процедура синтеза оптимального КИХ фильтра Синтез КИХ фильтров методом наилучшей...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Синтез КИХ-фильтров методом наилучшей равномерной (чебышевской) аппроксимации
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов