рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- IV. Обработка результатов научных исследований
Реферат Курсовая Конспект
IV. Обработка результатов научных исследований
IV. Обработка результатов научных исследований - раздел Философия, Проблематика систем ТГСиВ Во Многих Случаях Необходимо Исследовать Случайные, Вероятные...
Во многих случаях необходимо исследовать случайные, вероятные процессы. Обычно технологические процессы выполняются в условиях непрерывного меняющейся обстановки: вынужденные простои машин, неравномерная работа транспорта, непрерывное изменение внешних факторов и т.д. Те или иные события могут произойти или не произойти. В связи с этим приходится анализировать случайные, вероятностные связи, в которых каждому аргументу соответствует множество значений функции. Наблюдения показали, что, несмотря на случайный характер связи, рассеивание имеет вполне определенные закономерности. Для таких статистических законов теория вероятностей позволяет представить исход не одного какого-либо события, а средний результат случайных событий и тем точнее, чем больше число анализируемых явлений. Это связано с тем, что, несмотря на случайный характер событий, они подчиняются определенным закономерностям, рассматриваемым в теории вероятностей.
Теория вероятностей изучает случайные события и базируется на следующих основных показателях. Совокупность множества однородных событий случайной величины х составляет первичный статистический материал. Совокупность, содержащая самые различные варианты массового явления, называют генеральной совокупностью или большой выборкой N. Обычно изучают лишь часть генеральной совокупности, называемой выборочной совокупностью или малой выборкой N1. Вероятностью р(х) события х называют отношение числа случаев N(х), которые приводят к наступлению события х к общему числу возможных случаев N:

Теория вероятностей рассматривает теоретические распределения случайных величин и их характеристики.
Математическая статистика занимается способами обработки и анализа эмпирических событий. Эти две науки составляют единую математическую теорию массовых случайных процессов, широко применяемую в научных исследованиях.
В математической статистике большое значение имеет понятие о частоте событий , представляющего собой отношение числа случаев n(x), при которых имело место событие к общему числу событий n:
, представляющего собой отношение числа случаев n(x), при которых имело место событие к общему числу событий n:

При неограниченном возрастании числа событий частота y(x) стремится к вероятности р(х). Частота 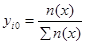 характеризует вероятность появлений случайной величины и представляет собой ряд распределения (рис.1), а плавная кривая – закон распределения F(x).
характеризует вероятность появлений случайной величины и представляет собой ряд распределения (рис.1), а плавная кривая – закон распределения F(x).
Вероятность случайной величины (события) – это количественная оценка возможности ее появления. Достоверное событие имеет вероятность р=1, невозможное событие р=0. Следовательно, для случайного события
0≤ р(х) ≤ 1, а сумма вероятностей всех возможных значений:
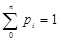
В исследованиях иногда недостаточно знать функцию распределения. Необходимо еще иметь ее характеристики: среднеарифметическое и математическое ожидания, дисперсию, размах ряда распределения.
Пусть среди n событий случайная величина х1 повторяется n1 раз, величина х2 – n2 раза и т.д. Тогда среднеарифметическое значение х имеет вид:
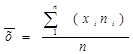
Размах можно использовать для ориентировочной оценки вариации ряда событий:

 где: - максимальное и минимальное значение измерительной величины или погрешности.
где: - максимальное и минимальное значение измерительной величины или погрешности.
Если вместо эмпирических частот y1 ….. yn принять их вероятности
р1 …..рn, то это даст важную характеристику распределения – математическое ожидание:

Для непрерывных случайных величин математическое ожидание определяется интегралом:
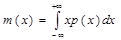
т.е. оно равно действительному значению хд наблюдаемых событий. Таким образом, если систематические погрешности измерений полностью исключены, то истинное значение измеряемой величины равно математическому ожиданию, а соответствующая ему абсцисса называется центром распределения. Площадь, расположенная под кривой распределения (рис.1), соответствующая единице, т.к. кривая охватывает все результаты измерений. Для одной и той же площади можно построить большое количество кривых распределения, т.е. они могут иметь различное рассеяние. Мерой рассеяния (точности измерений) является дисперсия или среднеквадратичное отклонение. Таким образом, дисперсия характеризует рассеивание случайной величины по отношению к математическому ожиданию и вычисляется по формуле:

Важной характеристикой теоретической кривой распределения является среднеквадратичное отклонение:

Коэффициент вариации
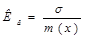
применяется для сравнения интенсивности рассеяния в различных совокупностях, определяется в относительных единицах (kв <1).
Основной задачей статистики является подбор теоретических кривых по имеющемуся эмпирическому закону распределения. Пусть в результате n измерений случайной величины получен ряд ее значений х1, х2, х3, …., хn. При первичной обработке таких рядов их вначале группируют в интервалы и устанавливают для каждого из них частоты 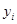 и
и 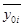 . По значениям хi и
. По значениям хi и 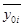 строят ступенчатую гистограмму частот и вычисляют характеристики эмпирической кривой распределения. Основными характеристиками эмпирического распределения являются:
строят ступенчатую гистограмму частот и вычисляют характеристики эмпирической кривой распределения. Основными характеристиками эмпирического распределения являются:
среднеарифметическое значение:
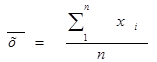

дисперсия:
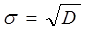
Значения этих величин соответствуют величинам 
 и
и 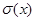 теоретического распределения.
теоретического распределения.
Уравнение 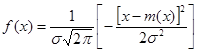 соответствует функции нормального распределения при m(x)
соответствует функции нормального распределения при m(x)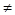 0 (рис. 2, а). Если совместить ось ординат с точкой m, т.е. m(x)=0 (рис.2,б), и принять
0 (рис. 2, а). Если совместить ось ординат с точкой m, т.е. m(x)=0 (рис.2,б), и принять 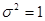 , то знаки нормального распределения описываются зависимостью:
, то знаки нормального распределения описываются зависимостью:
Для оценки рассеяния обычно пользуются величиной  . Чем меньше
. Чем меньше  , тем меньше рассеяние, т.е. большинство наблюдений мало отличается друг от друга (рис.3). С увеличением
, тем меньше рассеяние, т.е. большинство наблюдений мало отличается друг от друга (рис.3). С увеличением  рассеяние возрастает, вероятность появления больших погрешностей увеличивается, а максимум кривой распределения (ордината), равная
рассеяние возрастает, вероятность появления больших погрешностей увеличивается, а максимум кривой распределения (ордината), равная  уменьшается. Поэтому величину
уменьшается. Поэтому величину 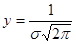 при
при 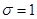 или
или 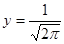 называют мерой точности.
называют мерой точности.
Таким образом, чем меньше  , тем больше сходимость результатов измерений, а ряд измерений более точен, среднеквадратичное отклонение определяет закон распределения. Отклонения +
, тем больше сходимость результатов измерений, а ряд измерений более точен, среднеквадратичное отклонение определяет закон распределения. Отклонения + и -
и - соответствуют точкам перегиба кривой (заштрихованная площадь на рис. 3). В общем случае для предела
соответствуют точкам перегиба кривой (заштрихованная площадь на рис. 3). В общем случае для предела 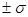 вероятность того, что событие хiпопадает в данный предел, вычисляется по распределению Лапласа:
вероятность того, что событие хiпопадает в данный предел, вычисляется по распределению Лапласа:

При анализе многих случайных дискретных процессов пользуются распределением Пуассона. Так, вероятность появления числа событий х=1,2,3,… в единицу времени определяется законом Пуассона (рис.4) и подсчитывается по формуле:
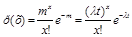
Гдех – число событийза данный отрезок времени t;
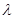 - плотность, т.е. среднее число событий за единицу времени;
- плотность, т.е. среднее число событий за единицу времени;
 - число событий за время t,
- число событий за время t,  = m
= m
Распределение Пуассона относят к редким событиям, т.е. р(х) – вероятность того, что событие в период какого-то испытания произойдет х раз при очень большом числе измерений m. Для закона Пуассона дисперсия равна математическому ожиданию числа наступления события за время t, т.е. 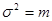
Для исследования количественных характеристик некоторых процессов можно применять показательный закон распределения (рис. 5). Плотность вероятности показательного закона выражается зависимостью  . Здесь плотность является величиной, обратной математическому ожиданию
. Здесь плотность является величиной, обратной математическому ожиданию 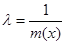 , кроме того
, кроме того 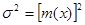 .
.
В различных областях исследований широко применяется закон распределения Вейбулла (рис.6). 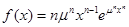 , где n,
, где n, - параметры закона; х – аргумент (чаще принимаемый как время).
- параметры закона; х – аргумент (чаще принимаемый как время).
Исследуя процессы, связанные с постепенным снижением параметров (ухудшением свойств материалов во времени, деградация конструкций, процессы старения, износовые отказы в машинах и др.), применяют закон  - распределения (рис. 7).
- распределения (рис. 7). 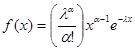 ; где
; где  - параметры. Если
- параметры. Если 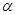 = 1,
= 1,  - функция превращается в показательный закон.
- функция превращается в показательный закон.
При исследовании многих процессов, связанных с установлением расчетных характеристик, материалов и т.п., используют закон распределения Пирсона (рис.8), чаще всего представляемый в виде:

где а – максимальная ордината; d,b – соответственно расстояния от максимальной ординаты до центра распределения С и начала координат 0.
Кроме приведенных выше применяют и другие виды распределений. В исследованиях часто возникает необходимость выявления факторов или их комбинаций, существенно влияющих на исследуемый процесс, так как при измерении какой-либо величины результаты обычно зависят от многих факторов. Практика показывает, что основными факторами, как правило, являются техническое состояние прибора и внимание оператора. Для установления основных факторов и их влияния на исследуемый процесс используется дисперсионный одно- и многофакторный анализ. Суть однофакторного дисперсионного анализа рассмотрим на примере. Пусть необходимо проверить степень точности группы m приборов и установить, являются ли их систематические ошибки одинаковыми, т.е. изучить влияние одного фактора – прибора на погрешность измерения. Каждым прибором выполнено n измерений одного и того же объекта, а всего nm измерений. Отдельное измерение хij, где i – номер прибора, имеющий значение от 1 до m; j- номер выполненного на этом приборе измерения, изменяющийся от 1 до n.Дисперсионный анализ допускает, что отклонения подчиняются нормальному закону распределения, в соответствии с которым вычисляют для каждой серии измерений среднеарифметическое значение и среднюю из показаний первого прибора и т.д. для каждого из niизмерений иmiприборов.В результате расчетов устанавливают величину Q1, называемую суммой квадратов отклонений между измерениями серий:

Она показывает степень расхождения в систематических погрешностях всехmприборов, т.е. характеризует рассеивание исследуемого фактора между приборами.
Здесь -среднеарифметическое для n измерений;
-среднеарифметическое для n измерений;
 - среднеарифметическое для всех серий измерений, т.е. общее среднее значение.
- среднеарифметическое для всех серий измерений, т.е. общее среднее значение.
Определяется также величина Q2

где хij- отдельноеi-еизмерение наj-омприборе.
Величину Q2 называют суммой квадратов отклонений внутри серии. Она характеризует остаточное рассеивание случайных погрешностей одного прибора.
При таком анализе допускается, что центры нормальных распределений случайных величин равны, в связи с чем все mn измерения можно рассматривать как выборку из одной и той же нормальной совокупности. Чтобы убедиться в возможности такого допущения, вычисляют критерий:
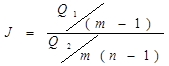
Числитель и знаменатель представляют собой дисперсию  для m и mnнаблюдений. В зависимости от значений k1 = m-1 и k2 = m(n-1) числа степеней свободы и вероятности р составлены табличные значения Jт. Если J ≤ Jт то считается, что в данном примере все приборы имеют одинаковые систематические ошибки.
для m и mnнаблюдений. В зависимости от значений k1 = m-1 и k2 = m(n-1) числа степеней свободы и вероятности р составлены табличные значения Jт. Если J ≤ Jт то считается, что в данном примере все приборы имеют одинаковые систематические ошибки.
Дисперсионный анализ является многофакторным, если он имеет два фактора и более. Суть его принципиально не отличается от однофакторного, но существенно увеличивается количество расчетов.
Методы теории вероятностей и математической статистики часто применяют в теории надежности, широко используемой в различных отраслях науки и техники. Под надежностью понимают свойство изделия (объекта) выполнять заданные функции (сохранять установленные эксплутационные показатели) в течение требуемого периода времени. В теории надежности отказы рассматривают как случайные события. Для количественного описания отказов применяются математические модели – функции распределения вероятностей интервалов времени.
Основной задачей теории надежности является прогнозирование (предсказание с той или иной вероятностью) различных показателей безотказной работы (долговечности, срока службы и т.д.), что связано с нахождением вероятностей.
Для исследования сложных процессов вероятностного характера применяют метод Монте-Карло, с помощью которого отыскивается наилучшее решение из множества рассматриваемых вариантов. Результаты решения метода позволяют установить эмпирические зависимость исследуемых процессов. Математической основой метода является закон больших чисел: при большом числе статистических испытаний вероятность того, что среднеарифметическое значение случайной величины стремится к ее математическому ожиданию, равна 1, т.е.
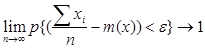
где  - любое малое положительное число.
- любое малое положительное число.
Из этой формулы видно, что по мере увеличения числа испытаний n среднеарифметическое неограниченно (асимптотически) приближается к математическому ожиданию.
Для решения задач методом Монте-Карло необходимо иметь статистический ряд, знать закон его распределения, среднее значение  , математическое ожидание
, математическое ожидание 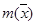 и среднеквадратичное отклонение. С помощью метода можно получить сколько угодно заданную точность решения.
и среднеквадратичное отклонение. С помощью метода можно получить сколько угодно заданную точность решения.
– Конец работы –
Эта тема принадлежит разделу:
Проблематика систем ТГСиВ
Трудно назвать отрасль народного хозяйства в которой не применялась бы... Теплогазоснабжение и вентиляция как самостоятельная отрасль науки и техники сформировалась относительно недавно...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: IV. Обработка результатов научных исследований
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов