рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Формула Гаусса-Остроградського.
Реферат Курсовая Конспект
Формула Гаусса-Остроградського.
Формула Гаусса-Остроградського. - раздел Философия, 15. Формула Гріна. 17. Поверхневий інтеграл I роду; Обчислити його. 18.Криволінійний інтеграл 2 роду; обчислення. 19.Теорема про рівність нулеві криволінійного інтеграла 2 роду по простому замкненому контуру. Формула Гаусса-Остроградського Встановлює Зв'язок Поверхневого Інтегралу Іі Р...
Формула Гаусса-Остроградського встановлює зв'язок поверхневого інтегралу ІІ роду по замкненій поверхні з потрійним інтегралом по просторовій області, яка обмежена цією поверхнею.
Теорема.
Нехай 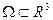 – обмежена область, межа якої
– обмежена область, межа якої 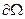 – кусково-гладка поверхня, орієнтована зовнішніми нормалями. В області
– кусково-гладка поверхня, орієнтована зовнішніми нормалями. В області 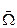 задано неперервно диференційовне поле
задано неперервно диференційовне поле 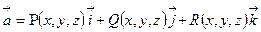 . Тоді потік векторного поля
. Тоді потік векторного поля 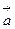 через межу області
через межу області 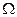 дорівнює потрійному інтегралу від
дорівнює потрійному інтегралу від 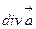 по області
по області 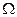 , тобто
, тобто 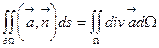 (1) або
(1) або 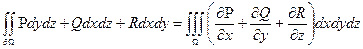 (2). Формулу (1) або (2) називають формулою Гаусса-Остроградського; відповідно у векторній формі (1) і координатній (2).
(2). Формулу (1) або (2) називають формулою Гаусса-Остроградського; відповідно у векторній формі (1) і координатній (2).
○ Розглянемо область  , яка є правильною (елементарною) відносно осі
, яка є правильною (елементарною) відносно осі  і обмежена поверхнями
і обмежена поверхнями 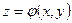 ,
,  . Область
. Область 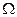 проектується на площину
проектується на площину 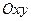 в правильну область
в правильну область  , в якій функції
, в якій функції 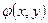 ,
,  є неперервними. Поверхня
є неперервними. Поверхня 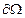 є об’єднанням поверхонь
є об’єднанням поверхонь 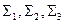 . При заданих умовах існує потрійний інтеграл
. При заданих умовах існує потрійний інтеграл  і його можна записати у вигляді повторного інтеграла:
і його можна записати у вигляді повторного інтеграла:  (3)
(3)
В цій формулі дописали третій доданок, оскільки 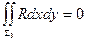 . Рівність (3) можна записати так:
. Рівність (3) можна записати так: 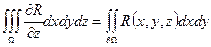 (4). Можна показати, що формула (4) є правильною для області, обмеженої довільними кусково-гладкими поверхнями (розбиваючи їх на елементарні частини). Аналогічно можна отримати рівності
(4). Можна показати, що формула (4) є правильною для області, обмеженої довільними кусково-гладкими поверхнями (розбиваючи їх на елементарні частини). Аналогічно можна отримати рівності  (5), де область
(5), де область 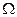 – правильна відносно осі
– правильна відносно осі 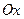 ;
; 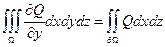 (6), де
(6), де 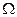 – правильна область відносно осі
– правильна область відносно осі 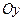 . Тепер, нехай область
. Тепер, нехай область 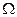 є правильною відносно трьох осей одночасно. Тоді, додавши відповідно праві і ліві частини рівностей (4), (5), (6) отримаємо формулу Гаусса-Остроградського (2). ●
є правильною відносно трьох осей одночасно. Тоді, додавши відповідно праві і ліві частини рівностей (4), (5), (6) отримаємо формулу Гаусса-Остроградського (2). ●
Зауваження. Якщо покласти 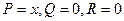 , то за формулою (2) можна обчислити об’єм області
, то за формулою (2) можна обчислити об’єм області 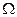 :
: 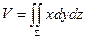 , де
, де 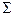 – поверхня, що обмежує область
– поверхня, що обмежує область 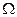 . Якщо
. Якщо 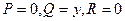 , то
, то 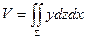 . Якщо
. Якщо 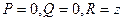 , то
, то  . Якщо
. Якщо 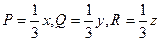 , то об’єм області
, то об’єм області 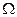 , обмежений поверхнею
, обмежений поверхнею 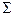 можна обчислити за формулою:
можна обчислити за формулою:  .
.
– Конец работы –
Эта тема принадлежит разделу:
15. Формула Гріна. 17. Поверхневий інтеграл I роду; Обчислити його. 18.Криволінійний інтеграл 2 роду; обчислення. 19.Теорема про рівність нулеві криволінійного інтеграла 2 роду по простому замкненому контуру.
Формула Гріна... Формула Гріна встановлює зв язок між подвійним інтегралом і криволінійним інтегралом роду...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Формула Гаусса-Остроградського.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов