П.2 Предел функции.

Определение1. Число а называется пределом функции у=f(х), при х стремящемся к х₀ (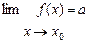), если для любой последовательности{x_n} сходящейся к x₀ последовательность{f(x_n)=y_n} сходится к а.

Из определения 1 следует, что для предела функции справедливы все теоремы, справедливые для предела последовательности.

Определение2. Число а называется пределом функции у=f(x) при х стремящимся к х₀ (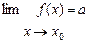),если "e>0 $ d>0 "х ½х-х₀½<dÞ½f(x)-a½<e. Легко показать, что определение1 равносильно определению2. Мы будем пользоваться обоими этими определениями.

Теорема1. (1-ый замечательный предел)

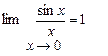
Доказательство.1)Пусть х>0, т.е. х-угол, измеренный в радианах, лежащий в 1-ой четверти. Дан тригонометрический круг (окружность радиуса R=1). Рассмотрим треугольник ОАВ, сектор ОАВ и треугольник ОСВ.

S_OAB< S_{сектора}< S_OCB

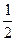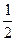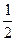ОВ ·АН<хR<ОВ·СВ

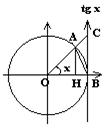OB·AH<xR<OB·CB

OB=R=1, AH=sinx, CB=tgx.

Таким образом 0<sinx<x<tgx. Поделим все части этого неравенства на sinx>0.

0<1<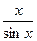<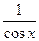. Перевернём все дроби

0<cosx<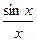<1. (1)

При х®0, cosx®1, 1®1.

По лемме о 2-х милиционерах 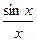®1при х®0.

2) Пусть -х<0, т.е. –х-угол в IV четверти. В неравенстве (1) везде вместо х подставим -х

cos(-x)=cosx, ==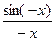

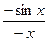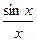
Ни одна величина в (1) не изменилась, значит неравенство справедливо при -хÎIV четверти. Теорема1 доказана.

Теорема2. (2-ой замечательный предел)

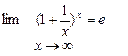(или в равносильной формулировке ).

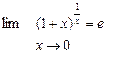Теорема3. (Бином Ньютона)

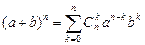, где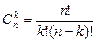

или в более подробной записи

(а+b)ⁿ=aⁿ+na^n-1b+C_n²a^n-2b²+C_n³a^n-3b³+¼+C_n^n-2a²b^n-2+na^n-1b+bⁿ.