Сравнительная оценка экономической эффективности территориальных информационных систем.

При использовании той или иной методики расчета сравнительной эффективности важно правильно определять совокупность затрат на создание ИС и правильно прогнозировать возможные результаты.

С позиций пользователя информационной системы абсолютная эффективность автоматизации определяется как разность между полученными результатами (или оценкой этих результатов в будущем) и затратами на автоматизацию. Для повышения степени адекватности оценок эффективности необходимо перейти к так называемым приведенным оценкам. В этом случае проект автоматизации рассматривается как растянутый во времени поток платежей, включающий как поступления, так и расход денежных средств. Сумму платежей потока определяют методом дисконтирования, получая так называемую приведенную стоимость потока платежей, которая и является критерием сравнения.

Рассмотрим теорию дисконтирования. Основной принцип финансовых расчетов состоит в неравноценности денежных сумм, принадлежащих разным моментам времени. И это естественно: деньги, полученные «сейчас», можно, например, положить на банковский счет, и к некоторому времени к ним добавится прибыль — проценты. Можно использовать какой-либо другой способ наращения денег. Автоматизация предприятия — это проект, требующий денежных затрат и, предположительно, приносящий определенную прибыль. Оценку эффективности осуществляют, сравнивая прибыльность проекта с прибыльностью банковского депозита. Данный подход весьма распространен.

Наращенная сумма есть результат сложения суммы, предоставляемой в кредит, и процентных денег.

Формула определения наращенной суммы с использованием простых процентов (формула простых процентов) запишется в следующем виде:

S = P+P*n*i = P*(1+n*i),

где S — наращенная сумма;

Р — начальная сумма;

n — срок наращения;

i — процентная ставка.

Выражение (1+ n*Г) называется множителем наращения простых процентов.

Термин «дисконтирование» употребляется в финансовом управлении весьма широко. Под этим термином может пониматься способ нахождения величины Р на некоторый момент времени при условии, что в будущем при начислении на нее процентов она могла бы составить наращенную сумму S. Величину Р, найденную дисконтированием наращенной величины S, называют современной или приведенной величиной. С помощью дисконтирования в финансовых вычислениях учитывается фактор времени.

Существуют математический и банковский (коммерческий) методы дисконтирования.

При математическом дисконтировании решается задача, обратная определению наращенной суммы. Сформулируем ее следующим образом: какую сумму следует выдать в долг на n лет, чтобы при начислении на нее процентов по ставке i получить наращенную сумму, равную S?

Для решения этой задачи используем формулу наращения по простой ставке процентов, тогда:

P=S/(1+ п*i)

В финансовой практике широко используются сложные проценты. Основное отличие сложных процентов от простых заключается в том, что база для начисления процентов меняется от одного расчетного пе­риода к другому. Сумма начисленных в каждом периоде процентов добавляется к капиталу предыдущего периода, а начисление процен­тов в последующем периоде производится на эту, уже наращенную величину первоначального капитала. Процесс наращения капитала в этом случае описывается геометрической прогрессией. Способ вычис­ления процентов платежей по сложным процентам иногда называется вычислением «процента на процент». Механизм наращения первона­чальной суммы (капитала) по сложным процентам называют капита­лизацией.

Различают годовую капитализацию (процентный платеж начисля­ется и присоединяется к ранее наращенной сумме в конце года), полу­годовую, квартальную, месячную и ежедневную.

Величину первоначальной суммы (капитала), на которую начисля­ются проценты, т. е. текущую стоимость капитала, обозначим через Р. Сумму, полученную в результате начисления сложных процентов на текущую стоимость, будем называть наращенной суммой или конеч­ной стоимостью капитала S.

Процентную ставку и срок ссуды обозначим соответственно через i и n.

Сумма S, наращенная за n лет при начислении сложных процентов по ставке i, рассчитывается по формуле:

S = P*(l + i)ⁿ.

Величину (1+i)ⁿ называют множителем наращения сложных процентов.

Математический метод дисконтирования может применяться с использованием не только простой, но и сложной процентной ставки:

где (1 + i)^-n — дисконтный (учетный) множитель.

Современная величина, являясь одной из основных характеристик, используемых в финансовом анализе, требует рассмотрения ее основных свойств. Одно из этих свойств заключается в том, что величина процентной ставки, по которой производится дисконтирование, и современная величина находятся в обратной зависимости. То есть чем выше процентная ставка, тем меньше современная величина при прочих равных условиях.

Оплата по заключенным сделкам может предусматривать как разовый платеж, так и ряд выплат, распределенных во времени.

Финансовая рента (далее рента) может быть охарактеризована рядом параметров:

♦ член ренты — величина каждого отдельного платежа;

♦ период ренты — временной интервал между двумя платежами;

♦ срок ренты — время от начала реализации ренты до момента начисления последнего платежа;

♦ процентная ставка — ставка, используемая для расчета наращения или дисконтирования платежей, составляющих ренту.

Кроме перечисленных параметров, рента характеризуется: количеством платежей в течение года, частотой начисления процентов (т.е. количеством периодов в году, когда начисляются проценты), моментом производства платежей (в начале, середине или в конце года) и др.

На практике используются различные виды финансовых рент. Ренты, по которым платежи производятся раз в год, называются годовыми.

Обобщающими показателями ренты являются: наращенная сумма и современная (приведенная) величина.

Наращенная сумма — сумма всех членов потока платежей с начисленными на них процентами на конец срока, т. е. на дату последней выплаты.

Современная величина потока платежей — сумма всех его членов, уменьшенная (дисконтированная) на величину процентной ставки на определенный момент времени, совпадающий с началом потока платежей или предшествующий ему. Современная величина показывает, какую сумму следовало бы иметь первоначально, чтобы, разбив ее на равные взносы, на которые бы начислялись установленные проценты в течение срока ренты, можно было обеспечить получение наращенной суммы. Обобщающие характеристики ренты используются в финансовом анализе при заключении различных коммерческих сделок, для планирования погашения задолженности, сравнения эффективности контрактов, имеющих различные условия их реализации.

Наращенная сумма ренты рассчитывается по формуле:

S=R*((1+i)ⁿ-1)/i

Величина ((1+i)ⁿ-1)/i является коэффициентом наращения ренты.

Предположим:

R — рентный годовой платеж;

i — годовая процентная ставка, начисляемая в конце периода ренты;

n — срок ренты.

Оценка современной величины производится на момент начала реализации ренты.

Современная величина рассчитывается по следующей формуле:

A=R*(1-(1+i)ⁿ)/i

Процентная ставка является показателем доходности финансовых операций.

Для определения процентной ставки i по известным параметрам финансовой ренты существует ряд математических методов. Рассмотрим один из них, имеющий, на наш взгляд, наибольшее практическое значение.

Метод линейной интерполяции. При определении процентной ставки финансовой ренты исходят прежде всего из заданного коэффициента наращения или коэффициента приведения ренты. Иначе — по известным параметрам S или А, а также R и n определяют

s=S/R или a=A/R

Далее вычисление процентной ставки i производится следующим образом:

а) при известных величинах S и R:

где i_(H) и i_(B) верхнее и нижнее значения предполагаемой процентной ставки;

s_(B) и s_(H) — значения коэффициентов наращения при использовании процентных ставок i_(H) и i_(B).

б) при известных величинах A и R:

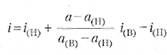
где а_(В) и а_(Н) - значения коэффициента приведения при использовании процентных ставок i_(H) и i_(B).