рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Основные закономерности в антеннах
Реферат Курсовая Конспект
Основные закономерности в антеннах
Основные закономерности в антеннах - раздел Философия, АНТЕННЫ И РАСПРОСТРАНЕНИЕ РАДИОВОЛН Принцип Суперпозиции При Расчете П...
Принцип суперпозиции
При расчете поля антенны в дальней зоне используется принцип суперпозиции (сложения), отражающий свойство электромагнитного поля: поля нескольких источников в данной точке пространства складываются векторно. Применительно к задаче определения поля заданной антенны в дальней зоне использование этого принципа заключается в следующем: вся антенна разбивается на элементарные части, находится поле каждой элементарной части, а затем эти поля суммируются.
В теории антенн по особенностям применения принципа суперпозиции все антенны делятся на три класса - проволочные, щелевые и апертурные.
Апертурная антенна представляет собой некоторую излучающую поверхность (раскрыв или апертуру). Примеры таких антенн: зеркальные, линзовые, волноводные, рупорные антенны. Пусть, например, раскрыв имеет круглую форму и расположен в системе координат X,Y,Z - рис. 2.5. На излучающем раскрыве каким-то образом, например с помощью рупора, (показан пунктиром) создано поле  , где
, где  - амплитуда поля,
- амплитуда поля,  - начальная фаза. Элементарным излучателем такой антенны является бесконечно малый элемент поверхности dS. Так как
- начальная фаза. Элементарным излучателем такой антенны является бесконечно малый элемент поверхности dS. Так как 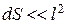 , поле в пределах элемента dS можно считать неизменным по амплитуде и фазе. Такой элементарный излучатель называется источником Гюйгенса. Свойства его изучены в электродинамике. Пусть элемент dS создает в пространстве поле dE. Тогда полное поле всего излучающего раскрыва S будет равно сумме полей всех элементарных излучателей:
, поле в пределах элемента dS можно считать неизменным по амплитуде и фазе. Такой элементарный излучатель называется источником Гюйгенса. Свойства его изучены в электродинамике. Пусть элемент dS создает в пространстве поле dE. Тогда полное поле всего излучающего раскрыва S будет равно сумме полей всех элементарных излучателей:
 .
.
Таким образом, для того чтобы определить поле антенны с помощью принципа суперпозиции, необходимо определить поле элементарных излучателей dE, а затем, зная распределение поля или тока в элементах антенны, определить полное поле путем интегрирования по длине или по излучаемой поверхности антенны.

|
Во всех случаях характеристики и пара-
метры антенны зависят от закона распределе-
ния амплитуд и начальных фаз токов или по
лей, возбуждающих элементарные излучате-
ли, параметров элементарных излучателей,
формы и размеров антенны и частоты. Для
характеристики закона распределения ампли-
туд и фаз возбуждающих токов (полей) по
элементам антенны вводится понятие
Рис. 2.5. Апертурная антенна амплитудно-фазового распределения возбуж-
дения (АФР) возбуждения.
Амплитудное распределение возбуждения (АР) – это распределение амплитуд токов, напряжений или полей, которые возбуждают отдельные элементарные излучатели обозначается символом А(Q). Под Q понимаются координаты точки на антенне, определяющие положение произвольного элементарного излучателя. Координаты могут быть заданы в полярной, сферической или прямоугольной системах. Исходя из применения принципа суперпозиции амплитудное распределение возбуждения для апертурной антенны определяется выражением (рис. 2.5):
 ,
,
где  - распределение амплитуд напряженности электрического поля по апертуре и максимальное значение амплитуды.
- распределение амплитуд напряженности электрического поля по апертуре и максимальное значение амплитуды.
Фазовое распределение возбуждения (ФР) - это зависимость начальной фазы тока, напряжения или поля, возбуждающего элементарный излучатель антенны от координат данного излучателя Q. Обычно фаза в некотором элементарном излучателе отсчитывается от фазы излучателя, принятого за начальный (центральный). Начальным может быть излучатель, расположенный на входе антенны, или в ее центре, или на краю в зависимости от типа антенны. От выбора положения начального излучателя зависит сложность аналитического решения задачи по определению величины поля в дальней зоне антенны, но не зависят характеристики и параметры антенны. Фазовое распределение возбуждения далее обозначается символом (Q) и для апертурной антенны определяется выражением (рис. 2.5)
 ,
,
где  - фазы напряженности поля на излучающем раскрыве антенны в точке Q с координатами x,y и в точке с координатами
- фазы напряженности поля на излучающем раскрыве антенны в точке Q с координатами x,y и в точке с координатами 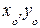 (в центре излучающего раскрыва).
(в центре излучающего раскрыва).
Виды амплитудных распределений возбуждения на излучающих
раскрывах апертурных антенн
Будем для упрощения рассмотрения вопроса считать фазовое распределение возбуждения на излучающем раскрыве апертурной антенны равномерным (синфазный излучающий раскрыв). Рассмотрим виды амплитудных распределений возбуждения на излучающем раскрыве, характерных для апертурных антенн.
В волноводных и рупорных антеннах, выполненных на основе прямоугольного волновода, при возбуждении в них основной волны 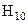 в плоскости «Е» амплитудное распределение возбуждения равномерное
в плоскости «Е» амплитудное распределение возбуждения равномерное 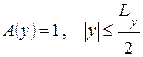 , а в плоскости «Н» - косинусоидальное
, а в плоскости «Н» - косинусоидальное  , где
, где  – линейные размеры открытого конца прямоугольного волновода.
– линейные размеры открытого конца прямоугольного волновода.
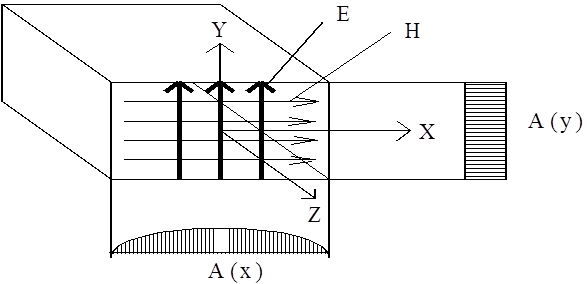
На рис. 2.6 показан излучатель в виде открытого конца прямоугольного волновода в системе координат X, Y, Z, структура силовых линий электрического и магнитного полей на излучающем раскрыве волновода и гистограммой показаны амплитудные распределения возбуждения A(x) - в плоскости «Н» и A(y) - в плоскости «Е». Аналогичные амплитудные распределения возбуждения на излучающем раскрыве Е и Н – плоскостных секториальных рупорных антенн.
|
Рис. 2.6. Структура силовых линий возбуждающего поля и амплитудное распределение возбуждения на открытом конце прямоугольного волновода
В зеркальных, линзовых антеннах амплитудное распределение возбуждения комбинированное - симметрично относительно центра и спадает до некоторого уровня к концам излучающего раскрыва антенны. На рис. 2.7 показана схематически зеркальная антенна, состоящая из параболического металлического отражателя (зеркала) и облучателя. Показаны также диаграмма направленности облучателя в полярных координатах и амплитудное распределение возбуждающего поля A(x) на раскрыве зеркала вдоль оси X. В центре раскрыва A(x)=1, на краях раскрыва относительный уровень поля < 1. Такое амплитудное распределение описывается формулой
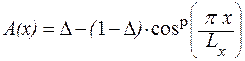 . (2.1) Величина р характеризует скорость спада амплитудного распределения возбуждения от центра излучающего раскрыва антенны к краям, - подставка («пьедестал») в комбинированном амплитудном распределении возбуждения,
. (2.1) Величина р характеризует скорость спада амплитудного распределения возбуждения от центра излучающего раскрыва антенны к краям, - подставка («пьедестал») в комбинированном амплитудном распределении возбуждения,
характеризующая нормированный уровень амплитуды поля на краях раскрыва.
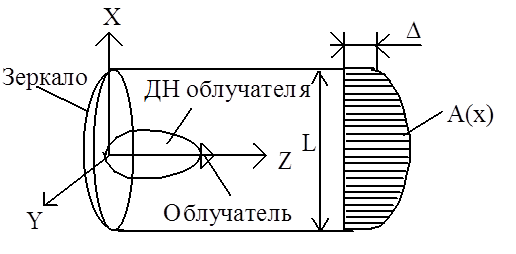
Рис. 2.7. Зеркальная антенна с комбинированным амплитудным
распределением возбуждающего поля на ее излучающем раскрыве
В антенной технике используются и другие амплитудные распределения возбуждения, но все их применительно к линейной антенне можно разделить на симметричные и несимметричные относительно центра антенны.
Виды фазовых распределений возбуждения на излучающих
раскрывах апертурных антенн
Фазовое распределение возбуждения на любой линейной антенне может иметь детерминированную составляющую и случайную. Рассмотрим влияние детерми-нированного фазового распределения возбуждения.
Пусть фазовое распределение описывается некоторой функцией (z). Разложим эту функцию в степенной ряд
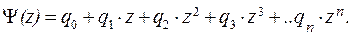 (2.2)
(2.2)
Члены ряда выражения (2.2) представляют собой:
 - равномерное фазовое распределение возбуждения;
- равномерное фазовое распределение возбуждения;
 - линейное фазовое распределение возбуждения;
- линейное фазовое распределение возбуждения;
 - квадратичное фазовое распределение возбуждения;
- квадратичное фазовое распределение возбуждения;
 - кубичное фазовое распределение возбуждения.
- кубичное фазовое распределение возбуждения.
Члены ряда с четными степенями z называются четными фазовыми ошибками, с нечетными степенями z - нечетными фазовыми ошибками. В различных конструкциях антенн эти фазовые ошибки выражены по-разному. Так, например, на излучающем раскрыве антенны в виде открытого конца прямоугольного или круглого волноводов, в зеркальной антенне при расположении облучателя в фокусе параболического зеркала фазовое распределение близко к равномерному.
На раскрыве зеркальной антенны при смещении облучателя вдоль фокальной оси (на рис. 2.7 вдоль оси Z), на раскрыве рупорной антенны фазовое распределение близко к квадратичному. Если облучатель зеркальной антенны незначительно сместить из фокуса зеркала в фокальной плоскости (на рис. 2.7 - перпендикулярно оси Z), на раскрыве появляется линейное фазовое распределение. При большом смещении облучателя в фокальной плоскости на излучающем раскрыве зеркала возрастают фазовые ошибки. В данном случае имеет место кубичное фазовое распределение возбуждения.
Линейное фазовое распределение характеризуется величиной коэффициента замедления  , где
, где 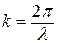 - волновое сопротивление свободного пространства (волновое число).
- волновое сопротивление свободного пространства (волновое число).
Квадратичное и кубическое фазовое распределение характеризуется величиной максимальной фазовой ошибки на краях излучающего раскрыва
апертурной антенны 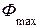 :
:
для квадратичного фазового распределения возбуждения  ,
,
для кубического фазового распределения возбуждения  .
.
Влияние волновых размеров и амплитудно-фазового распределения возбуждения на направленные свойства апертурных антенн
1. С ростом волновых размеров антенны  (
(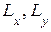 - линейные размеры апертурной антенны, - рабочая длина волны) главный лепесток ее ДН сужается, растет количество боковых лепестков, но их уровень не меняется.
- линейные размеры апертурной антенны, - рабочая длина волны) главный лепесток ее ДН сужается, растет количество боковых лепестков, но их уровень не меняется.
2. При комбинированном амплитудном распределении возбуждения для синфазной апертурной антенны, с ростом уровня подставки и уменьшением скорости спада р от центра раскрыва к его краям, ширина главного лепестка ДН антенны уменьшается, уровень боковых лепестков растет.
3. Ширина главного лепестка ДН по половинной мощности для апертурной антенны в основных плоскостях «Е» и «Н» в общем случае определяется выражениями
 , (2.3)
, (2.3)
где l - рабочая длина волны;
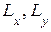 - линейные размеры антенны;
- линейные размеры антенны;
 - коэффициент, зависящий от вида амплитудного распределения
- коэффициент, зависящий от вида амплитудного распределения
возбуждения на излучающем раскрыве антенны.
С ростом уровня подставки в комбинированном амплитудном распределении возбуждения D коэффициент  уменьшается. В данном случае при увеличении скорости спада р амплитудного распределение от центра раскрыва антенны к его краям - коэффициент
уменьшается. В данном случае при увеличении скорости спада р амплитудного распределение от центра раскрыва антенны к его краям - коэффициент  увеличивается.
увеличивается.
4. Задание линейного фазовое распределение возбуждения на раскрыве апертурной антенны приводит к перемещению ее ДН в пространстве по углу q (происходит электронное сканирование ДН) в сторону уменьшения фазы на антенне, при этом главный лепесток ДН расширяется. При  главный максимум ДН ориентирован вдоль оси антенны. КНД антенны достигает максимума при оптимальном коэффициенте замедления
главный максимум ДН ориентирован вдоль оси антенны. КНД антенны достигает максимума при оптимальном коэффициенте замедления  .
.
5. Квадратичное фазовое распределение возбуждения на раскрыве апертурной антенны приводит к расширению главного лепестка ее ДН, росту боковых лепестков и пропаданию нулей между лепестками ДН.
6. Кубическое фазовое распределение возбуждения на раскрыве апертурной антенны приводит к перемещению ее ДН по углу q в сторону уменьшения фазы возбуждающего поля на раскрыве и росту боковых лепестков ДН.
Более детально влияние волновых размеров и амплитудно-фазового
распределения возбуждения на направленные свойства апертурных антенн
изучается в процессе выполнения плановой лабораторной работы.
2.1.5. Направленные свойства апертурных антенн
Большинство апертурных антенн (зеркальные, волноводно-рупорные, линзовые) имеют излучающий раскрыв плоской формы (излучающую поверхность произвольной формы). Форма контура апертуры может быть произвольной и зависит от требований, предъявляемых к виду главного лепестка ДН антенны. Для получения главного лепестка ДН апертурной антенны веерного типа обычно используют раскрывы прямоугольной (или близкой к ней) формы, для получения игольчатой ДН - круглой формы. У большинства апертурных антенн (в основном сантиметрового и миллиметрового диапазонов электромагнитных волн), как правило, площадь раскрыва  >>
>>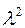 , что обеспечивает высокую направленность таких антенн.
, что обеспечивает высокую направленность таких антенн.
Вектор напряженности результирующего поля излучения апертурной антенны (в точке наблюдения В дальней зоны), как систем идентичных и одинаково ориентированных источников Гюйгенса с заданным на ее раскрыве амплитудно-фазовым распределением возбуждения (АФР), определяется выражением
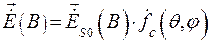 , (2.4)
, (2.4)
где  - вектор напряженности поля излучения центрального источника
- вектор напряженности поля излучения центрального источника
Гюйгенса в точке В дальней зоны апертурной антенны;
 - комплексным амплитудным множителем системы апертурной
- комплексным амплитудным множителем системы апертурной
антенны.
На основании (2.4), согласно правилу перемножения диаграмм направленности (правила Бонч-Бруевича), выражение для комплексной результирующей диаграммы направленности апертурной антенны с излучающим раскрывов произвольной формы имеет вид
 , (2.5)
, (2.5)
где  - амплитудная диаграмма направленности источника
- амплитудная диаграмма направленности источника
Гюйгенса.
Комплексный амплитудный множитель системы апертурной антенны в (2.4) и (2.5) определяется формулой

 . (2.6)
. (2.6)
где
 - функция, определяющая амплитудное распределение
- функция, определяющая амплитудное распределение
возбуждения (поля) на раскрыве антенны;
 - функция, определяющая фазовое распределение
- функция, определяющая фазовое распределение
возбуждения (поля) на раскрыве антенны.
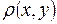 - расстояние от начала декартовой системы коорди-
- расстояние от начала декартовой системы коорди-
нат до определенного источника Гюйгенса
излучающего раскрыва площадью  ;
;
 - угол между направлением на определенный
- угол между направлением на определенный
источник Гюйгенса и направлением на точку
наблюдения (дальней зоны антенны).
При совпадении главных максимумов амплитудной ДН источника Гюйгенса и амплитудного множителя системы амплитудная ДН апертурной антенны имеет вид
 , (2.7)
, (2.7)
где  - амплитудная диаграмма направленноcти источника
- амплитудная диаграмма направленноcти источника
Гюйгенса;
 - амплитудный множитель системы апертурной антенны.
- амплитудный множитель системы апертурной антенны.
Нормированная результирующая амплитудная ДН апертурной антенны имеет вид
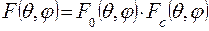 , (2.7а)
, (2.7а)
где 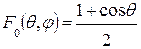 - нормированная амплитудная диаграмма
- нормированная амплитудная диаграмма
направленноcти источника Гюйгенса;
 - нормированный амплитудный множитель системы
- нормированный амплитудный множитель системы
апертурной антенны.
Нормированный амплитудный множитель системы апертурной антенны в выражении (2.7) для излучающих раскрывов различной формы имеет соответствующие выражения.
Апертурные антенны с прямоугольным излучающим раскрывом
На прямоугольных раскрывах большого размера ( >>
>> >>
>>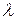 ) обычно создаются по координатам (Х, Y) разделяющиеся амплитудно-фазовые распределения (АФР) электромагнитного поля вида:
) обычно создаются по координатам (Х, Y) разделяющиеся амплитудно-фазовые распределения (АФР) электромагнитного поля вида:
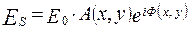 , (2.8)
, (2.8)
где:  - поле источника Гюйгенса в дальней зоне;
- поле источника Гюйгенса в дальней зоне;
 - разделяющееся амплитудное распределение
- разделяющееся амплитудное распределение
поля по сторонам прямоугольного раскрыва;
 - разделяющееся фазовое распределение поля по
- разделяющееся фазовое распределение поля по
сторонам прямоугольного раскрыва.
|
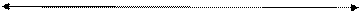


|



|
|
|
|
|
|

|
| |

 Рис. 2.8. К определению диаграммы направленности апертурной антенны с излучающим раскрывом прямоугольной формы
Рис. 2.8. К определению диаграммы направленности апертурной антенны с излучающим раскрывом прямоугольной формы
Поскольку в нашем случае:
 ,
,
то, в соответствии с (2.5), выражение для амплитудного множителя системы апертурной антенны с прямоугольным излучающим раскрывом имеет вид:
 . (2.9)
. (2.9)
Выражение (2.9) можно записать следующим образом:
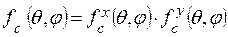 , (2.10)
, (2.10)
где: 
 ,
,

 .
.
При анализе направленных свойств апертурных антенн с прямоугольным излучающим раскрывом на практике обычно интересуются характером амплитудного множителя системы (диаграммы направленности) излучающего раскрыва с разделяющимся АФР возбуждения в главных плоскостях XOZ и YOZ.
Амплитудный множитель системы в плоскости XOZ, где  , имеет следующий вид:
, имеет следующий вид:

 , (2.11)
, (2.11)
где: 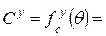
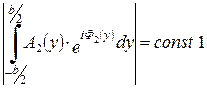 - постоянная 1.
- постоянная 1.
Нормированный амплитудный множитель системы апертурной антенны с равновозбужденным  и синфазным
и синфазным  прямоугольным излучающим раскрывом в плоскости XOZ имеет вид
прямоугольным излучающим раскрывом в плоскости XOZ имеет вид
 , (2.12)
, (2.12)
где  - приведенная угловая координата в плоскости XOZ.
- приведенная угловая координата в плоскости XOZ.
Аналогичным образом, в плоскости YOZ, где 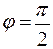 , амплитудный множитель системы записывается выражением
, амплитудный множитель системы записывается выражением

 , (2.13)
, (2.13)
где: 
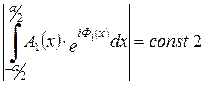 - постоянная 2
- постоянная 2
Нормированный амплитудный множитель системы апертурной антенны с равновозбужденным  и синфазным
и синфазным 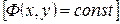 прямоугольным излучающим раскрывом в плоскости YOZ имеет вид
прямоугольным излучающим раскрывом в плоскости YOZ имеет вид
 . (2.14)
. (2.14)
где 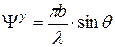 - приведенная угловая координата в плоскости YOZ.
- приведенная угловая координата в плоскости YOZ.
Учитывая тот факт, что разделяющееся амплитудно-фазовое распределение (АФР) возбуждающего прямоугольный раскрыв поля может быть различным, поэтому рассмотрим основные характеристики и параметры, определяющие направленные свойства апертурных антенн с прямоугольным излучающим раскрывом на примерах практически использующихся видах данного типа антенн:
- антенны в виде открытого конца прямоугольного волновода;
- рупорных антенн (Н и Е - плоскостных секториальных, пирамидального
рупоров);
- зеркальных антенн (антенны с зеркалом в виде прямоугольных вырезок из
параболоида вращения, параболоцилиндрической антенны).
Антенна в виде открытого конца прямоугольного волновода
Для апертурной антенны в виде открытого конца прямоугольного волновода с линейными размерами раскрыва a и b, определим характерное для данной антенны разделяющееся в основных плоскостях АФР возбуждения на излучающем раскрыве (рис. 2.9), а также основные характеристики и параметры, определяющие ее направленные свойства.
 |
Рис. 2.9. Антенна в виде открытого конца прямоугольного волновода в трехмерной системе координат
Изображение АФР возбуждения приведено на рисунке 1 приложения 4 настоящего пособия.
1. В плоскости XOZ:
косинусоидальное амплитудное распределение возбуждения 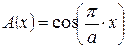 ;
;
равномерное фазовое распределение возбуждения (синфазный раскрыв)
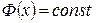 .
.
При данном АФР возбуждения нормированный амплитудный множитель системы открытого конца прямоугольного волновода рассчитывается по следующей формуле
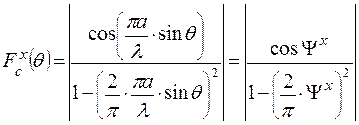 , (2.15)
, (2.15)
где  - приведенная угловая координата в плоскости XOZ;
- приведенная угловая координата в плоскости XOZ;
 - волновой размер раскрыва волновода в плоскости XOZ.
- волновой размер раскрыва волновода в плоскости XOZ.
Расчет нормированной амплитудной диаграммы направленности (ДН) антенны в виде открытого конца прямоугольного волновода, согласно (2.7а), производится по формуле
 . (2.16)
. (2.16)
Ширина нормированной амплитудной ДН по половинной мощности в данной плоскости определяется по формуле
 .
.
При практическом использовании открытого конца прямоугольного волновода в качестве самостоятельной антенны, элемента антенной решетки или облучателя зеркальной (линзовой) антенны, в расчетных данных используют приближенное значение 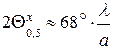 .
.
2. В плоскости YOZ:
равномерное амплитудное распределение возбуждения (равновозбужденный
раскрыв) 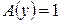 ;
;
равномерное фазовое распределение возбуждения (синфазный раскрыв)
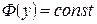 .
.
При этом нормированный амплитудный множитель системы открытого конца прямоугольного волновода рассчитывается по следующей формуле
 , (2.17)
, (2.17)
где 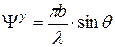 - приведенная угловая координата в плоскости YOZ;
- приведенная угловая координата в плоскости YOZ;
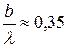 - волновой размер раскрыва волновода в плоскости XOZ.
- волновой размер раскрыва волновода в плоскости XOZ.
Расчет нормированной амплитудной диаграммы направленности (ДН) антенны в виде открытого конца прямоугольного волновода, согласно (2.7а), производится по формуле
 . (2.18)
. (2.18)
Ширина нормированной амплитудной ДН по половинной мощности в данной плоскости определяется по формуле
 .
.
Приближенное значение 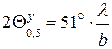 .
.
3. Максимально возможный коэффициент направленного действия (КНД) антенны в виде открытого конца прямоугольного волновода при соответствующем АФР возбуждения на излучающем раскрыве в основных плоскостях, можно представить в виде трех сомножителей
 , (2.19)
, (2.19)
где: 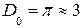 - эквивалентный КНД источника Гюйгенса;
- эквивалентный КНД источника Гюйгенса;
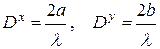 - максимальный КНД равновозбужденных
- максимальный КНД равновозбужденных
синфазных линейных антенн с размерами a и b;
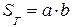 - геометрическая площадь прямоугольного излучаю
- геометрическая площадь прямоугольного излучаю
щего раскрыва;
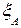 - коэффициент использования площади (КИП)
- коэффициент использования площади (КИП)
антенны в виде открытого конца прямоугольного
волновода (приближенное значение  ).
).
Н – плоскостной секториальный рупор
 |
Рассмотрим для данной антенны характерное для ее излучающего раскрыва разделяющееся в основных плоскостях АФР возбуждения (рис. 2.10), а также основные характеристики и параметры, определяющие ее направленные свойства.
Рис. 2.10. Антенна в виде в Н – плоскостного секториального рупора в
трехмерной системе координат
1. В плоскости XOZ:
косинусоидальное амплитудное распределение возбуждения  или комбинированное амплитудное распределение возбуждения
или комбинированное амплитудное распределение возбуждения 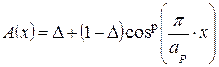 , где
, где 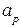 - изменяющийся размер стенки раскрыва рупора);
- изменяющийся размер стенки раскрыва рупора);
квадратичное фазовое распределение возбуждения 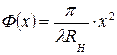 (с максимальной фазовой ошибкой
(с максимальной фазовой ошибкой  , где
, где 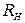 - длина рупора).
- длина рупора).
Примерное АФР возбуждения на излучающем раскрыве рупора изображено на рисунке 1 приложения 4 настоящего пособия.
Основные характеристики (амплитудную диаграмму направленности ) и параметры (максимальный КНД) в данном случае необходимо определять для оптимального Н - плоскостного секториального рупора.
Оптимальным называется такой рупор (Н и Е – плоскостные секториальные, пирамидальный и конический рупоры), который при заданном значении максимального КНД ( ) имеет наименьшую длину R (для Н – плоскостного секториального рупора -
) имеет наименьшую длину R (для Н – плоскостного секториального рупора -  ).
).
Для оптимального Н – плоскостного секториального рупора при характерном АФР возбуждения на его излучающем раскрыве в плоскости XOZ – максимальная фазовая ошибка составляет  , волновой размер
, волновой размер  и половина угла раствора рупора
и половина угла раствора рупора  .
.
Значение нормированного амплитудного множителя системы Н - плоскостного секториального рупора в плоскости XOZ  , как функция от приведенной угловой координаты
, как функция от приведенной угловой координаты  , при различных значениях
, при различных значениях 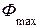 квадратичного фазового распределения возбуждения, определяется экспериментально по графику, изображенному на рисунке 1 приложения 5 настоящего пособия.
квадратичного фазового распределения возбуждения, определяется экспериментально по графику, изображенному на рисунке 1 приложения 5 настоящего пособия.
Расчет нормированной амплитудной диаграммы направленности (ДН)
Н - плоскостного секториального рупора в плоскости XOZ производится по формуле
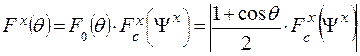 . (2.20)
. (2.20)
Диаграмма направленности непосредственно зависит от геометрических размеров рупора в данной плоскости: длины рупора  и угла раствора рупора
и угла раствора рупора  . При
. При 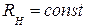 и увеличении
и увеличении  на форму ДН в плоскости XOZ воздействуют два взаимно противоположных факторов: с одной стороны – с увеличением угла раствора увеличивается размер
на форму ДН в плоскости XOZ воздействуют два взаимно противоположных факторов: с одной стороны – с увеличением угла раствора увеличивается размер 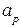 , что в свою очередь приводит к сужению ДН ; с другой стороны - увеличение размера
, что в свою очередь приводит к сужению ДН ; с другой стороны - увеличение размера 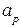 приводит к росту квадратичной фазовой ошибки
приводит к росту квадратичной фазовой ошибки 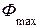 и соответственно к расширению ДН. Для устранения этого противоречия на практике данный рупор делают оптимальным.
и соответственно к расширению ДН. Для устранения этого противоречия на практике данный рупор делают оптимальным.
Ширина ДН по половинной мощности в данной плоскости определяется по формуле
 .
.
На практике для Н - плоскостного секториального рупора в расчетных данных используют приближенное значение  .
.
2. В плоскости YOZ:
АФР возбуждения на раскрыве Н - плоскостного секториального рупора в этой плоскости полностью совпадает с АФР возбуждения в плоскости YOZ антенны в виде открытого конца прямоугольного волновода: 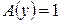 и
и 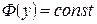 .
.
При этом нормированный амплитудный множитель системы рупора в данной плоскости также идентичен множителю системы антенны в виде открытого конца прямоугольного волновода
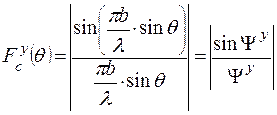 ,
,
где 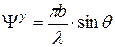 - приведенная угловая координата в плоскости YOZ;
- приведенная угловая координата в плоскости YOZ;
b - линейный размер стенки раскыва рупора, равный размеру
узкой стенки питающего прямоугольного волновода.
Аналогично можно сказать и о выражениях для расчета нормированной амплитудной диаграммы направленности (ДН) рупора и ширины ее главного лепестка по половинной мощности в плоскости YOZ
 .
.
 .
.
Приближенное значение также как и для открытого конца прямоугольного волновода составляет  .
.
3. Максимальный КНД Н - плоскостного секториального рупора определяется по формуле
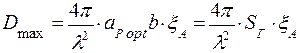 , (2.21)
, (2.21)
где: 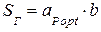 - геометрическая площадь излучающего раскрыва
- геометрическая площадь излучающего раскрыва
рупора;
 - коэффициент использования площади (КИП)
- коэффициент использования площади (КИП)
рупора (приближенное значение  ).
).
Е – плоскостной секториальный рупор
Рассмотрение АФР возбуждения и направленных свойств данной рупорной антенны проведем по аналогичной методике, как и в случае Н – плоскостного секториального рупора (рис. 2.11). Расчет нормированной амплитудной ДН, ее параметров и значения максимальный КНД в данном случае необходимо определять для оптимального Е - плоскостного секториального рупора.
Вид АФР возбуждения на излучающем раскрыве в основных плоскостях изображен на рисунке 1 приложения 4 настоящего пособия.
|
|


Рис. 2.11. Антенна в виде в Е– плоскостного секториального рупора в
трехмерной системе координат
1. В плоскости XOZ:
АФР возбуждения на раскрыве Е - плоскостного секториального рупора в этой плоскости полностью совпадает с АФР возбуждения в плоскости ХOZ антенны в виде открытого конца прямоугольного волновода:
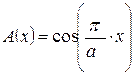 или
или 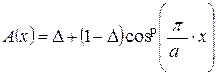 , где
, где  - размер стенки раскрыва рупора в плоскости XOZ, равный размеру широкой стенки питающего прямоугольного волновода;
- размер стенки раскрыва рупора в плоскости XOZ, равный размеру широкой стенки питающего прямоугольного волновода;
 .
.
Выражение для нормированного амплитудный множителя системы рупора в данной плоскости совпадает с выражением для множителя системы антенны в виде открытого конца прямоугольного волновода
 ,
,
где  - приведенная угловая координата в плоскости XOZ.
- приведенная угловая координата в плоскости XOZ.
Аналогично можно сказать и о выражениях для расчета нормированной амплитудной диаграммы направленности (ДН) рупора и ширины ее главного лепестка по половинной мощности в плоскости YOZ
 .
.

. Приближенное значение 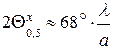 .
.
2. В плоскости YOZ:
АФР возбуждения на излучающем раскрыве Е - плоскостного секториального рупора в этой плоскости следующее:
- амплитудное распределение возбуждения - равномерное 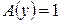 ;
;
- фазовое распределение возбуждения - квадратичное 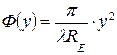 (с макси-
(с макси-
мальной фазовой ошибкой  , где
, где  - изменяющийся размер стенки рупора,
- изменяющийся размер стенки рупора,  - длина рупора).
- длина рупора).
Для оптимального Е – плоскостного секториального рупора при указанном АФР возбуждения на его излучающем раскрыве в плоскости YOZ – максимальная квадратичная фазовая ошибка составляет  , волновой размер
, волновой размер  и половина угла раствора рупора
и половина угла раствора рупора  .
.
Величину нормированного амплитудного множителя системы Е - плоскостного секториального рупора в плоскости YOZ 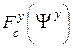 , как функция от приведенной угловой координаты
, как функция от приведенной угловой координаты  , при различных значениях максимальной квадратичной фазовой ошибке
, при различных значениях максимальной квадратичной фазовой ошибке 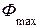 определяется по экспериментальному графику, изображенному на рисунке 2 приложения 5 настоящего пособия.
определяется по экспериментальному графику, изображенному на рисунке 2 приложения 5 настоящего пособия.
Нормированная амплитудная ДН E - плоскостного секториального рупора в плоскости YOZ рассчитывается по формуле
 . (2.22)
. (2.22)
По аналогии, как и в случае Н - плоскостного секториального рупора, форма диаграммы направленности рассматриваемой антенны непосредственно зависит от геометрических размеров рупора в плоскости YOZ (в частности от длины рупора 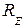 и угла раствора рупора
и угла раствора рупора  ) и возникающие при этом противоречия в определении ее параметров. Поэтому в практических целях геометрические размеры E - плоскостной секториальный рупор также оптимизируют.
) и возникающие при этом противоречия в определении ее параметров. Поэтому в практических целях геометрические размеры E - плоскостной секториальный рупор также оптимизируют.
Ширина ДН рупора по половинной мощности в рассматриваемой плоскости определяется по формуле
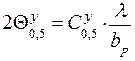 .
.
На практике для данной рупорной антенны в расчетных данных используют приближенное значение  .
.
3. Максимальный КНД Е - плоскостного секториального рупорной антенны определяется по формуле
 , (2.23)
, (2.23)
где:  - геометрическая площадь излучающего раскрыва
- геометрическая площадь излучающего раскрыва
рупора;
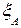 - коэффициент использования площади (КИП)
- коэффициент использования площади (КИП)
рупора (приближенное значение  ).
).
Пирамидальный рупор
Пирамидальный рупор конструктивно образован одновременным плавным увеличением линейных размеров широкой и узкой стенок питающего прямоугольного волновода, и является комбинацией Н и Е – плоскостных секториальных рупорных антенн (рис. 2.12). Анализ АФР возбуждения и направленных свойств пирамидального рупора производится по аналогичной методике, как и анализе направленных свойств плоскостных секториальных рупоров с прямоугольными излучающими раскрывами. Определение основных характеристик и параметров также необходимо производить при оптимизации пирамидального рупора. Вид АФР возбуждения на прямоугольном излучающем раскрыве пирамидального рупора в основных плоскостях изображен на рисунке 1 приложения 4 настоящего пособия.
|
|


Рис. 2.12. Антенна в виде в пирамидального рупора в трехмерной системе координат
Вид АФР возбуждения на прямоугольном излучающем раскрыве пирамидального рупора в основных плоскостях изображен на рисунке 1 приложения 5 настоящего пособия.
1. В плоскости XOZ:
АФР возбуждения на раскрыве пирамидального рупора в этой плоскости полностью идентично с АФР возбуждения в плоскости ХOZ Н – плоскостного секториального рупора, а именно.:
косинусоидальное  или комбинированное
или комбинированное 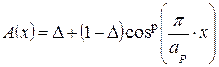 амплитудное распределение возбуждения,
амплитудное распределение возбуждения,
где 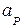 - размер излучающего раскрыва рупора в плоскости XOZ;
- размер излучающего раскрыва рупора в плоскости XOZ;
квадратичное фазовое распределение возбуждения 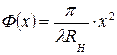 (с макси-
(с макси-
мальной фазовой ошибкой  , где
, где 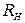 - длина пирамидального рупора в плоскости ХOZ).
- длина пирамидального рупора в плоскости ХOZ).
Выражения для определения геометрических размеров оптимального пирамидального рупора аналогичны, как и для оптимального Н – плоскостного секториального рупора в плоскости XOZ – максимальная фазовая ошибка составляет  , волновой размер
, волновой размер  и половина угла раствора рупора
и половина угла раствора рупора  .
.
Значение нормированного амплитудного множителя системы пирамидального рупора в плоскости XOZ  , как функция от приведенной угловой координаты
, как функция от приведенной угловой координаты  , при различных значениях
, при различных значениях 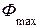 квадратичного фазового распределения возбуждения, определяется экспериментально по графику, изображенному на рисунке 1 приложения 5 настоящего пособия.
квадратичного фазового распределения возбуждения, определяется экспериментально по графику, изображенному на рисунке 1 приложения 5 настоящего пособия.
Нормированная амплитудная диаграмма направленности (ДН)
пирамидального рупора в плоскости XOZ рассчитывается по формуле
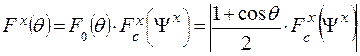 . (2.24)
. (2.24)
Аналогично, как в случае Н – плоскостного секториального рупора) форма диаграммы направленности непосредственно зависит от геометрических размеров рупора в данной плоскости: длины рупора  и угла раствора рупора
и угла раствора рупора  .
.
В практических целях геометрические размеры пирамидального рупор в данной плоскости оптимизируют.
Ширина главного лепестка ДН по половинной мощности в данной плоскости определяется по формуле
 .
.
На практике используют приближенное значение  .
.
2. В плоскости YOZ:
АФР возбуждения на излучающем раскрыве пирамидального рупора идентично АФР возбуждения Е - плоскостного секториального рупора в плоскости YOZ :
- амплитудное распределение возбуждения - равномерное 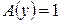 ;
;
- фазовое распределение возбуждения - квадратичное 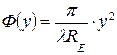 (с максимальной фазовой ошибкой
(с максимальной фазовой ошибкой  , где
, где  - размер излучающего раскрыва рупора в плоскости XOZ и
- размер излучающего раскрыва рупора в плоскости XOZ и  - длина рупора в плоскости YOZ).
- длина рупора в плоскости YOZ).
Для оптимального пирамидального рупора, как и для Е - плоскостного секториального рупора в плоскости YOZ – максимальная квадратичная фазовая ошибка составляет  , волновой размер
, волновой размер  и половина угла раствора рупора
и половина угла раствора рупора  .
.
Величину нормированного амплитудного множителя системы пирамидального рупора в плоскости YOZ 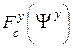 , как функция от приведенной угловой координаты
, как функция от приведенной угловой координаты  , при различных значениях максимальной квадратичной фазовой ошибки
, при различных значениях максимальной квадратичной фазовой ошибки 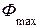 определяется по экспериментальному графику, изображенному на рисунке 2 приложения 5 настоящего пособия.
определяется по экспериментальному графику, изображенному на рисунке 2 приложения 5 настоящего пособия.
Нормированная амплитудная ДН пирамидального рупора в плоскости YOZ рассчитывается по формуле
 . (2.25)
. (2.25)
По аналогии, как и в случае Е - плоскостного секториального рупора, форма диаграммы направленности пирамидального рупора непосредственно зависит от геометрических размеров рупора в плоскости YOZ (в частности от длины рупора 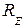 и угла раствора рупора
и угла раствора рупора  ) и возникающие при этом противоречия в определении ее параметров. Поэтому в практических целях геометрические размеры пирамидального рупора и в этой плоскости также оптимизируют.
) и возникающие при этом противоречия в определении ее параметров. Поэтому в практических целях геометрические размеры пирамидального рупора и в этой плоскости также оптимизируют.
Ширина ДН рупора по половинной мощности в рассматриваемой плоскости определяется по формуле
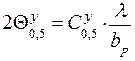 .
.
На практике для данной рупорной антенны в расчетных данных используют приближенное значение 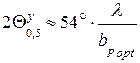 .
.
3. Коэффициент направленного действия (КНД) пирамидальной рупорной антенны можно определить по выражению
 , (2.26)
, (2.26)
где 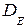 ,
, 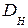 - КНД Е и Н –плоскостных секториальных рупорных антенн
- КНД Е и Н –плоскостных секториальных рупорных антенн
соответственно;
Максимальный КНД оптимальной пирамидальной рупорной антенны определяется при полном равенстве длин рупора в основных плоскостях 
 , (2.27)
, (2.27)
где 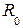 - усредненное значение длины рупора в плоскостях XOZ и YOZ.
- усредненное значение длины рупора в плоскостях XOZ и YOZ.
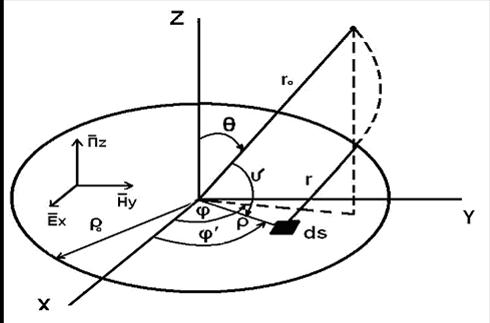
Апертурные антенны с круглым излучающим раскрывом
|
|
 H1.
H1.
Рис. 2.13. К определению амплитудной диаграммы направленности апертурной антенны с излучающим раскрывом круглой формы
Учитывая, что в случае круглого раскрыва с конкретным АФР возбуждения в выражении (2,6)

значение амплитудного множителя системы имеет вид
 . (2.28)
. (2.28)
В большинстве случаев амплитудное распределение возбуждающего поля на круглом раскрыве осесимметричное (т.е. не зависит от координаты 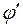 ) и спадающее к его краям. Выражение для такого амплитудного распределения, как правило, имеет вид
) и спадающее к его краям. Выражение для такого амплитудного распределения, как правило, имеет вид
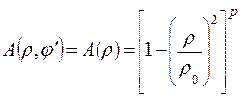 , (2.29)
, (2.29)
где: р = 0, 1, 2,… - степень спада амплитудного распределения к краям
круглого раскрыва;
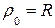 - радиус круглого излучающего раскрыва.
- радиус круглого излучающего раскрыва.
Нормированный амплитудный множитель системы круглого излучающего раскрыва имеет вид
 , (2.30)
, (2.30)
где:  - лямбда-функция (р+1)-го порядка, зависящая от
- лямбда-функция (р+1)-го порядка, зависящая от
«аргумента» 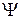 ;
;
 - приведенная угловая координат;
- приведенная угловая координат;
 - волновое число.
- волновое число.
График функции 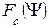 синфазного круглого излучающего раскрыва при степени спада р=0 и р=1 приведен на рисунке 1 приложения 4 настоящего учебного пособия.
синфазного круглого излучающего раскрыва при степени спада р=0 и р=1 приведен на рисунке 1 приложения 4 настоящего учебного пособия.
Полагая, что на излучающем раскрыве амплитудное распределение возбуждения имеет вид (2.29) и фазовое распределение возбуждения равномерное  (синфазный раскрыв), находим выражения для нормированной амплитудной ДН апертурной антенны с круглым излучающим раскрывом в основных плоскостях:
(синфазный раскрыв), находим выражения для нормированной амплитудной ДН апертурной антенны с круглым излучающим раскрывом в основных плоскостях:
в плоскости ХOZ<
– Конец работы –
Эта тема принадлежит разделу:
АНТЕННЫ И РАСПРОСТРАНЕНИЕ РАДИОВОЛН
МИНИСТЕРСТВА ТРАНСПОРТА И КОММУНИКАЦИЙ... РЕСПУБЛИКИ БЕЛАРУСЬ... Минский государственный высший авиационный колледж...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Основные закономерности в антеннах
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов