рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Последовательность действий, выполняемая при моделировании в CAE-системах, использующих МЭК.
Реферат Курсовая Конспект
Последовательность действий, выполняемая при моделировании в CAE-системах, использующих МЭК.
Последовательность действий, выполняемая при моделировании в CAE-системах, использующих МЭК. - раздел Философия, МОДЕЛИРОВАНИЕ ОБЪЕКТОВ В МЕТАЛЛУРГИИ Практическая Реализация Мкэ В Программных Продуктах Обычно Осуществляется В С...
Практическая реализация МКЭ в программных продуктах обычно осуществляется в следующем порядке:
- Создание геометрической модели и ее дискретизация.
- Задание типа КЭ.
- Создание сетки КЭ.
- Задание граничных условий.
- Задание свойств материала.
- Выбор параметров расчета.
- Осуществление расчета (автоматически).
- Анализ полученных результатов.
2.3 Создание геометрической модели и ее дискретизация.
Для решения любой задачи ОМД на компьютере необходимо, прежде всего, создать геометрическую модель, описывающую пространственные характеристики моделируемого объекта.
2.3.1 Создание геометрической модели
Геометрическая модель - математическое представление геометрической формы, хранимое в памяти компьютера. Различают двухмерные (2D-модели) и трехмерные (3D-модели) модели. Аналогично подразделяются и системы, обеспечивающие плоское и объемное проектирование. Как правило, современные 3D-системы проектирования имеют встроенные 2D-системы, необходимые для изготовления плоских чертежей /15, 20/.
Элементы, из которых состоит трехмерная модель, образуют в ней вершины, ребра, грани (рис. 13) /21, 23-25/.
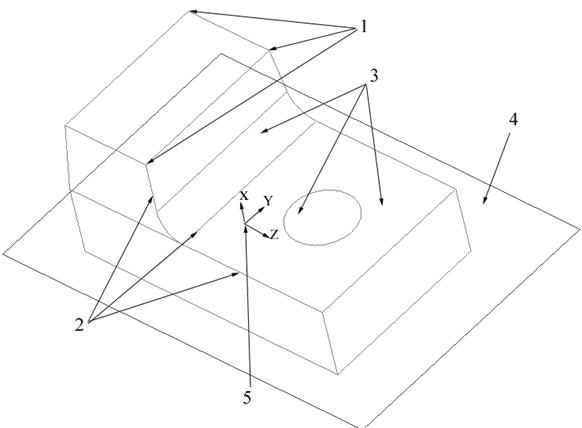
Рисунок 13 – Элементы трехмерной модели: 1 – вершины; 2 – грани;
3 – поверхности; 4 – базовая плоскость; 5 – начало координат
Вершина – точка являющаяся окончанием (началом) ребра.
Ребро – прямая или кривая, разделяющая две смежные грани модели.
Грань – гладкая часть поверхности модели. Гладкая поверхность модели может состоять из нескольких граней.
Методы трехмерного моделирования, предоставляемые системами САПР, делятся на три категории: каркасное, поверхностное (полигональное) и твердотельное (сплошное) моделирование /15/.
2.3.1.1 Каркасное моделирование
Процесс каркасного моделирования является моделированием самого низкого уровня. Каркасная модель полностью описывается с помощью линий и точек и поэтому требует гораздо меньше компьютерной памяти, чем остальные модели, и пригодна для решения наиболее простых задач. Каркасное моделирование широко используется для имитации траектории движения инструмента, выполняющего несложные операции обработки детали.
Каркасные модели имеют больше количество ограничений, рассмотрим их более подробно /15/.
2.3.1.2 Ограничения каркасных моделей
· Неоднозначность. Серьезным недостатком рассматриваемых моделей является сложность зрительного восприятия видимого изображения на экране монитора. Например, на рисунке 14 трехмерное изображение можно интерпретировать и как вид сверху (рис. 14б), и как вид снизу (рис. 14в), что сильно усложняет работу конструктора. В отличие от твердотельной модели в каркасной модели нельзя отличить "видимые" грани геометрической формы от "скрытых" (невидимых).
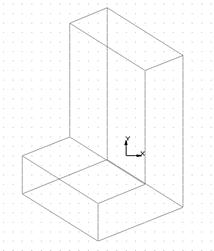 а)
а)
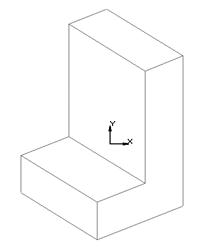 б)
б) 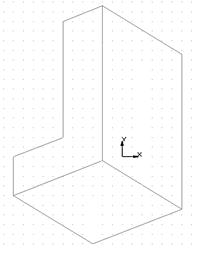 в)
в)
Рисунок 14 – Неоднозначность каркасной модели
· Невозможность распознавания криволинейных поверхностей. Боковые поверхности цилиндрических тел не имеют ребер, хотя на изображении видно силуэты мнимых ребер, которые ограничивают поверхности. Расположение этих "ребер" в пространстве меняется в зависимости от направления вида (точки зрения), поэтому такие силуэты не являются элементами каркасной модели.
На рисунке 15 показано трехмерное изображение твердотельной и каркасной моделей. Видимые на рисунке 15а мнимые “ребра” отсутствуют на главном виде (рис. 15б) и на видах сверху (рис. 15в) и справа (рис. 15г)
Мнимые “ребра”
 а)
а)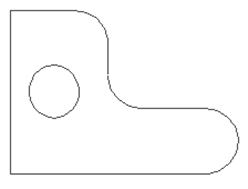 б)
б) в)
в) г)
г)
Рисунок 15 – Мнимые ребра каркасной модели
· Невозможность обнаружения взаимного влияния компонентов. Каркасная модель не несет информацию о поверхностях ее ограничивающих, поэтому при использовании такой модели нет возможности обнаружить нежелательные взаимодействия между поверхностями объекта. Это является наиболее существенным ограничением применения каркасного моделирования при трехмерном геометрическом моделировании сборочных узлов и конструкций таких, как например штамповая оснастка.
· Трудности вычисления физических характеристик. Правильно построенная геометрическая форма, (объем тела), отличается от стандартных базовых компонентов, поэтому физические характеристики могут быть определены неточно. Таким образом, значения физических характеристик (например, масса, площадь поверхности, центр тяжести или моменты инерции) будут недостоверными.
2.3.1.3 Поверхностное моделирование
Поверхностная модель определяется с помощью точек, линий и поверхностей, поэтому ее можно рассматривать как модель более высокого уровня.
Поверхностное моделирование дает следующие преимущества по сравнению с каркасным /15/:
- способность распознавать и изображать сложные криволинейные поверхности,
- способность распознавать грани и таким образом обеспечивать средство получения тоновых трехмерных изображений;
- способность распознавать особые построения на поверхностях, например, отверстия;
- возможность получения более качественного, чем при каркасном моделировании изображения.
Поскольку в ходе поверхностного моделирования мы имеем дело в основном с поверхностями, то ниже будут рассмотрены основные виды плоскостей и способы их получения.
2.3.1.4 Основные виды поверхностей, используемые при моделировании.
Применительно к поверхностному моделированию можно выделить следующие типы поверхностей /15/:
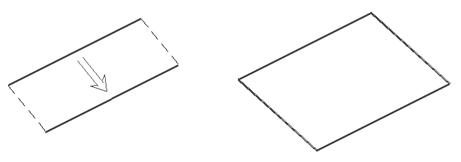
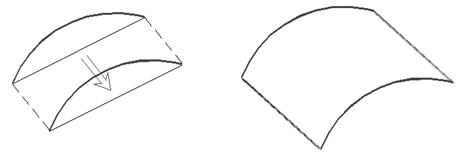
· Кинематические поверхности. Это поверхности, которые можно получить, движением отрезка прямой в указанном направлении на заданную величину (рис. 16а) или по другому отрезку. Полученную в первом случае поверхность называют поверхностью выдавливания, а во втором - кинематической поверхностью. Заменив отрезок прямой на дугу, можно получить цилиндрическую поверхность (рис. 16б).
 а)
а)
 б)
б)
Рисунок 16 – Построение базовых геометрических поверхностей
Особенностью систем поверхностного моделирования является то, что они не распознают такие построения, как твердые объемные тела. Они представляют такие объекты, как поверхности, соединенные друг с другом в пространстве и ограничивающие "пустой" объем.
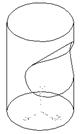
На рисунке 17 показана кинематическая поверхностная модель, которая на экране представлена виде объемного тела, в то время как в компьютерном представлении модель состоит из пяти поверхностей.

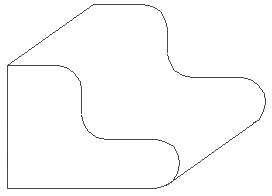
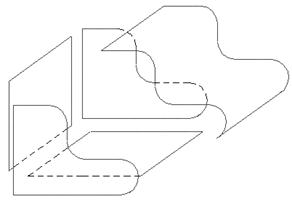
Рисунок 17 – Визуальное и компьютерное представление поверхностной модели
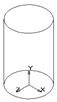
· Поверхности вращения могут быть получены по команде, создающей поверхность вращением плоского контура вокруг определенной оси. При этом необходимо помнить, что создается не объемное тело, а генерируется только поверхность (рис. 18).
· Поверхности сопряжений и пересечений. Такие поверхности получаются при создании плавных переходов в местах соединения двух различных по форме элементов. Возможность построения плавного сопряжения одной поверхности с другой является наиболее мощными часто используемым на практике средством поверхностного моделирования.
На рисунке 19 показаны поверхности сопряжения (внешняя и внутренняя) построенные на пересечении двух элементов детали (поверхность сопряжения - радиусный участок детали в переходе от основного участка трубы к ответвлению).
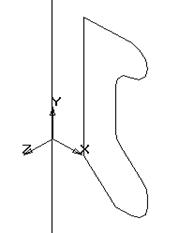
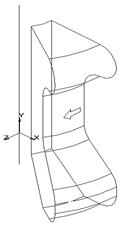
Рисунок 18 – Создание поверхности вращения
 а)
а) 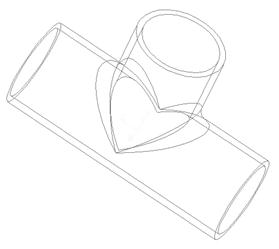 б)
б)
Рисунок 19– Поверхности сопряжения
· Аналитические поверхности. Каждая такая поверхность определяется одним математическим уравнением с неизвестными X, Y, Z (эти неизвестные обозначают искомые координаты поверхности в координатном пространстве). Для изображения аналитической поверхности, необходимо знать математическое уравнение, которым оно описывается.
· Скульптурные поверхности (поверхности "свободных форм" или "произвольные" поверхности) нельзя описать одним математическим уравнением. В большинстве случаев образы этих поверхностей создаются путем построения кривых продольных образующих между точками, определенными в трехмерном пространстве (рис. 20).
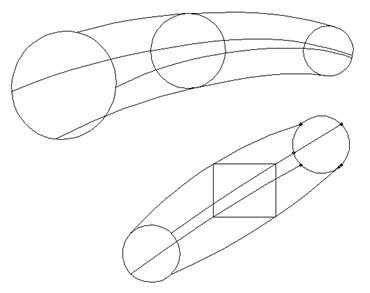
Рисунок 20 – Скульптурные поверхности
Несмотря на то, что методы поверхностного моделирования обладают многими достоинствами, существует ряд ограничений на их использование. К подобным ограничениям можно отнести:
- возникновение неоднозначности при попытке моделирования реального твердого тела;
- недостаточная точность представления некоторых поверхностных моделей для обеспечения надежных данных о трехмерных объемных телах;
- сложность процедур удаления скрытых линий и отображения внутренних областей.
2.3.1.5 Твердотельное моделирование
Твердотельная модель описывается в терминах того трехмерного объема, который занимает определяемое ею тело. Твердотельное моделирование дает полное однозначное описание трехмерной геометрической формы.
Достоинством твердотельных моделей являются /15/:
· полное определение объемной формы с возможностью разграничения внешней и внутренней областей объекта, что позволяет обнаружить нежелательные взаимовлияния компонентов;
· обеспечение автоматического удаления скрытых линий;
· автоматическое построение трехмерных разрезов компонентов, что особенно важно при анализе сложных деталей и сборочных изделий;
· получение точных весовых характеристик детали.
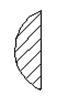
Как правило, в основе трехмерных моделей лежит математический аппарат алгебраической теории множеств, использующий в своей основе булевы операции. Рассмотрим в качестве примера три булевы операции: объединение, разность и пересечение (рис. 21).
Операция объединения. Результатом операции является одно тело, объединяющее исходные тела. Объединение двух произвольных фигур показано на рисунке 21б (заштрихованная область).
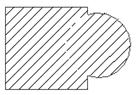
Операция разности. Результатом выполнения операции является фигура, находящаяся внутри границ ограниченных поверхностью, оставшейся от одной формы, и внешней границей общей области двух форм. На рисунке 21в заштрихованной областью показан результат действия операции булевой разности.
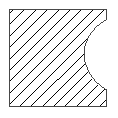
Операция пересечения. Результатом является фигура, находящаяся внутри границ общей области объектов. Пересечение фигур представлено на рисунке 21г заштрихованной областью.
Как при поверхностном моделировании, твердотельные объекты могут быть созданы с помощью тех же способов что и плоскости, только в данном случае образуется существенно "твердый объем", а не пустое пространство, ограниченное несколькими поверхностями.
| Примеры тел | Объединение | Разность | Пересечение |
 плоское
плоское
| 
| 
| 
|
  объемное
а)
объемное
а)
|  б)
б)
|  в)
в)
|  г)
г)
|
Рисунок 21 – Результаты булевых операций.
В процессе построения детали при сплошном моделировании в начале осуществляется построение основания, а затем с помощью булевых операций выполняется построение дополнительных элементов.
2.3.1.6 Понятие гибридного моделирования
Возможность свободного создания и изменения различных объектов вне зависимости от того, каким образом в математическом представлении описывается объект (с помощью каркасного, поверхностного или сплошного моделирования) является сильной стороной любой системы моделирования. Подобное сочетание возможностей различных методов появляется с использованием технологии гибридного моделирования. При построении в подобных системах право выбора эффективной стратегии (т.е. вид представления модели) каждого элемента одного и того же объекта принадлежит пользователю.
Обычно построение модели с помощью систем гибридного моделирования осуществляется на основе твердотельных объектов, а затем добавления элементов, построенных с помощью поверхностного моделирования (например, таким объектом могут быть скульптурные поверхности). На следующем этапе данные поверхностные элементы превращаются (часто автоматически) в твердые тела и далее к ним могут быть применены все операции характерные для работы с твердыми телами.
Геометрическая модель может быть построена как собственными средствами программы инженерных расчетов (CAE-системы) так и в другой программе, специализирующейся на создании геометрических моделей, (в роли таких программ выступают CAD-системы) как правило, CAD системы имеют больше возможностей для геометрического моделирования. Для переноса геометрической модели из CAD системы в CAE систему используются специальные форматы (STL, AGES, и др.).
Построенная геометрическая модель, как правило, является непрерывной и определяется либо с помощью сплошного объекта либо с помощью поверхностей. Такая модель для использования в расчетах должна быть дискретизирована. Процесс дискретизации непрерывной модели может быть сведен к двум этапам:
На первом этапе осуществляется выбор КЭ, с помощью которых будет описываться геометрическая модель.
На втором – объединение КЭ в сетку или ассамблирование с математической точки зрения процесс ассамблирования заключается в объединении матриц жесткости отдельных КЭ в глобальную матрицу жесткости всего тела. Для осуществления ассамблирования используются нумерации узлов внутри каждого КЭ и глобальная нумерация узлов. При этом между глобальной и локальной нумерацией узлов существует однозначное соответствие. Можно ли осуществлять сразу построение дискретной модели? Можно, но этот процесс применяется редко из-за его сложности.
2.4 Задание типа КЭ
Как отмечалось ранее основой для решения задач с помощью МКЭ является замена сплошного тела математической моделью, которая состоит из непересекающихся более простых КЭ.
Каждый КЭ описывается с помощью значений сплошной функции в узлах КЭ (степеней свободы). Поведение математической модели в целом зависит от поведения отдельных КЭ и их объединения в дискретную модель /14,16/.
Рассмотрим свойства (атрибуты) КЭ.
В зависимости от размерности исследуемой задачи и принимаемых допущений КЭ можно представить в виде /14, 16/:
· Одномерных элементов, имеющих форму линии, которые используются для описания поведения таких конструктивных элементов как стержни, балки и т.д. В задачах ОМД практически не используются, (рис. 22а).
 а)
а) б)
б)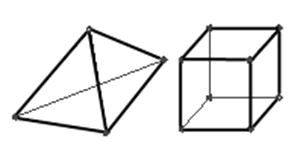 в)
в)
Рисунок 22 – типы КЭ в зависимости от размерности:
а – одномерные; б – двумерные; в – трехмерные
· Двухмерных элементов, имеющих треугольную или четырехугольную формы. Используются для описания плоских тел, у которых одно измерение значительно меньше двух других. Применяются для описания деформируемых тел листовой штамповки или для описания задач, которые можно упростить до уровня расчета в плоскости (рис. 22б).
· Трехмерных элементов, имеющих форму тетраэдров и гексаэдров. Используются для описания объемных тел, при описании большинства задач ОМД (рис. 22в).
Показанные на рисунке 22 элементы имеют прямолинейные ребра и описываются линейной функцией формы, поэтому не всегда достаточно точно описывают особенности поведения исследуемой функции. На рисунке 23 показана функция перемещений КЭ при заполнении радиусного участка гравюры штампа. Плоское ребро “мешает” точно описать геометрию штампа. Поэтому для описания апроксемирующей функции элемента (функции формы) используют полиномы более высоких степеней второй или третьей.
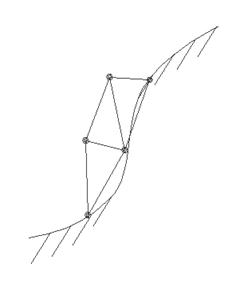
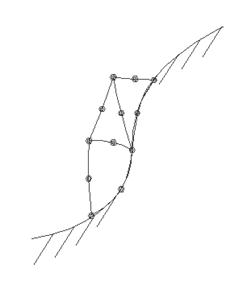
Рисунок 23 – Замена гравюры штампа на конечные элементы:
а – линейными КЭ; б – квадратичными КЭ.
Таким образом, в зависимости от используемой функции формы КЭ делятся на:
· Линейные, которые описываются полиномом 1 степени, при этом ребро образовано двумя узлами (рис. 24а).
· Квадратичные, которые описываются полиномом 2 степени, ребро образовано тремя узлами (рис. 24б).
· Кубические, которые описываются полиномом 3 степени, ребро образовано четырьмя узлами (рис. 24в).
 а)
а) б)
б) в)
в)
Рисунок 24 – Типы конечных элементов в зависимости от используемой функции формы: а – линейные; б – квадратичные; в – кубические
По расположению узловых точек элемента бывают обычные и вырожденные элементы. Вырожденные элементы это элементы, которые вследствие дискретизации приняли такую форму, у которой часть узлов совпала. Возникают такие элементы, как правило, в местах перехода от более крупной сетки к более мелкой и могут служить источниками неоднозначности и ошибок расчетов /14/.
Каждый КЭ обладает конечным количеством степеней свободы, которые определяют состояние элемента или физическое поле, которое описывает данный элемент. За счет общих степеней свободы в узлах соседних элементов осуществляется объединение КЭ в дискретную модель.
Каждый элемент обладает свойством материала. При описании свойств материала используются различные модели, рассмотренные ниже.
В зависимости от вида приложения (программы) и решаемых в нем задач могут использоваться различные типы КЭ. В ряде случаев КЭ могут содержать свойства нескольких более простых КЭ. Такие элементы называют макроэлементами, они позволяют описывать поведение текстурированных и композиционных материалов.
2.5 Создание сетки КЭ (ассамблирование).
Важным этапом моделирования с помощью МКЭ является дискретизация или построение сетки конечных элементов КЭ. Обычно в современных программных продуктах реализуется несколько вариантов построения сетки КЭ (в дальнейшем просто сетки). Поскольку увеличение возможностей создания сетки дает инженеру, использующему программу, более гибкий инструмент для решения более широкого класса задач.
В современных программах широкое применение нашло два направления, связанных с построением сетки. Это явное и неявное моделирования. При осуществлении процесса явного моделирования пользователь должен полностью определить параметры сетки КЭ и ее локальные особенности. Для осуществления подобной работы программа должна быть оснащена значительными средствами, позволяющими редактировать отдельные фрагменты и всю сетку в целом. Использование этих средств базируется на знании пользователем МКЭ, поэтому данное направление требует более высокой квалификации пользователя.
В случае использования неявного моделирования работа с построением сетки ограничивается заданием величины ребра КЭ или количеством КЭ. Обычно, программы сочетают оба направления моделирования тем самым, позволяя пользователю быстро создать сетку и при необходимости ее отредактировать.
Практически все программные продукты в настоящий момент имеют автоматический генератор сетки, который может создавать сетку автоматически после указания количества КЭ, либо по заданной пользователем величине ребра КЭ. При этом сетка может быть как упорядоченной (когда КЭ обладают определенной формой и размерами в близи друг друга) или произвольной, свободной (при этом размеры соседних КЭ могут значительно отличаться друг от друга).
Очевидна взаимосвязь между количеством КЭ в сетке и их размерами: количество КЭ в модели определяет их размеры и наоборот размер КЭ определяет их количество в сетке.
Согласно рекомендациям /14/ при выборе КЭ для сетки необходимо учитывать то что:
· линейные элементы требуют более частой сетки, чем квадратичные (с одним промежуточным узлом) или кубические (с двумя промежуточными узлами);
· упорядоченная сетка является более предпочтительной, чем произвольная;
· прямоугольная сетка с 4 узлами более предпочтительна, чем сетка с треугольными элементами;
· сетка прямоугольных элементов с промежуточными узлами имеет ту же точность, что и сетка прямоугольных элементов с 4 узлами;
· прямоугольная сетка с 8 узлами является более предпочтительной, чем сетка треугольных элементов с промежуточными узлами, несмотря на большой размер прямоугольных элементов; аппроксимация смещений кубическим полиномом не требует более мелкой сетки.
Поскольку точность расчета напрямую зависит от того, какие размеры имеет КЭ, то необходимо придерживаться следующих рекомендаций:
В тех местах, где ожидаются большие величины напряжений деформаций необходимо, чтобы сетка была более плотной, обычно такие места на заготовке соответствуют концентраторам напряжений на инструменте.
С другой стороны в местах, где не ожидается интенсивное течение металла и больших давлений сетка может иметь большие размеры КЭ.
В соответствие с требованиями /17/ при построении сетки для корректного описания геометрической модели размеры КЭ сетки должны быть минимум в три раза меньше чем наименьший концентратор напряжений на данном участке. Данное требование создает необходимость строить сетки с большим количеством КЭ при наличии небольших концентраторов напряжений, что значительно усложняет моделирование процессов листовой штамповки, где для дискретизации при объемном решении задачи по толщине заготовки необходимо строить более трех элементов при значительной поверхности заготовки.
При моделировании задач с объемным напряженным состоянием, например, пробивки (вырубки) или чеканки количество КЭ в сетки можно уменьшить введением локального сгущения сетки /17, 18/. При этом сгущение сетки должно быть осуществлено таким образом, чтобы размеры соседних конечных элементов не превышали друг друга более чем в два раза /14/.
На точность расчета влияет также форма КЭ. Так нежелательно использовать в сетке конечные элементы, имеющие один из размеров значительно больше и меньше других размеров /14/.
Очевидно, также и то, что чем больше число КЭ в сетке, тем дольше ЭВМ будет осуществлять вычисления. При этом с ростом числа КЭ будет расти и погрешность вычисления, связанная с погрешностью округления результатов расчета на ЭВМ. С другой стороны грубое описание исходной геометрической модели крупной сеткой тоже создает значительные ошибки. Следовательно, ошибка вычисления всегда будет присутствовать независимо от размера КЭ (рис. 25).
С другой стороны грубая сетка дает заниженный на 20-40% результат рассчитанных напряжений, что необходимо учитывать /22/.
Обычно при моделировании с помощью МКЭ поступают в соответствии с методом последовательного приближения: сначала осуществляют расчет на более грубой сетке, т.е. сетке с малым количеством КЭ, затем, получив предварительные расчеты, увеличивают количество конечных элементов и рассчитывают задачу снова, полученные данные анализируют, если разница, полученная в результате двух последних расчетов отличается менее чем на устраивающую исследователя погрешность, то для анализа результатов моделирования используют вариант с последней рассчитываемой сеткой.
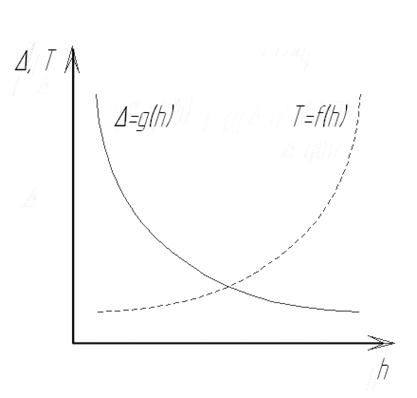
Рисунок 25 – Иллюстрация к погрешности вычисления с помощью МКЭ:
Δ – ошибка; T – время расчета; h – размер ребра КЭ, применяемого для расчета
2.6 Задание граничных условий
Граничные условия, используемые в моделировании можно разделить на два типа: искусственные и естественные. Естественные граничные условия накладываются на искомую функцию, в то время как искусственные на ее производные. Естественные граничные условия появляются при работе с исходной математической моделью.
С точки зрения МКЭ искусственные граничные условия – это граничные условия, влияющие непосредственно на степени свободы модели, и являются искусственным ограничением для перемещения. При этом ограничения могут быть наложены в одном, двух или трех направлениях на узлы сетки. В теории упругости эти ограничения называются также кинематическими. Примером в ОМД может быть ограничение течения металла через рабочую поверхность штампа. Ограничение создаётся автоматически программой расчета.
Естественные граничные условия накладываются на вектор усилий напряжений. К этим условиям относят различные внешние силовые воздействия, действующие на точки или поверхности тела. Обычно такие граничные условия называют силовыми граничными условиями. Примером в ОМД могут быть силовые условия деформирования металла.
На практике приходится сталкиваться еще и со смешанными граничными условиями. В этом случае в данной точке поверхности тела задаются напряжения и перемещения. Наиболее распространенный пример таких граничных условий это задание плоскостей геометрической симметрии при решении задач деформирования осесимметричных тел. При решении задач по деформированию тел с геометрической симметрией смешанные граничные условия заключаются в равенстве нулю нормальных перемещений и равенству нулю касательных напряжений в узлах КЭ лежащих на плоскости симметрии.
На практике задание любых граничных условий являются важным элементом моделирования. Задание граничных условий должно отвечать следующим требованиям.
· Граничные условия не должны быть абсурдны по своей сути – например, при изучении процесса прикладывать усилие и фиксировать перемещение в одном и том же направлении не имеет смысла, нет смысла также фиксировать все перемещения в узлах дискретной модели (рисунок 26).
· Должно быть соответствие действия граничных условий на реальном теле и на модели как по усилию так и по перемещению.
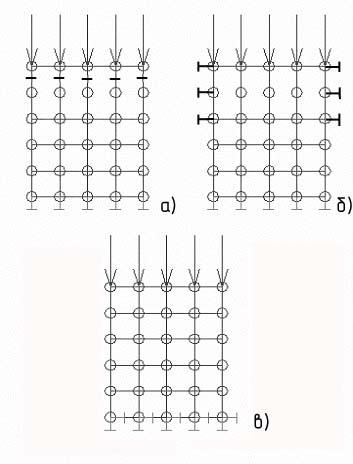
Рисунок 26 – Приложение граничных условий по усилию: а – неверное,
б – используемое для описания перемещения участка модели по направляющим, в – используемый для описания заделки
Следует заметить то, что граничные условия прикладываются к узлам дискретной модели и наибольшее число граничных условий, которое можно применить к каждому узлу это либо 3 силы, либо 3 перемещения. Число граничных условий должно быть обоснованно и минимально необходимо /14/.
Задание ограничений в современных программах очень упрощенно, например, для задания плоскостей симметрии при осадке достаточно указать поверхность симметрии на теле модели, а система сама распознает и накладывает ограничения на те узлы, которые принадлежат к этой плоскости. В случае использования программы граничные условия могут быть приложены к узлу, линии, поверхности или объему, но следует помнить, что с линии, поверхности и объема граничные условия будут перераспределенными на узлы.
2.7 Решение контактных задач.
Особенностью задач ОМД являются наличие больших контактных поверхностей. Так для исследования прочностных характеристик ротора двигателя, необходимо определить контакт на небольшой поверхности в подшипнике, в то время как в случае процесса осадки контактной поверхностью является поверхность двух торцов заготовки.
Следует заметить, что контактные задачи являются достаточно сложными задачами. Общая последовательность решения таких задач сводится к дополнительному заданию условий, действующих на контактных поверхностях. Очевидно, что для задания этих условий необходимо определить контактную пару.
Отличительной особенностью задач ОМД является то, что в ходе технологического процесса контактная поверхность между инструментом и заготовкой претерпевает значительные изменения. Например, в процессе вытяжки (рис. 27) сначала заготовка, матрица и прижим касаются в зоне 1, 2. Контакта между пуансоном и заготовкой нет, затем в зоне 3 происходит касание пуансона и заготовки, при этом матрица и пуансон не контактируют. На следующем этапе возникает контакт в зоне 4 и 5 между матрицей, пуансоном и заготовкой. На заключительном этапе контакт в зоне 1 исчезает.
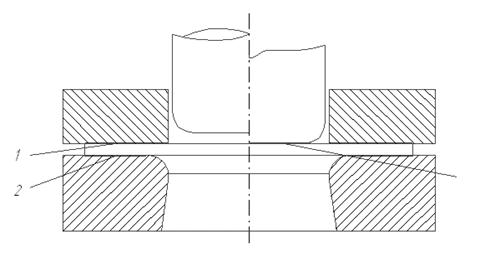
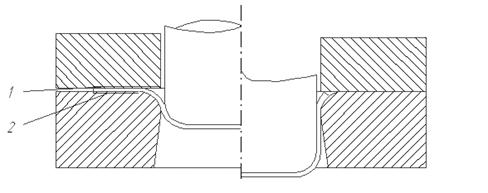
Рисунок 27 – Развитие зоны контакта на различных этапах вытяжки: 1, 2, 3, 4, 5 – зоны контакта, 6 – пуансон, 7 – прижим, 8 – матрица
Из приведенного примера понятно, что математически описать развитие зоны контакта достаточно сложно. Несмотря на это средства, используемые для расчёта контактных задач, должны обеспечить решение с учётом рассмотренной последовательности.
2.8 Задание свойств материала.
Для решения задач механики твердого тела (например, для того чтобы определить какую форму примет тело при штамповке) необходимо знать связь между деформациями и напряжениями, описывающую особенность поведения материала, нагружаемого внешними усилиями. При этом надо учесть тот факт, что свойства различных материалов, используемых для моделирования процессов металлургии, сильно отличаются друг от друга.
Например, хрупкие материалы разрушаются практически сразу после начала пластических деформаций. Пластичные металлы могут значительно деформироваться с момента нагружения до момента разрушения.
Задачи ОМД являются сложными динамическими задачами, отражающими протекание процесса во времени, поэтому для их моделирования вводится дополнительное допущение, связанное с тем, что сложная динамическая задача заменяется по шагам на серию более простых квазистатических задач. Каждая такая задача не рассматривает протекание процесса во времени, а осуществляет статический анализ для одного шага, при этом на каждом последующем шаге используются результаты расчета с предыдущего шага.
Поэтому для описания зависимости между напряжениями и деформацией пользуются несколькими моделями, которые можно разделить на две группы: модели, описывающие упругое и пластичное состояние тела /13/.
2.8.1 Модели, описывающие упругое поведение материала
Наиболее широко используется модель линейного деформирования (закон Гука). Данная модель, как правило, используется при решении конструкционных прочностных задач. На рисунке 28 показано стрелками, что после снятия нагружения деформация в теле равна нулю.
Другой моделью, описывающей поведение нелинейно-упругого материала является мультилинейная упругая модель (рис. 28б). Данная модель в первом приближении заменяет нелинейную упругую зависимость реальных тел с помощью определенного количества отрезков прямых. Такая модель описывает материалы у которых участок линейного упругого деформирования на диаграмме растяжения очень мал, поэтому практически любая нагрузка, выводит тело за приделы линейного упругого деформирования.
 а)
а)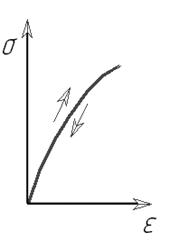 б)
б)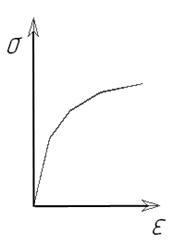 в)
в)
Рисунок 28 – Упругие модели среды:
а- линейная; б – нелинейная; в – мультилинейная упругая
Подобная модель может использоваться для описания свойств объектов, участвующих в процессе деформирования заготовки. Например, может описывать свойства эластичной среды при штамповке.
2.8.2 Модели, описывающие пластическое состояние материала
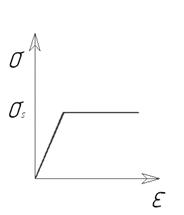
Модели, описывающие пластическое состояние тела, являются наиболее сложными и наиболее часто применяемыми для решения задач ОМД, поскольку эти модели описывают поведение материалов заготовки в ходе деформирования. Среди моделей, описывающих пластическое состояние тела, в теории ОМД обычно выделяют следующие (рис. 29) /13/:
Упруго-пластическая неупрочняемая модель (рис.29а) – материал на начальной стадии деформируется по закону Гука, и по достижению значения придела текучести начинается пластическая деформация материала. Упрочнение не учитывается.
Жесткопластическая модель (рис. 29б) – материал начинает деформироваться по достижению значения напряжения текучести без упругого деформирования на начальном этапе. Упрочнение не учитывается. Напряжение не зависит от деформаций.
 а)
а) 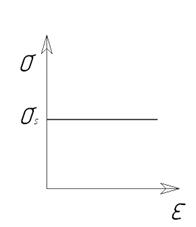 б)
б)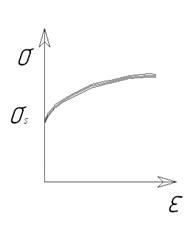 в)
в)
Рисунок 29 – Модели, описывающие пластические свойства материалов:
а – упруго-пластическая неупрочняемая; б – жесткопластическая, несжимаемая, неупрочняемая; в – несжимаемая, упрочняемая, жесткопластичекая
Данные модели, используемые для описания технологических процессов горячей обработки металлов, когда упрочнением в материале можно пренебречь.
Несжимаемая упрочняющаяся модель – упругие деформации отсутствуют, пластическая деформация начинается по достижению напряжениями значения напряжения текучести, которые возрастают в соответствии с условиями упрочнения.
Упругая пластическая упрочняемая модель – как правило, не используется, поскольку интервал упругих деформаций составляет обычно менее 5% от общей деформации заготовки. Поэтому нет смысла использовать более сложную модель.
2.8.3 Модели, используемые при моделировании с помощью ЭВМ
На практике применение моделей, описывающих пластические свойства материалов, описанных выше, усложняет решение задачи, и поэтому обычно при моделировании на ЭВМ применяются простые и достаточно точные билинейные и мультилинейные модели (рис. 30).
Билинейная модель – является апроксиммирующей (заменяющей) кривой растяжения на два отрезка, один из которых описывает упругие свойства модели другой пластические (рисунок 30а). Построение модели для конкретного материала осуществляется за счет задания модуля упругости, модуля пластичности и придела текучести материала. Билинейная модель может учитывать или не учитывать упрочнение материала в ходе процесса.
 а)
а) б)
б)
Рисунок 30 – Наиболее часто употребляемые модели для описания механических свойств материала: а – билинейная модель; б – мультилинейная.
Мультилинейная модель – отличается от билинейной тем, что разбиение диаграммы растяжения осуществляется не на два, а на большее количество отрезков, что позволяет более точно описать поведение реального материала при деформировании. При этом упругий участок по-прежнему описывается одним отрезком (рис. 30б).
Обычно для построения модели свойств материала в программах моделирования есть режим задания свойств материалов виде таблицы (рис. 31). Это зачастую наиболее простой режим задания свойств материала, основанный на легко доступных экспериментальных данных, в ходе которого осуществляется построение графика модели по точкам. При этом построение зависимости осуществляется для заданной температуры. (Например, при холодной листовой штамповке при температере 20˚). В случае если при моделировании процесса надо учитывать влияние температуры на свойства материала (например, как в горячей штамповке), то вводится график еще для нескольких температур, лежащих в интервале изменения температуры тела по ходу процесса.

Рисунок 31 – Таблица задания свойств материала в программе Deform.
При моделировании процессов ОМД иногда приходит сталкиваться с быстро протекающими во времени процессами (штамповка на ВСМ, и т.д.). В этом случае необходимо, чтобы модель учитывала фактор скорости протекания процесса во времени, поскольку при высоких скоростях обработки свойства материалов отличны от свойств материалов при статичной (медленной) обработке.
Следует запомнить, что правильный выбор модели, описывающий свойства объекта позволяет значительно сэкономить время расчета на ЭВМ и получить при этом достоверные результаты.
Например, при расчете процесса штамповки деталей в открытых штампах пренебрегают деформацией инструмента, считая его абсолютно жестким. В этом случае расчет осуществляется быстрее, поскольку компьютеру приходится рассчитывать деформации только одного тела – заготовки, а не трех как в случае если считать что инструмент (верхний и нижний штампы) деформируются упруго.
2.9 Выбор параметров расчета и подготовка к расчету
Для осуществления расчета необходимо помимо граничных условий определить еще дополнительные условия расчета: задание числа шагов, необходимых для расчета, остановки расчета, выбор метода расчета, необходимых для решения конкретной задачи.
Первое что необходимо определить это размер шага для квазистатического анализа. Напомним, понятие квазистатической задачи: для упрощения исследования процессов ОМД исходный, проходящий во времени процесс, рассматривают как набор дискретных статических подзадач, при этом результаты расчёта предыдущей подзадачи являются исходными данными для расчёта последующей подзадачи.
Задание шага задачи можно осуществлять по времени или по перемещению инструмента, при этом перемещение узлов на каждом шаге не должно составлять более 1/3 наименьшего ребра КЭ, участвующего в решении задачи /17, 18/.
Задавая число шагов, фактически задается величина перемещения инструмента в ходе процесса (его положение по окончанию процесса). При необходимости в ряде программ (Например, в программе Deform) можно задать дополнительные условия, позволяющие остановить процесс. В качестве таких условий, как правило, выступают значения перемещения рабочих поверхностей инструмента друг относительно друга.
В зависимости от поставленной задачи осуществляется выбор метода, позволяющего наиболее точно и полно представить результаты решения.
После завершения задания всех условий и исходных данных осуществляется подготовка данных к расчету. Обычно этот этап включает в себя создание базы данных, которая содержит всю необходимую для расчета информацию в виде удобном для быстрой обработки её программой в ходе расчета. Обычно при задании исходных данных используются препроцессорная часть программы, которая работает со своим файлом. Основная задача препроцессорного файла хранить информацию в таком виде, чтобы пользователю удобно было задавать исходные данные, и перемещать данный файл. Файл базы данных имеет другую структуру, поскольку он используется для расчета и работы с постпроцессором.
В ходе подготовки файла базы данных осуществляется и автоматическая проверка исходных данных с указанием возможных ошибок.
На следующем этапе осуществляется расчет задачи. В ходе расчета, как правило, программа моделирования выводит текущую информацию о состоянии и ошибках, возникающих при расчете.
2.10 Анализ полученных результатов
После завершения расчета для извлечения результатов из файла базы данных обычно используют постпроцессор, который позволяет представить полученную информацию в наглядном и удобном для анализа виде.
В качестве исследуемых величин в задачах ОМД, как правило, выступают: деформации, напряжения, усилия, скорости течения и др. При этом информация может быть представлена в векторном или скалярном виде, с помощью графиков, картинок или таблиц. Как правило, при представлении данных в виде картинок используется режим изолиний или полутоновый режим. При этом информация может быть отражена как для текущего шага без учета других шагов, так и с их учетом.
Основным критерием для оценки результатов является здравый смысл, поскольку большая часть ошибок в расчетах связана с невнимательным или неправильным заданием исходных данных.
Можно выделить следующие ошибки, которые наиболее часто встречаются:
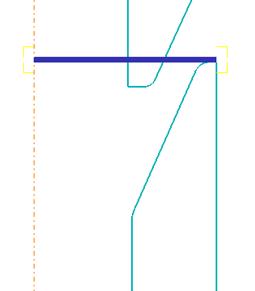
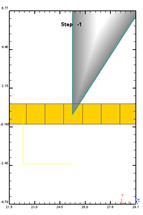
· Инструмент “не видит” заготовку, т.е. проходит сквозь заготовку, не изменяя её форму. Подобная ошибка возникает в двух случаях: в первом – вследствие того, что не были заданы контактные поверхности или поверхности были заданы неверно (рис. 32а), во втором – не задано скругление острых кромок у инструмента (рис. 32б). Во втором случае инструмент “не видит” заготовку, поскольку взаимодействие между ним и заготовкой осуществляется по узлам, а в начальный момент касания инструмента и заготовки таких узлов нет, что позволяет инструменту пройти сквозь заготовку.
 а)
а)
 б)
б)
Рисунок 32 - Неверное назначение поверхности контакта.
После чего положение инструмента уже не может быть интерпретировано программой однозначно и инструмент продолжает проникать сквозь заготовку.
· Образование локальных прострелов (рис. 33) – возникает вследствие неправильного задания шага расчёта больше радиуса КЭ.
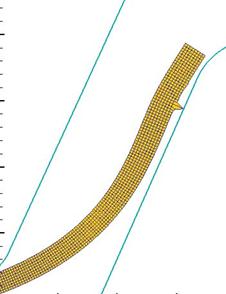
Рисунок 33 - локальный прострел
В этом случае подбор параметров уравнений, описывающих состояние КЭ, осуществляется в соответствии с принципом минимизации энергии, таким образом, что локальный прострел для узлов одного из КЭ более энергетически выгоден, чем перемещение узлов нескольких элементов. Причиной локального прострела узла КЭ сетки является наличие у функционала потенциальной энергии нескольких минимальных значений, т.е. отсутствие унимодальности функционала потенциальной энергии. В этом случае программа находит первое решение, удовлетворяющее условию минимизации энергии и считает его оптимальным.
· Утонение без обрыва в опасном сечении. Подобная ситуация возникает, когда не заданы критерии разрушения материала. В месте локального утонения сетка перестраивается многократно (в случае, если построены подобные установки для автоматического расчёта), но разрушения как у реального тела не происходит (рис. 34).
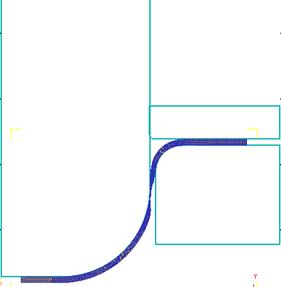

Рисунок 34 – чрезмерное утонение
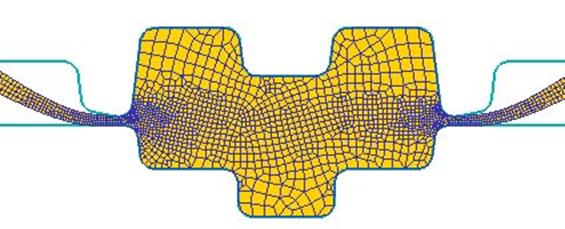
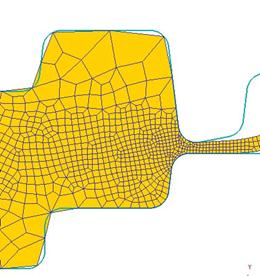
· Укрупнение сетки при малом количестве конечных элементов недостаточном для корректного описания деформируемого тела. Подобная ошибка возникает в том случае, когда программа расчёта может перестраивать сетку в автоматическом режиме. На рисунке 35а показана сетка до автоматического перестроения. В зоне облойной канавки наблюдается интенсивное течение материала, что приводит к значительному искажения сетки. Для избежания больших погрешностей расчёта, связанных с искажением формы КЭ программа автоматически перестраивает сетку КЭ, с параметрами, ориентированными на участок наиболее интенсивного течения металла. Поскольку общее число КЭ недостаточно для корректного описания задачи в полости штампа с менее интенсивным течением металла возникают грубые искажения геометрии заготовки (рис. 35б).
 а)
а)
 б)
б)
Рисунок 35 – Укрупнение сетки при автоматическом перестроении в ходе расчета: а – сетка до перестроения; б – сетка посте перестроения
· Разрывы, возникающие из-за местных дефектов сетки. Данные ошибки расчёта возникают в случае неупорядоченной (свободной сетки). В этом случае возможно возникновение областей значительного искажения сетки, которое может привести к образованию ошибок (вызвать разрушение заготовки).
– Конец работы –
Эта тема принадлежит разделу:
МОДЕЛИРОВАНИЕ ОБЪЕКТОВ В МЕТАЛЛУРГИИ
университет имени академика С П Королева... Ф В Гречников И П Попов А Г Шляпугин...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Последовательность действий, выполняемая при моделировании в CAE-системах, использующих МЭК.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов