рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Теплоотдачи
Реферат Курсовая Конспект
Теплоотдачи
Теплоотдачи - раздел Философия, Тепловые процессы Такой, Как На Рисунке 2.2? Достигнет Ли Вода Точки Кипения В ...
Такой, как на рисунке 2.2? Достигнет ли вода точки кипения в условиях нашей задачи?
Если бы наша банка с водой была идеально изолирована от всего остального пространства, если бы тепло от этого тела не отводилось, то температура повышалась бы пропорционально времени, как на рис. 2.2, и уравнение
(2-1) описывало бы нагрев воды правильно до того момента времени, пока вода не перешла бы в другое агрегатное состояние (закипела).
На самом же деле при мощности кипятильника, например, 300 Вт, вода в ведре не закипит никогда, не закипит она даже в пятилитровой банке. Почему?
Сосуд с водой находится в атмосфере, а воздух – физическое тело. Вода будет иметь все более отличающуюся от воздуха температуру, и по закону природы тепло от более нагретого тела будет естественным путем передаваться к телу менее нагретому - воздуху. Таким образом, воздух будет участвовать в этом процессе в качестве охлаждающей среды.
Для описания процесса передачи тепла от более нагретого тела к телу, менее нагретому, в физике существует такое понятие, как коэффициент теплоотдачи А.Он численно равен энергии, отдаваемой менее нагретому телу (охлаждающей среде) за 1 секунду при повышении разности температур на 1 градус Цельсия.
[А] =Дж/(градсек) =Вт/град.
Итак, тело участвует в двух процессах - нагревается и отдает тепло в охлаждающую среду, причем второй процесс идет тем интенсивнее, чем больше разность температур. Можно предположить, что через какое-то время процесс нагрева тела достигнет такой стадии, когда вся поступаемая от источника тепловая энергия будет передаваться в охлаждающую среду.
В этом случае процесс нагрева тела закончится. Разность
температур больше изменяться не будет ("установится") и будет называться установившейся разностью температур или установившимся перегревом.
Уравнение теплового баланса в этом случае примет вид
Р = А Jу,(2-2)
где Jу - установившаяся разность температур воды и воздуха или установившийся перегрев воды над воздухом.
В дальнейшем буквой J условимсяобозначатьименно перегрев тела над охлаждающей средой.
Рассмотрим следующую ситуацию. Если бы тело имело абсолютную теплоизоляцию, то установившийся перегрев Jубыл бы достигнут за какое-то время Т.На основании уравнения (2-1)энергия, поступившая в тело, полностью пошла на нагрев этого тела
Р Т = C Jу(2-3)
Но с другой стороны из (2-2)
Jу = Р/А(2-4)
Подставляя (2-4) в (2-3) и сокращая Р, получим
Т = C/А = соm /А.(2-5)
Получили какой-то временной показатель, зависящий от характеристик данного тела - материала (сo), массы m, площади поверхности (коэффициент теплоотдачи А), но не зависящий ни от мощности нагрева, ни от температуры. Это соотношение теплоемкости и теплоотдачи называют постоянной времени нагрева тела Т.
Отметим, что эта величина постоянна только для данного тела и для другого нагреваемого тела будет иметь свое значение, отличное от других, причем более массивные тела будут иметь и бо′льшие значения этой постоянной.
Запишем уравнение теплового баланса для элемента
времени dt. Поступившая за этот элемент времени энергия Р dtбудет частично расходоваться на нагревание тела, а частично – передаваться в охлаждающую среду.
Р dt = C dJ + А J dt,(2-6)
где J- разность температуры тела и температуры охлаж-дающей среды, то есть перегрев тела над охлаждающей средой.
Перепишем (2-6) следующим образом
dt(Р - А J) = C dJ.(2-7)
Разделим выражение (2-7) на А
dt(Р/А - J) = С/А dJ(2-8)
и перепишем его с учётом (2-5) и (2-4)
dt (Jу - J) = Т dJ(2-9)
Разделим выражение (2-9) на (Jу - J).
dt = Т dJ/(Jу - J)(2-10)
Интеграл от обеих частей этого уравнения
t = -Т Ln(Jу - J) + В.(2-11)
Постоянную В определим из следующего условия. В начальный момент времени t=0перегрев тела над охлажда-ющей средой имел какое-то начальное значение Jн. Тогда
0 = -Т Ln(Jу - Jн) + В
или
В = Т Ln(Jу - Jн)(2-12)
Подставляя (2-12) в (2-11) получим
dt = -Т Ln(Jу - J) + Т Ln(Jу - Jн).(2-13)
Разделим выражение (2-13) на (-Т).
-t/Т = Ln(Jу - J) - Ln(Jу - Jн)
или
- t/Т = Ln[(Jу - J)/(Jу - Jн)](2-14)
Представим обе части выражения (2-14) в виде
показателей степени основания натуральных логарифмов
Exp(-t/Т ) = (Jу - J)/(Jу - Jн)
или
(Jу - Jн) Exp(-t/Т ) = (Jу - J)(2-15)
Окончательно получим выражение зависимости J=f(t)
J = Jу - (Jу - Jн ) Exp(-t/Т)(2-16)
или
J = Jн Exp(-t/Т) + Jу [1-Exp(-t/Т)](2-17)
Эта форма решения исходного уравнения (2-6) широко применяется при расчетах тепловых процессов на ЭВМ, что будет рассмотрено в следующем параграфе. Для понимания процесса нагревания однородного тела как перехода от начального значения перегрева Jнк устано-вившемуся Jуболее удобна другая форма решения. Прибавим и вычтем из правой части уравнения (2-17) Jн.
J = Jн - Jн + JнExp(-t/Т) + Jу [1-Exp(-t/Т)]
или
J = Jн - Jн[1-Exp(-t/Т)] + Jу[1-Exp(-t/Т)]
или
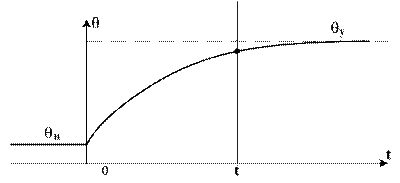
J = Jн + (Jу - Jн)[1-Exp(-t/Т)](2-18)
Здесь первое слагаемое - начальное значение перегрева тела над охлаждающей средой в момент начала действия
нагревающей мощности Р, а второе - температурная разность, которая преодолевается по возрастающей кривой
(рис. 2.3).
Очень важный момент. В исходном дифференциаль-ном уравнении (2-6) было два аргумента – время t и величина нагревающей мощности Р, точнее - аргумент t и параметр Р. Но в полученных выражениях (2-17) и (2-18),
представляющих собой зависимость J=f(t), нагревающая мощностьРотсутствует, выпала из них.
– Конец работы –
Эта тема принадлежит разделу:
Тепловые процессы
Московский государственный университет путей cобщения... МИИТ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Теплоотдачи
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов