рефераты конспекты курсовые дипломные лекции шпоры

Раздел Образование
/
Вид работы: Контрольные Работы
/
Пределы функций, основные теоремы о пределах

Реферат Курсовая Конспект

Выберите учебное заведение

Пределы функций, основные теоремы о пределах

Пределы функций, основные теоремы о пределах - Контрольная Работа, раздел Образование, Методические указания и задания контрольных работ 1. Теоремы О Пределах. Пусть Существуют К...

1. Теоремы о пределах.

Пусть существуют конечные пределы 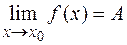и . Тогда справедливы следующие утверждения:

;

;

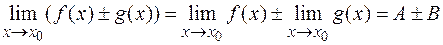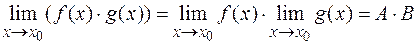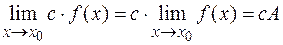, где с – число;

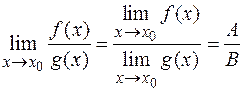, если .

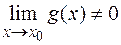2. Бесконечно малые и бесконечно большие функции.

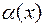Бесконечно малой функцией при называется функция , предел которой равен нулю при : .

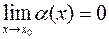Если значения функции f(x) неограниченно возрастают по абсолютной величине при , то такую функцию называют бесконечно большой при . Предел этой функции обозначают знаком бесконечности : .

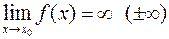Теорема о связи бесконечно малых и бесконечно больших функций.

Если 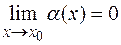, то .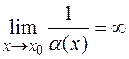

Если 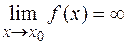, то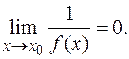

Задача. Вычислить пределы функци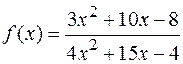и при

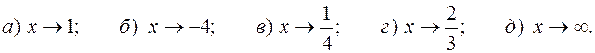
Решение.В задаче следует найти предел частного. С этой целью необходимо вычислить пределы числителя и знаменателя дроби, подставив в них предельное значение аргумента.

а) .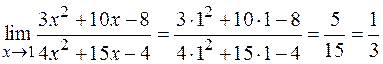

Здесь применима теорема о пределе частного.

б) .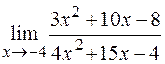

При подстановке 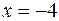в числитель и знаменатель дроби убеждаемся, что их значения равны нулю, поэтому теорема о пределе частного здесь не применима. В данном случае говорят, что имеется неопределенность вида .

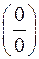Неопределенность вида 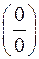при может быть раскрыта сокращением дроби на множитель вида (х–х₀), который обращает числитель и знаменатель дроби в нуль, в данном случае на (х+4). Поэтому, следует разложить на множители числитель и знаменатель дроби (п.2 и п.3 прил.1).

3х²+10х – 8 = 0;	4х²+15х– 4 = 0;
D =	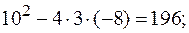D =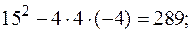

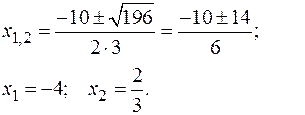
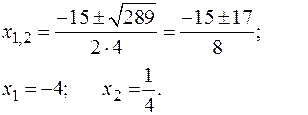
3х²+10х–8 = 3(х+4)(х–2/3) =	4х²+15х – 4 = 4(х+4)(х–1/4 ) =
= (х+4)(3х–2).	= (х+4)(4х–1).

Таким образом,

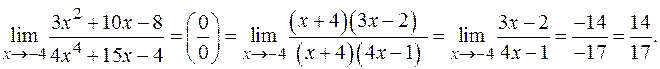
в)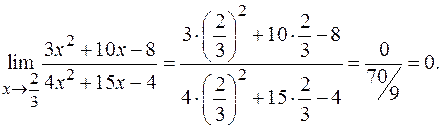

Здесь применима теорема о пределе частного, так как существуют конечные пределы числителя и знаменателя, и предел знаменателя не равен нулю.

г)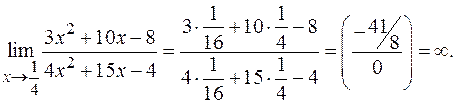

Здесь использована теорема о связи бесконечно малой и бесконечно большой функций.

д) .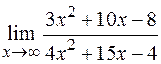

Пределы числителя и знаменателя дроби равны . В этом случае говорят, что имеется неопределенность вида «бесконечность на бесконечность». Теорема о пределе частного здесь не применима.

Чтобы раскрыть неопределенность вида 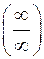при 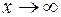, каждый член числителя и знаменателя дроби делят на x в наивысшей степени (в нашем примере на х²), отчего величина дроби не изменится, но исчезнет неопределенность.

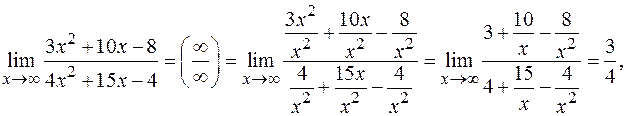
так как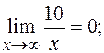

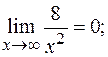
(по теореме о связи бесконечно большой и бесконечно малой функций).

Замечание. Полезно запомнить, что при 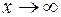предел отношения многочленов c одинаковыми наивысшими степенями равен отношению коэффициентов при этих степенях.

В нашем примере, коэффициенты при наивысшей степени х²многочленов равны 3 и 4, поэтому и предел дроби равен .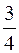

Ответы.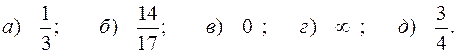

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Методические указания и задания контрольных работ

МАТЕМАТИКА... Методические указания и задания контрольных работ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Пределы функций, основные теоремы о пределах

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ОСНОВНЫЕ ВОПРОСЫ К ЭКЗАМЕНУ ЗА ПЕРВЫЙ КУРС
Тема 1. ЛИНЕЙНАЯ АЛГЕБРА И АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ 1. Определители второго и третьего порядков и их свойства. Миноры и алгебраические дополнения. Разложение определителя по

Тема 3. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ
15. Задачи, приводящие к понятию производной. Определение производной; ее геометрический и механический смысл. 16. Правила дифференцирования функций. Производные основных элементарных функ

Тема 4. ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ
29. Неопределенный интеграл; его свойства. Таблица основных интегралов. 30. Интегрирование заменой переменной; по частям. Интегрирование рациональных дробей. 31. Задачи, приводящи

ПРАВИЛА ОФОРМЛЕНИЯ КОНТРОЛЬНЫХ РАБОТ
При выполнении контрольных работ по математике нужно придерживаться следующих правил: 1. Каждую контрольную работу выполнять в отдельной тетради чернилами любого цвета, кроме красного и зе

Задачи 1–20
Даны вершины треугольника: А(х1; у1), В(х2; у2), С(х3, у3). Сделать чертеж и найти: 1) дли

Задачи 21–30
Решить систему линейных уравнений методом Крамера. 21. 22.

Задачи 31–40
Вычислить пределы функции y=f(x), при указанном поведении аргумента x. 31.

Задачи 41–50
Вычислить пределы, используя замечательные пределы или эквивалентные бесконечно малые функции. 41. а)

Задачи 51– 60
Исследовать на непрерывность функцию y = f (x) и построить ее график. 51.

Задачи 1–10
Найти производные данных функций и их дифференциалы. 1. а)

Задачи 31– 40
Найти неопределенные интегралы. Результаты проверить дифференцированием. 31. а)

Задачи 41–50
Вычислить площадь фигуры, ограниченной заданными линиями. Сделать чертеж. 41.

К ВЫПОЛНЕНИЮ КОНТРОЛЬНОЙ РАБОТЫ 1
В методических указаниях даны образцы решения задач, аналогичных предлагаемым в контрольных работах; обращено внимание на основные трудности и типичные ошибки, которые допускаются с

Аналитическая геометрия на плоскости
1. Основные формулы метода координат. · Формула расстояния между двумя точками А(хA;уA) и В(хB;уB):

Эквивалентные бесконечно малые функции
1. Замечательные пределы: · первый замечательный предел:

Решение.
В рассматриваемых задачах неопределенность вида

Решение.
Очевидно, что Далее воспользуемся вторым з

Непрерывность функции
1.Односторонние пределы функции в точке. · Правый предел:

Производная и дифференциал функции одной переменной
1. Правила дифференцирования. Пусть даны дифференцируемые функции u(x) и

Производная сложной функции.
Сложная функция (суперпозиция функций) – это функция вида y = f(u), где u = u(x) , т.е. функция от функции. Например, · функция

Решение.
а) . Приведем функцию y к виду, удобному для дифференцир

Исследование функции
1.Проиллюстрируем на примере некоторые важные свойства графика функции (рис. 4).

Задача. Исследовать средствами дифференциального исчисления функцию и построить ее график.
Решение. Исследование будем проводить по следующей схеме. 1. Область определения функции. В нашем примере это множество всех действительных чисел,

Неопределенный интеграл, методы интегрирования
1. Понятия первообразной и неопределенного интеграла. Функция

Проверка.

Проверка.
Что и требовалось показать. в.2)

Проверка.
Что и требовалось показать. в.3)

Проверка.
Что и требовалось показать. г.2)

Определенный интеграл, вычисление площадей
1. Понятие определенного интеграла. Определенный интеграл – это число, которое находится по формуле Ньютона-Лейбница:

Справочный материал по элементарной математике
1. Формулы сокращенного умножения:

Графики основных элементарных функций
1. Степенные функции: