Наиболее важные случаи.

1. Сила постоянна.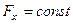

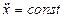
Имеем равнопеременное движение (движение с постоянным ускорением)

2. Сила зависит от времени.

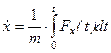
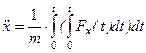
3. Сила зависит от координаты или скорости.

Силу, зависящую от координаты х , создают упругие тела при их деформации (например, сжатая или растянутая пружина).

Сила, зависящая от скорости движения 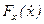, это сила сопротивления (воздуха, воды и т.д.)

В этих случаях решение задачи упрощается.

Лекция 2

Краткое содержание: Свободные колебания без сопротивления. Понятие о фазовой плоскости. Свободные колебания в поле постоянной силы. Параллельное включение упругих элементов. Последовательное включение упругих элементов. Вынужденные колебания без сопротивления. Резонанс. Свободные колебания с вязким сопротивлением. Вынужденные колебания с вязким сопротивлением.

 

Свободные колебания без сопротивления

Существуют устройства (упругие элементы), которые создают силу пропорциональную их удлинению. , Эту силу называют восстанавливающей или центральной силой. Коэффициент пропорциональности называется жесткостью упругого элемента.

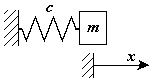
Дифференциальное уравнение движения точки с массой , закрепленной на упругом элементе, имеет вид:

 

Рис. 2-1

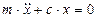или , где

Начальные условия имеют вид: при , .

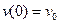Это дифференциальное уравнение свободных колебаний материальной точки без сопротивления.

Характеристическое уравнение имеет вид:

Корни характеристического уравнения равны: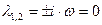

Решение имеет вид:

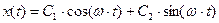
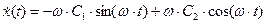
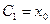
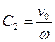
- амплитуда колебаний;

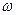- круговая или циклическая частота колебаний (собственная частота). Измеряется в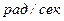

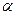- фазовый угол (или просто фаза).

- период колебаний.

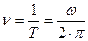- частота колебаний (1 кол./cек=1 Гц)

Рис. 2-2

Движение материальной точки – это свободные гармонические колебания с постоянной амплитудой. Амплитуда колебаний зависит от начальных условий и круговой частоты.

 

Понятие о фазовой плоскости

Обычное описание движения системы с одной степенью свободы в виде зависимости координаты от времени 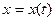не является единственно возможным. В ряде случаев, особенно при изучении нелинейных механических колебаний, определенными достоинствами обладает представление движения на фазовой плоскости.

Состояние системы в любой фиксированный момент времени 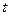определяется парой соответствующих значений и 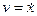и может быть представлено изображающей (фазовой) точкой в плоской декартовой системе координат , , если откладывать по оси абсцисс координату , а по оси ординат –скорость . Такая плоскость называется фазовой.

В процессе движения рассматриваемой системы величины и изменяются и, соответственно, меняется положение изображающей точки на фазовой плоскости. Геометрическое место изображающих точек для данного движения называется фазовой траекторией.

Для построения фазовой траектории при заданном законе движения 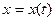нужно путем дифференцирования образовать выражение скорости 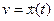, а затем исключить время из двух уравнений: , .

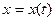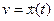Функция и описывает фазовую траекторию данного движения.

Фазовая плоскость особенно удобна для представления колебательных процессов, когда координата и скорость не выходят за известные пределы; поэтому вся картина движения даже в течение неограниченного времени занимает ограниченную часть фазовой плоскости.

Совокупность фазовых траекторий , которая описывает все возможные движения данной системы, называется фазовой диаграммой (фазовым портретом) данной системы.

Для свободных гармонических колебаний 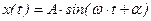, а . Исключая из этих выражений время 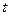получаем

.

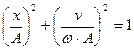Это уравнение эллипса. Его полуоси зависят от амплитуды и круговой частоты.

 

Рис. 2-3

Свободные колебания в поле постоянной силы

На материальную точку кроме упругой силы, действует сила постоянная по величине и направлению.

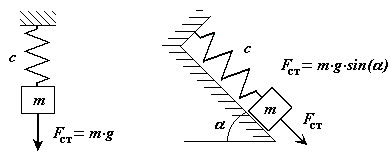
Рис. 2-4

Обозначим ее , тогда дифференциальное уравнение движения точки примет вид:

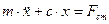или , где

Начальные условия имеют вид: при , .

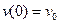Это неоднородное дифференциальное уравнение. Его решение складывается из решения однородного дифференциального уравнения и частного решения неоднородного дифференциального уравнения .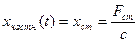

Решение имеет вид:

,

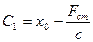
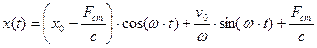Если начало отсчета координаты сдвинуть на , , тогда в новой системе отсчета решение будет иметь вид:

,

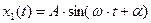
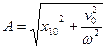- амплитуда колебаний;

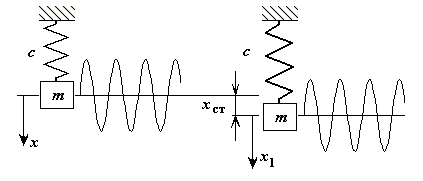
Рис. 2-5

 

Параллельное включение упругих элементов

Масса закреплена с помощью двух упругих элементов расположенных параллельно.

Рис. 2-6

Сместим массу на расстояние . , ,

Результирующая жесткость упругих элементов расположенных параллельно равна сумме жесткостей этих элементов..

 

Последовательное включение упругих элементов

Масса закреплена с помощью двух упругих элементов расположенных последовательно.

 

 

Рис. 2-7

Рис. 2-8

 

 

Сместим массу на расстояние . В упругих элементах возникает восстанавливающая (упругая) сила , одинаковая для обоих элементов. Первый упругий элемент изменит длину на 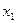, второй - на . . , , .

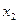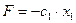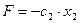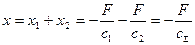, следовательно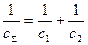

Обратная величина результирующей жесткости упругих элементов расположенных последовательно равна сумме обратных величин жесткостей этих элементов.

Обратная величина жесткости упругого элемента называется податливостью этого элемента.

, , ,

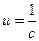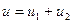
Результирующая податливость упругих элементов расположенных последовательно равна сумме податливостей этих элементов..

 

Вынужденные колебания без сопротивления

Рассмотрим движение точки под действием двух сил: одна восстанавливающая, другая зависит от времени. - гармоническая возмущающая сила.

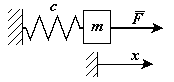
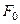- амплитуда возмущающей силы.

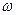- круговая частота возмущающей силы.

 

Рис. 2-9

 

Дифференциальное уравнение движения точки с массой , закрепленной на упругом элементе, под действием возмущающей гармонической силы имеет вид:

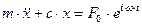
Задавая решение уравнения в виде: 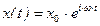и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.

.

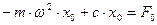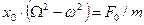Разделим его на массу и обозначим , тогда и окончательно

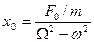- амплитуда вынужденных колебаний.

- частота собственных колебаний

Материальная точка колеблется с амплитудой и частотой возмущающей силы .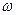

Построим зависимость модуля амплитуды от частоты возмущающей силы .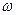

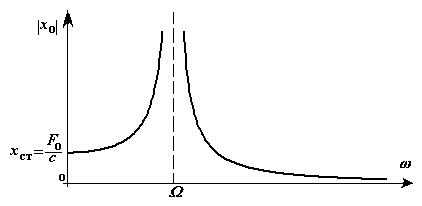
Рис. 2-10

Модуль амплитуды вынужденных колебаний возрастает от 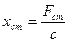(при 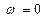) до бесконечности (при 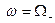) и убывает от бесконечности (при 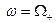) до нуля (при ).

Явление, когда частота возмущающей силы совпадает с собственной частотой колебаний системы, называется резонансом.

 

 

Свободные колебания с вязким сопротивлением

Существуют устройства (демпферы), которые создают силу пропорциональную относительной скорости. 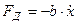. Коэффициент пропорциональности называется коэффициентом демпфирования или коэффициентом вязкого сопротивления.

Дифференциальное уравнение движения точки с массой , закрепленной на упругом элементе и демпфере имеет вид:

 

 

Рис. 2-11

или , , .

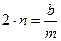Начальные условия имеют вид: , .

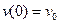Характеристическое уравнение имеет вид: .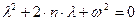

Корни характеристического уравнения равны:

Рассмотрим возможные решения:

1-й случай ,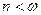

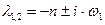
Решение имеет вид:

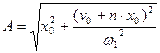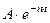, - условная амплитуда затухающих колебаний;

 

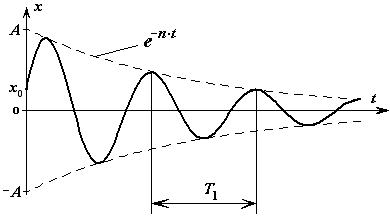
Рис. 2-12

 

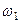- круговая или циклическая частота затухающих колебаний Измеряется в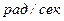

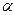- фазовый угол (или просто фаза).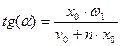

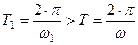- период затухающих колебаний.

- частота колебаний (1 колеб/cек=1 Гц)

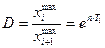- декремент колебаний.

- логарифмический декремент колебаний.

Материальная точка совершает гармонические колебания с частотой 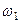и амплитудой, величина которой все время убывает.

Движение изображающей точки на фазовой плоскости показано на Рис. 2-13 .

 

Рис. 2-13

 

2-й случай ,

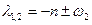
Решение имеет вид:

Материальная точка совершает затухающее неколебательное движение. Рис. 2-14.

Рис. 2-14

3-й случай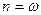, 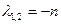(два одинаковых корня)

Решение имеет вид:

Материальная точка так же совершает затухающее неколебательное движение. Рис. 2-14.

 

Вынужденные колебания с вязким сопротивлением

Рассмотрим движение точки под действием трех сил: одна восстанавливающая сила, вторая - сила демпфирования (сила вязкого сопротивления), а третья зависит от времени. - гармоническая возмущающая сила.

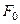- амплитуда возмущающей силы.

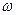- круговая частота возмущающей силы.

Дифференциальное уравнение движения точки с массой , закрепленной на упругом элементе и демпфере, под действием возмущающей гармонической силы имеет вид:

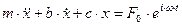
Рис. 2-15

Задавая решение уравнения в виде: 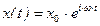и подставляя его в дифференциальное уравнение получим алгебраическое уравнение для определения амплитуды вынужденных колебаний.

.

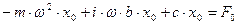Разделим его на массу и обозначим , , 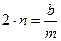тогда и окончательно

- амплитуда вынужденных колебаний.

- частота собственных колебаний

Материальная точка колеблется с амплитудой и частотой возмущающей силы .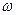

Построим зависимость модуля амплитуды от частоты возмущающей силы .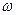

Рис. 2-16

Модуль амплитуды вынужденных колебаний возрастает от 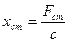(при 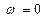) до некоторой величины, а затем убывает до нуля (при ).

Лекция 3

Краткое содержание: Общие теоремы динамики точки. Количество движения точки. Элементарный и полный импульс силы. Теорема об изменении количества движения точки. Момент количества движения точки. Теорема об изменении момента количества движения точки. Работа силы. Мощность. Кинетическая энергия точки. Теорема об изменении кинетической энергии точки. Принцип Даламбера для материальной точки