ПОСТАНОВКА И РЕШЕНИЕ ЗАДАЧ ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Первые упоминания о линейных уравнениях возникли ещё за несколько веков до нашей эры.

В Древней Греции Диофант (II-III в.) формулирует уравнения, в которых искомые переменные – целые. Например, для уравнения первой степени, а₀+а₁х₁=0, где а₀, а₁ – целые, решение х₁ = а₀/а₁ – целое, если а₀ делится на а₁ без остатка, т.е. такое уравнение не всегда разрешимо в целых числах. Из двух уравнений 3х₁–27=0 и 5х₂+21=0 только первое имеет целое решение: х₁=27/3=9, а второе – нет, так как х₂=–21/5.

Для уравнения с двумя неизвестными: а₁х₁+а₂х₂=0, где а₁, а₂ – целые, решение будет х₁=–(а₂/а₁)х₂. Например,

10х₁–5х₂ = 0 или х₁=0,5х₂. (2.2.1)

Из этого примера можно сделать следующие выводы: уравнение имеет бесчисленное множество решений, так как п > т; решение – целое, если х₂ – чётное.

Для того, чтобы из множества допустимых решений выбрать одно – оптимальное, необходимо, как нам уже известно, добавить к условию (2.2.1) целевую функцию. Задачи оптимизации, в которых решение должно быть в целых числах, называют задачами целочисленного программирования. Если в этой задаче целевая функция и ограничения – линейные зависимости, то её называют целочисленной задачей линейного программирования; если же хотя бы одна зависимость будет нелинейной, то такая задача формулируется как целочисленная задача нелинейного программирования.

Большинство практических задач принятия решения сводятся, как правило, к целочисленным задачам линейного программирования.

Если к условию (2.2.1) добавить такие, например, граничные условия:

2 £ х₁ £8; 1£ х₂ £ 3,

то можно видеть, что такая система решения не имеет. Отсюда следует, что задача целочисленного программирования не всегда имеет решения, т.е. она не совместна.

Под целочисленным или дискретным программированием понимают такие задачи (обычно линейные), в которых искомые переменные по смыслу могут принимать только целые значения: число рабочих, разделяемых по рабочим местам, количество единиц оборудования, устанавливаемых на заданной площади и т.п.

Аналитическая задача целочисленного программирования формулируется:

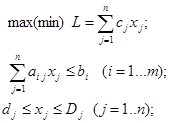
где х_j = 0,1,2,... целые (j = 1...n₁ £ n).

Если п₁ = п, то задачу называют полностью целочисленной, если п₁ < п, то – частично-целочисленной.

Предположим, что задача имеет многогранник решений (рис.2.2.1). Если наложить требование целочисленности, то допустимое множество решений выразится в системе точек и уже не является выпуклым.

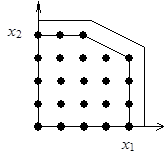
Рис.2.2.1

Если добавить новые ограничения, связывающие внешние целочисленные точки, а затем в качестве многогранника использовать всё выпуклое множество, ограниченное осями координат и новым контуром, то получим новую задачу линейного программирования со следующими свойствами:

- новый многогранник решений содержит все целые точки, заключавшиеся в первоначальном многограннике решений; любая его угловая точка целая;

- так как целевая функция достигает оптимума в угловой точке, то построением многогранника обеспечивается целочисленность оптимального решения.

Таким образом, решение задач целочисленного программирования – трудоёмко. Поэтому по возможности лучше не накладывать ограничений целочисленности переменных.

В ряде случаев целочисленного программирования решают следующим образом.

1. Как непрерывную задачу линейного программирования.

2. Округляют переменные.

3. Проверяют допустимость округлённого решения.

4. Если решение допустимое, то оно принимается как целочисленное.

При необходимости точного решения применяют специальные методы, где учитывается, что множество решений любой целочисленной задачи – конечно. Например, в задаче с переменными х₁, х₂: 0< x₁ £ 4; 0< x_j£ 5. Число возможных решений 4*5=20. Следовательно, возможен полный перебор всех возможных сочетаний целочисленных х₁, х₂ и выбор из них наилучших в смысле целевой функции. Трудоёмкость этого метода возрастает с ростом числа переменных и области граничных условий, и для реальных задач неприменим.

Поэтому в реальных задачах применяют методы, в которых не рассматривают все возможные альтернативы. Распространены методы отсечений и методы возврата, среди которых наиболее известен метод ветвей и границ. Метод отсечений для программной реализации сложен.

Метод ветвей и границ. Задача линейного программирования решается без учёта целочисленности. Такая задача называется непрерывной. Далее рассматривают одну из переменных x_j, на которую накладывают ограничение целочисленности, но которая получила дробное значение. На основе полученного решения составляют дополнительные ограничения:

x_j £ [x^*_j] и x_j ³[x^*_j]+1,

где [x^*_j] – целая часть нецелочисленного значения переменной x^*_j в оптимальном решении, и затем решаются ещё две задачи линейного программирования, в каждую из которых вошли все исходные ограничения и одно из дополнительных

Полученное решение новых задач проверяют на целочисленность переменных. Если решение не удовлетворяет требованию целочисленности, на основе каждой из задач составляют две новые аналогично предыдущим и т.д.

Если одно из решений удовлетворяет требованию целочисленности, значение целевой функции принимается за граничное L_гр. При этом рассмотрение других задач продолжается до тех пор, пока не будет получено:

- на одной из ветвей недопустимое решение;

- на одной из ветвей целочисленное решение. Тогда значение целевой функции сравнивается с L_гр (верхним – при max, нижним – при min); если полученное значение хуже, оно отбрасывается; если лучше – то принимается за граничное;

- на одной из ветвей целочисленное решение, однако при этом значение целевой функции хуже граничного. Тогда дальнейшее рассмотрение также прекращается.

На первом цикле расчёта

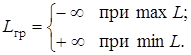
Таким образом, для получения целочисленного решения методом ветвей и границ приходится решать большое число задач линейного программирования, причём в каждом очередном ветвлении число ограничений увеличивается на 1. Поэтому время решения задачи целочисленного программирования по сравнению с непрерывной значительно увеличивается.

Пример.

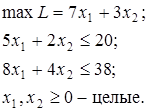
Решение. В результате решения задачи симплекс-методом найдём оптимальное решение: ; L₁ = 29,5; где верхний индекс переменных – номер задачи.

В полученном решении х₂ = 7,5 – нецелочисленное. Поэтому для дальнейшего решения составляем две новые задачи с различными граничными условиями.

Задача 2:

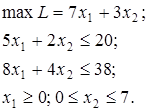
Задача 3:

Результаты решения симплекс-методом задачи 2: 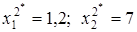; L₂ = 29,4; задачи 3: ; L₃ = 29,25.

В задаче 1 переменная х₁¹=1 – целочисленная, а в последующих задачах при целочисленности х₂, х₁ перестала быть целочисленной. Затем следует накладывать ограничения целочисленности на х₁ и т.д. (рис.2.2.2).

Рис.2.2.2

Результаты решения непрерывной и целочисленной задачи вводятся в табл.2.2.1. В качестве оптимального принимается решение задачи 5, которое даёт наибольшее из целочисленных решений значение целевой функции.

Таблица 2.2.1

№ задачи	х1	х2	L
		7,5	29,5

Из примера видно, что метод ветвей и границ достаточно трудоёмкий. При этом оптимальное решение может быть получено в результате сравнения всех допустимых целочисленных решений.

Поэтому при решении задач реальной размерности может потребоваться память, не имеющаяся даже у современных компьютеров или потребоваться практически неприемлемое время решения.

Обязательное условие метода – наличие верхних границ на значения переменных D_j. Если D_j не назначена, то её определяют по зависимости:

,

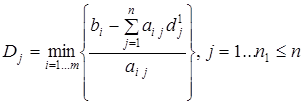где - минимальные значения всех х_j, для которых определяется верхняя граница D_j.