рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- УРАВНЕНИЕ ШРЕДИНГЕРА
Реферат Курсовая Конспект
УРАВНЕНИЕ ШРЕДИНГЕРА
УРАВНЕНИЕ ШРЕДИНГЕРА - раздел Механика, УРАВНЕНИЕ ШРЕДИНГЕРА Рассмотрим Простой Пример Движения Частицы. Пусть Ее Состояние Таково, Что ...
Рассмотрим простой пример движения частицы. Пусть ее состояние таково, что координата частицы имеет определенное значение x. Это значит, что соответствующий вектор |cxñ есть собственный для оператора координаты  :
:
 |cxñ = x|cxñ.
|cxñ = x|cxñ.
Разложим по всем таким состояниям произвольный вектор |yñ:
|yñ = òdx|cxñácx|yñ,
где учтено, что из физических соображений спектр координаты - чисто непрерывный. Таким образом, вектор |yñ задается континуальным множеством чисел
ácx|yñ º y(x),
т.е. фактически некоторой функцией y(x) от x. Она называется волновой функцией частицы. Из нормированности вектора |yñ имеем:
1 = áy|yñ = òdxRdxáy|c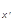 ñác
ñác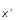 |cxñácx|yñ =
|cxñácx|yñ =
= òdxRdxáy|c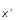 ñ d(x-xR)ácx|yñ = òdxy*(x)y(x)dx = òdx|y(x)|2,
ñ d(x-xR)ácx|yñ = òdxy*(x)y(x)dx = òdx|y(x)|2,
т.е. волновая функция нормируется условием
ò|y(x)|2 dx = 1.
Волновая функция y(x) -это координатная реализация вектора |yñ состояния y из абстрактного гильбертова пространства квадратично интегрируемой функцией, т.е. вектором из функционального пространства L2. Если векторы |y1ñ и |y2ñ нормируемы, то их скалярное произведение теперь запишется как функциональное скалярное произведение:
áy1|y2ñ = òdxy*1 (x)y2 (x)
(доказательство такое же, как при получении условия нормировки).
Возьмем произвольный вектор |yñ, подействуем на него оператором  и введем обозначение
и введем обозначение
 |yñ º |
|yñ º | ñ.
ñ.
Для волновой функции состояния  имеем:
имеем:
 (x) = ácx |
(x) = ácx | ñ = ácx|
ñ = ácx| |yñ º (cx,
|yñ º (cx, y) = (
y) = ( cx,y) =
cx,y) =
= x (cx,y) = xyx.
Таким образом,
 y(x) = xy(x) Û
y(x) = xy(x) Û  = x,
= x,
т.е. в координатной реализации оператор  есть просто оператор умножения на независимую переменную x. Для среднего значения координаты в состоянии y имеем:
есть просто оператор умножения на независимую переменную x. Для среднего значения координаты в состоянии y имеем:
áxñy = áy | |yñ º áy1|y2ñ = òy*1 (x)y2 (x)dx =
|yñ º áy1|y2ñ = òy*1 (x)y2 (x)dx =
= òy* (x){xy(x)}dx,
т.е.
áxñy = òdx×x|y(x)|2.
Это выявляет физический смысл волновой функции - квадрат ее модуля |y(x)|2 задает плотность вероятности обнаружить частицу в точке с координатой x. Результат ясен и из общей теории - из определения y(x) как ácx|yñ и из вероятностной интерпретации ácx|yñ (см. РЕЗЮМЕ). Можно сказать также, что y(x) = ácx|yñ есть амплитуда вероятности перехода частицы из состояния y в состояние cx (см. постулат II).
Вообще говоря, волновая функция зависит не только от координаты, но и от времени. В фиксированный момент времени t0 функция y(x,t0) однозначно определяет состояние y. Очевидно из принципа причинности, что она должна определять и дальнейшую эволюцию системы, т.е. состояние y в произвольный момент времени t, т.е. волновую функцию y(x,t). Поэтому волновая функция должна подчиняться некоторому дифференциальному уравнению первого порядка по времени, для однозначного отыскания решения которого как раз и достаточно задать y(x,t0), (но не ее производные). Поэтому можно записать
 .
.
Здесь множитель i выделен для удобства (чтобы было 
 =
=  - см. ниже), а
- см. ниже), а  - некоторый дифференциальный оператор, не включающий производных по времени. Он должен быть линейным, чтобы соблюсти принцип суперпозиции.
- некоторый дифференциальный оператор, не включающий производных по времени. Он должен быть линейным, чтобы соблюсти принцип суперпозиции.
Докажем эрмитовость оператора  . Имеем очевидное равенство
. Имеем очевидное равенство
 ,
,
так как дифференцируется полная вероятность, т.е. 1. Вносим производную под знак интеграла и дифференцируем:
 .
.
Подставляем производные 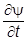 и
и  из уравнения и сопряженного ему:
из уравнения и сопряженного ему:
 ,
, 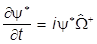 .
.
Получаем
0 = ò dx (y* +y - y*
+y - y* y),
y),
т.е.
 y*
y* ydx = ò
ydx = ò +ydx Û (y,
+ydx Û (y, y) = (y,
y) = (y, y).
y).
В силу произвольности y это и означает эрмитовость  :
:
 =
=  +.
+.
Рассмотрим систему, на которую не действуют нестационарные внешние силы. Это значит, что оператор  не зависит от времени, и решение уравнения можно искать методом разделения переменных. Ищем частное решение в виде
не зависит от времени, и решение уравнения можно искать методом разделения переменных. Ищем частное решение в виде
y(x,t) = Q(t)y(x)
и подставляем в уравнение
 ,
,
где w - константа разделения переменных, не зависящая от x и t. Для Q(t) сразу получаем решение
Q (t) = const.e-iwt.
Значения же w находятся как собственные значения оператора  :
:
 y(x) = wy(x).
y(x) = wy(x).
Их может быть много, а значит, будет много и частных решений с разными w. Считая их спектр дискретным, запишем общее решение как
y(x,t) = 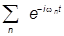 yn (x)
yn (x)
(коэффициенты линейной комбинации включаем в yn (x)).
Разложим функции yn (x) в интеграл Фурье и подставим в y(x,t):
y(x,t) = 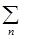 òdk
òdk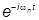 +ikx
+ikx (k).
(k).
Вводя обозначения
E º iw, p º ik,
получим:
y(x,t) =  òdp
òdp
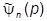 ,
,
где

 .
.
Смысл E-энергия, p - импульс (см. волны де Бройля в лекции 1).
Теперь мы хотим извлечь отсюда явный вид операторов энергии и импульса. Для этого сделаем отступление. Пусть  - произвольный оператор, и |jnñ - его собственные функции. Разложим по ним произвольный вектор |yñ:
- произвольный оператор, и |jnñ - его собственные функции. Разложим по ним произвольный вектор |yñ:
|yñ =  cn|jnñ
cn|jnñ
и подействуем на него оператором :
:
 |yñ =
|yñ =  cnAn|jnñ .
cnAn|jnñ .
Характерный признак действия оператора на разложение: он «вышибает» из каждого слагаемого соответствующее свое собственное значение. Берем теперь найденное разложение для y(x,t) и действуем на него оператором
и действуем на него оператором 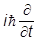 :
:
 y(x,t) =
y(x,t) =  òdpEn
òdpEn 
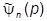
Так как «вышиблись» значения энергии En, то оператор энергии есть
 =
=  .
.
Аналогично,
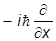 y(x,t) =
y(x,t) =  òdp×p
òdp×p
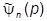 ,
,
а потому оператором импульса является
 =
= 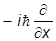 .
.
Возьмем теперь наше исходное уравнение и умножим его обе части на i:
 = i
= i y(x,t).
y(x,t).
Слева стоит оператор энергии, а значит справа - оператор Гамильтона
i =
=  .
.
В итоге приходим к основному динамическому уравнению квантовой механики - к уравнению Шредингера
 =
=  y(x,t).
y(x,t).
Мы рассмотрели одномерный случай. В трехмерном случае y = y(r,t), где r=(x, y, z). Общее решение уравнения Шредингера запишется как
y(r,t) =  òdp
òdp
 .
.
Операторы
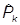 =
= 
есть операторы k-х компонентов импульса. Сам же оператор вектора импульса будет таким:
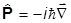 .
.
Чтобы записать в явном виде уравнение Шредингера, надо знать явный вид оператора Гамильтона  . Он строится по принципу соответствия. Один из его аспектов гласит:
. Он строится по принципу соответствия. Один из его аспектов гласит:
– Конец работы –
Эта тема принадлежит разделу:
УРАВНЕНИЕ ШРЕДИНГЕРА
ВОЛНОВАЯ ФУНКЦИЯ ЧАСТИЦЫ УРАВНЕНИЕ... Если в классической механике некоторая динамическая величина есть функция каких то других динамических величин то при...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: УРАВНЕНИЕ ШРЕДИНГЕРА
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов