рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Закон сохранения механической энергии
Реферат Курсовая Конспект
Закон сохранения механической энергии
Закон сохранения механической энергии - раздел Механика, Закон сохранения импульса I. Для Системы Частиц (Или Системы Твёрдых Тел) Второй Закон Ньютона Можно За...
I. Для системы частиц (или системы твёрдых тел) второй закон Ньютона можно записать в виде (§7, ур-e (7.1))
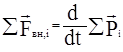 , (15.1)
, (15.1)
где 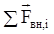 - сумма внешних сил, действующих на тело;
- сумма внешних сил, действующих на тело;  - импульс системы;
- импульс системы; 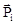 - импульс i-ого тела.
- импульс i-ого тела.
Если внешние силы, действующие на систему, равны нулю, то система называется замкнутой. Для такой системы
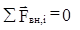 (15.2)
(15.2)
Из (15.2) и (15.1) получим для замкнутой системы
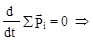
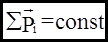 (15.3)
(15.3)
Т.е. сумма импульсов тел в замкнутой системе не меняется. Это есть закон сохранения импульса.
Очевидно, что если внешние силы не равны нулю, но их сумма равна нулю (ур-ние (15.2)), то и в этом случае выполняется соотношение (15.3). Таким образом, в замкнутой системе, а также в системе, в которой 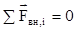 , выполняется закон сохранения импульса.
, выполняется закон сохранения импульса.
Из сказанного выше можно сделать два вывода:
1. Т.к. в замкнутой системе 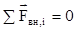 , то в такой системе скорость тел (импульс) меняется только вследствие действия внутренних сил. Практически большинство систем не замкнуты, но если в системе скорости тел меняются в основном вследствие действия внутренних сил, то такую систему с достаточной степенью точности можно считать замкнутой.
, то в такой системе скорость тел (импульс) меняется только вследствие действия внутренних сил. Практически большинство систем не замкнуты, но если в системе скорости тел меняются в основном вследствие действия внутренних сил, то такую систему с достаточной степенью точности можно считать замкнутой.
2. В §7 показано, что
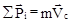 ,
,
где m - суммарная масса тел системы; 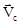 - скорость центра инерции.
- скорость центра инерции.
Из (15.3) и последнего уравнения получим, что в замкнутой системе

Т.е. в замкнутой системе скорость центра инерции системы постоянна.
Запишем проекцию уравнения (15.1) на некоторую ось”Z”:

Если åFвн,Z=0 , то (аналогично (15.3)) получим:
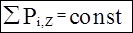 (15.3a)
(15.3a)
В этом случае не меняется сумма проекций импульсов тел на ту ось, для которой сумма проекций внешних сил равна нулю.
II. Правило моментов для системы тел, вращающихся вокруг оси, не меняющей своего направления в пространстве, имеет вид
(§9, ур-е (9.6)):
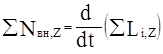 , (15.4)
, (15.4)
где åNвн,Z - суммарный момент внешних сил относительно оси вращения, åLi,Z - суммарный момент импульсов тел относительно оси вращения.
Если
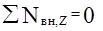 , (15.5)
, (15.5)
то из (15.4) , аналогично (15.3), получим:
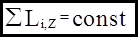 (15.6)
(15.6)
Таким образом, если выполняется (15.5), то выполняется закон сохранения момента импульса относительно оси вращения.
( Ур-ние (15.6) - частный случай векторного закона сохранения момента импульса в замкнутой системе. Ур-е (15.6) аналогично ур-нию (15.3а), но записанно для вращательного движения относительно оси “Z”.)
III. Работа неконсервативных сил равна (§14, ур-е (14.4)):
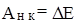 (15.7)
(15.7)
Если на систему действуют только консервативные силы, то
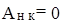 (15.8)
(15.8)
Из (15.7) и (15.8) следует:
 Þ
Þ
 Þ
Þ 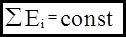 (15.9)
(15.9)
Таким образом, в системе, в которой действуют только консервативные силы (т.е. нет неконсервативных сил или их работа равна нулю) выполняется закон сохранения механической энергии.
Закон сохранения механической энергии - это частный случай общего закона сохранения энергии, который гласит: энергия не возникает и не исчезает, а переходит из одного вида в другой.
Рассмотренные законы сохранения являются следствием свойств пространства. Законы сохранения - одни из фундаментальных законов природы.
Пример. Удар тел.
Выполняется закон сохранения импульса, т.к. в этом случае скорость тел меняется в основном вследствие действия внутренних сил.
|
а) Неупругий удар - скорость тел после удара одинаковая (рис. 15.1); механическая энергия после удара уменьшается т.к. часть её идет на деформацию тел - т.е. не выполняется закон сохранения механической энергии.
|
б) Упругий удар - скорость тел после удара разная (рис. 15.2); выполняется закон сохранения механической энергии. Если положения центров тяжести тел после удара не меняются, то остается постоянной и потенциальная энергия. Следовательно, в этом случае, закон сохранения механической энергии означает, что кинетической энергии тел до и после удара не меняется.
§ 16. Условие равновесия механической системы. Потенциальная яма, потенциальный барьер
|
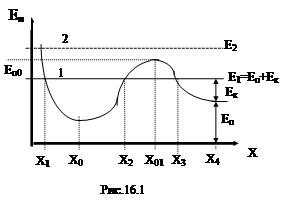
Рассмотрим одномерное движение частицы, у которой зависимость потенциальной энергии от ее положения E(x) имеет вид, показанный на рис 16.1. На частицу действует консервативная сила, проекция которой на ось X, согласно (13.4), равна:
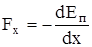 (16.1)
(16.1)
Будем считать, что другие силы на частицу не действуют, т.е. выполняется закон сохранения механической энергии (§ 15):
E = Eп + Eк = const (16.2)
Если на графике потенциальной энергии отложить значения Е, то получим прямую линию, параллельную оси Х (на рис 16.1 - линии 1 и 2, соответствующие двум разным значениям Е). По графикам Е и ЕП можно определить как величину ЕП так и ЕК (на рис 16.1 эти величине указаны для полной энергии Е1 в точке Х4). Из ур-я (16.2) и рисунка видно , что при механической энергии, равной Е1, для точек
Х < Х1 ; Х2 < Х < Х3
ЕК < 0. Отрицательное значение кинетической энергии не имеет физического смысла, а значит, в этих точках частица быть не может.
В точках экстремума (т.е. в точках Х0 и Х01) производная равна нулю:

Учитывая (16.1) получим, что в точках Х0 и Х01 сила, действующая на частицу, равна нулю. Если частица находится в этих точках и скорость её равна нулю, то она в них может находиться сколь угодно долго - эти точки соответствуют положению равновесия частицы. В точке Х0 - положение устойчивого равновесия; в точке Х01 - положение неустойчивого равновесия. Таким образом, минимум потенциальной энергии соответствует положению устойчивого равновесия; в этом положении сила, действующая на тело, равна нулю.
Рассмотрим частицу, которая находится в точке с координатой Х1. В этом положении ее кинетическая энергия равна нулю (т.к. здесь Е1 = Еп => ЕК = 0), следовательно равна нулю и скорость. Однако в этом положении на частицу действует сила, для которой, согласно графика и ур-я (16.1), Fx > 0. Под действием силы частица начнет двигаться в положительном направлении оси Х, её потенциальная энергия будет уменьшаться, а кинетическая энергия расти (ур-е (16.2)). В точке Х0 потенциальная энергия достигнет своего минимального значения, а кинетическая, соответственно - максимального. Т.к. в точке Х0 у частицы есть скорость она продолжит движение. При этом её потенциальная энергия будет расти, а кинетическая энергия - уменьшаться. В точке с координатой Х2 частица остановится т.к. в этой точке (также как и в точке Х1) её кинетическая энергия равна нулю. Далее движение повториться в обратном порядке от точки Х2 до точки Х1 и т.д.
Область между точками Х1 и Х2 называется потенциальной ямой. Из сказанного выше следует, что частица в потенциальной яме совершает колебательное движение.
Область между точками Х2 и Х3 для частицы с механической энергией Е1 не достижима. Эту область пространства называется потенциальным барьером (на рис 16.1 ЕП0 - высота потенциального барьера). Для того чтобы частица смогла преодолеть потенциальный барьер ее механическая энергия должна быть больше высоты потенциального барьера, например, такая как Е2 на рис. 16.1.
– Конец работы –
Эта тема принадлежит разделу:
Закон сохранения импульса
Закон сохранения импульса... Закон сохранения момента импульса Закон сохранения механической...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Закон сохранения механической энергии
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?








Новости и инфо для студентов