рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Решение дифференциального уравнения гармонических колебания.
Реферат Курсовая Конспект
Решение дифференциального уравнения гармонических колебания.
Решение дифференциального уравнения гармонических колебания. - раздел Механика, Механические гармонические колебания Если Взять Уравнение: ...
Если взять уравнение:
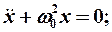
Его решение:
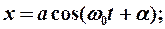
где  и
и 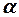 - постоянные;
- постоянные;
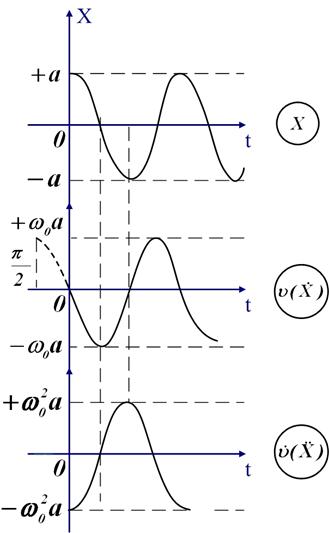
Итак, смещение X изменяется по закону косинуса. Это гармонические колебания:

 - фаза колебаний;
- фаза колебаний;
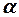 - начальная фаза;
- начальная фаза;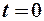 ;
;
 - период;
- период;  - амплитуда;
- амплитуда;
За фаза изменяется на
фаза изменяется на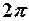 ;
;
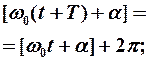
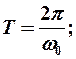
Частота:
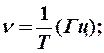
Циклическая частота, число колебаний за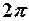 секунд:
секунд:
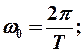

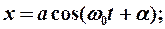
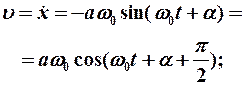
Скорость изменяется также по гармоническому закону, амплитуда скорости =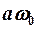 , и она опережает смещение по фазе
, и она опережает смещение по фазе  .
.

Ускорение и смещение в противофазе:
В процессе колебаний происходит превращение кинетической энергии в потенциальную и обратно:


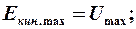

Полная энергия в любой момент времени – постоянная;
– Конец работы –
Эта тема принадлежит разделу:
Механические гармонические колебания
Механические гармонические колебания... Общие сведения о колебаниях...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Решение дифференциального уравнения гармонических колебания.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов