РЕЛЯТИВИСТСКИЙ ИМПУЛЬС. СОХРАНЕНИЕ РЕЛЯТИВИСТСКОГО ИМПУЛЬСА. РЕЛЯТИВИСТСКАЯ ЭНЕРГИЯ

Уравнения Ньютона инвариантны по отношению к преобразованиям Галилея. Однако к преобразованиям Лоренца они оказываются неинвариантными. В частности, не инвариантен к преобразованиям Лоренца вытекающий из законов Ньютона закон сохранения импульса.

В теории относительности импульс, как и в Ньютоновской механике, равен произведению массы тела на его скорость

(6.5)

Однако в выражении (6.5) масса не является постоянной величиной, а зависит от скорости по закону

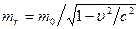. (6.6)

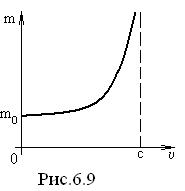
Величина называется массой покоя, это инвариантная величина, масса носит название релятивистской массы. Зависимость релятивистской массы от скорости представлена на рис.6.9.

Продифференцировав выражение (6.5) по времени, получаем релятивистское выражение второго закона Ньютона

Чтобы найти релятивистское выражение для энергии, умножим это уравнение на перемещение частицы :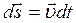

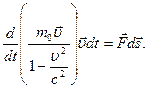
Правая часть этого выражения равна работе, совершаемой над частицей за время dt. Как следует из закона сохранения энергии, эта работа равна приращению энергии частицы:

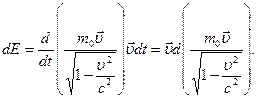
Преобразуем полученное выражение:

Проинтегрировав, имеем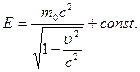

Экспериментально доказано, что константа в этом выражении равна нулю. Тогда полная энергия частицы

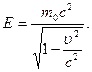(6.7)

Если скорость частицы равна нулю, энергия 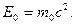Это энергия покоя. Она не связана ни с каким движением частицы. Для произвольного тела энергия покоя равна сумме энергий покоя всех его частиц, кинетических энергий этих частиц в системе центра масс тела и потенциальных энергий взаимодействия этих частиц. В энергию покоя, как и в полную энергию, не входит потенциальная энергия тела в поле внешних сил.

Очевидно, кинетическая энергия равна разности между полной энергией и энергией покоя частицы:

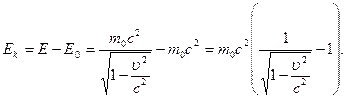
В случае малых скоростей эта формула преобразовывается к виду:

Мы получили классическое выражение для кинетической энергии частицы.

Решив совместно уравнения (6.5), (6.6) и (6.7), получаем:

. (6.8)

При 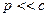имеем: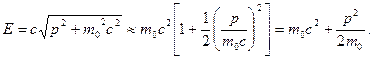

Это выражение отличается от классического выражения для кинетической энергии слагаемым .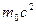

Из выражения (6.7) следует еще одна формула для энергии: 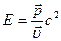. Тогда импульс частицы

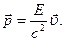
Получим еще одну формулу для энергии. Из замедления времени получаем

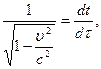
где 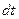- промежуток времени между двумя происходящими с частицей событиями, отсчитанный по часам в той системе отсчета, в которой частица движется, - тот же промежуток времени, отсчитанный по часам, движущимся вместе с частицей. Подставив это выражение в формулу (6.7), имеем

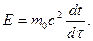(6.9)

Получим теперь преобразования импульса и энергии. Из (6.8) следует

(6.10)

Масса является инвариантом, следовательно, и выражение (6.10) представляет собой инвариант, т.е. имеет одинаковую величину во всех инерциальных системах отсчета. Сами по себе величины E и не являются инвариантами, так как они зависят от скорости, которая меняется при переходе из одной системы отсчета в другую.

Будем считать, что частица движется параллельно оси x, в системе 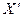скорость частицы равна 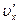. Тогда согласно релятивистской теореме сложения скоростей скорость в системе X равна

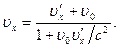(6.11)

Здесь 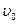- скорость, с которой система 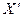движется относительно системы X. Энергию в системе X выразим через 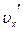. Для этого вычислим выражение :

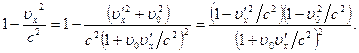
Тогда энергия

 

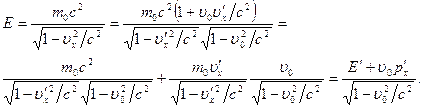
Полученная формула справедлива при любой взаимной ориентации векторов 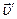и 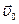. Это означает, что в преобразованиях участвует только компонента импульса 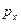. Так как 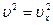, выражение для импульса принимает вид =.

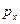Подставим в него 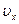из (6.11), имеем

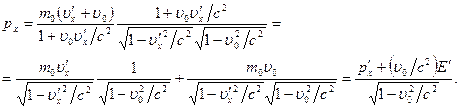
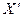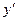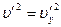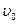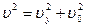
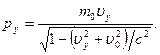Теперь будем считать, что в системе частица движется параллельно оси и, следовательно, . В системе X компонента скорости частицы по оси x равна , так что . Соответственно, Так как 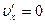, то из преобразований Лоренца для скоростей , и

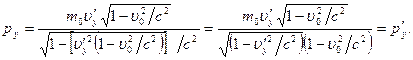
Аналогичный результат получается для компоненты . Тогда преобразования для энергии и импульса принимают вид:

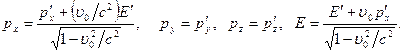
Эти формулы совпадают с формулами (6.2) преобразования координат и времени.

По аналогии с трехмерными векторами в евклидовом пространстве можно определить четырехмерные векторы. Под четырехмерным вектором понимают совокупность четырех величин 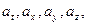преобразующихся по тем же формулам, что и ct, x,y, z. Квадрат такого вектора равен . Вследствие того, что компоненты преобразуются так же, как координаты, квадрат четырехмерного вектора оказывается инвариантным по отношению к преобразованиям Лоренца. Тогда совокупность величин 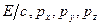образует четырехмерный вектор, называемый вектором энергии-импульса. Квадрат этого вектора является инвариантом и равен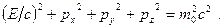

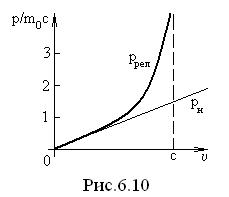
Зависимость релятивистского импульса от скорости представлена на рис.6.10. При малых скоростях релятивистский импульс совпадает с классическим.