Момент импульса частицы. Момент силы. - раздел Механика, Кинематика поступательного движения Кроме Энергии И Импульса Существует Ещё Одна Физическая Величина, С Которой С...
Кроме энергии и импульса существует ещё одна физическая величина, с которой связан закон сохранения — это момент импульса. Моментом импульса частицы 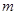 относительно точки О называется вектор
относительно точки О называется вектор 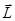 равный векторному произведению
равный векторному произведению 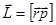 , где
, где 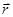 -радиус-вектор частицы,
-радиус-вектор частицы, 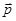 -ее импульс.
-ее импульс.
Момент импульса 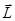 является псевдовектором. Его направление выбрано так, что вращение вокруг точки О в направлении
является псевдовектором. Его направление выбрано так, что вращение вокруг точки О в направлении 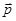 и вектор
и вектор 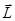 образуют правовинтовую систему. Модуль
образуют правовинтовую систему. Модуль 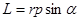 , где
, где 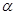 угол между
угол между 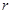 и
и  , а
, а
 плечо вектора
плечо вектора  относительно точки О.
относительно точки О.
Найдем, с какой величиной связано изменение вектора 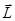 во времени:
во времени:
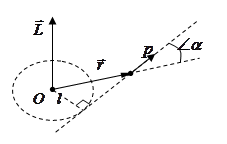
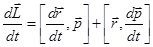 .
.
 Так как, точка О неподвижна, то
Так как, точка О неподвижна, то 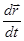 равно скорости частицы, т.е. совпадает с
равно скорости частицы, т.е. совпадает с 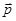 по направлению, тогда
по направлению, тогда 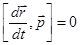 . Далее, учитывая, что
. Далее, учитывая, что 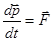 — второй закон Ньютона, получим:
— второй закон Ньютона, получим: 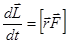 .
.
Величина  —момент силы, аксиальный вектор. Модуль
—момент силы, аксиальный вектор. Модуль 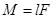 ,
, 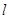 —плечо силы
—плечо силы 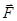 относительно т. О, рис.
относительно т. О, рис.
Таким образом, производная по времени момента импульса 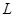 частицы относительно некоторой т. О выбранной системы отсчета равна моменту равнодействующей силы
частицы относительно некоторой т. О выбранной системы отсчета равна моменту равнодействующей силы 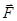 относительно этой точки
относительно этой точки
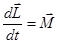 . Это уравнение называют уравнением моментов.
. Это уравнение называют уравнением моментов.
Если система отсчета является неинерциальной, то момент силы включает в себя как момент сил взаимодействия, так и момент сил инерции относительно той же т. О.
Из уравнения моментов следует что если 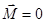 , то
, то 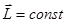 - частица совершает равномерное вращательное движение. Т.е., если момент всех сил относительно т. О системы отсчета равен нулю в течение интересующего нас времени
- частица совершает равномерное вращательное движение. Т.е., если момент всех сил относительно т. О системы отсчета равен нулю в течение интересующего нас времени 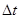 , то момент импульса частицы относительно этой точки остается постоянным.
, то момент импульса частицы относительно этой точки остается постоянным.
Уравнение моментов позволяет найти момент силы 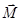 точки относительно т. О в любой момент времени, если известна зависимость
точки относительно т. О в любой момент времени, если известна зависимость 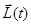 частицы относительно этой точки. Для этого достаточно продифференцировать уравнение
частицы относительно этой точки. Для этого достаточно продифференцировать уравнение 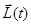 .
.
Если известна зависимость 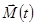 , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение
, то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение 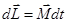 , тогда
, тогда
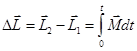
Выражение  —импульс момента силы, подобно величине
—импульс момента силы, подобно величине 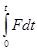 , называемой импульсом силы.
, называемой импульсом силы.
Все темы данного раздела:
Механическое движение.
Материя, как известно, существует в двух видах: в виде вещества и поля. К первому виду относятся атомы и молекулы, из которых построены все тела. Ко второму виду относятся все виды полей: гравитаци
Пространство и время.
Все тела существуют и движутся в пространстве и времени. Эти понятия являются основополагающими для всех естественных наук. Любое тело имеет размеры, т.е. свою пространственную протяженность
Система отсчета.
Для однозначного определения положения тела в произвольный момент времени необходимо выбрать систему отсчета - систему координат, снабженнуя часами и жестко связаннуя с абсолютно твердым телом, по
Кинематические уравнения движения.
При движении т.М ее координаты и меняются со временем, поэтому для задания закона движения необходимо указать вид фун
Перемещение, элементарное перемещение.
Пусть точка М движется от А к В по криволинейному пути АВ. В начальный момент ее радиус-вектор равен
Ускорение. Нормальное и тангенциальное ускорения.
Движение точки характеризуется также ускорением—быстротой изменения скорости. Если скорость точки за произвольное время
Поступательное движение
Простейшим видом механического движения твердого тела является поступательное движение, при котором прямая, соединяющая любые две точки тела перемещается вместе с телом, оставаясь параллельной| сво
Закон инерции.
В основе классической механики лежат три закона Ньютона, сформулированные им в сочинении «Математические начала натуральной философии», опубликованном в 1687г. Эти законы явились результатом гениал
Инерциальная система отсчета.
Известно, что механическое движение относительно и его характер зависит от выбора системы отсчета. Первый закон Ньютона выполняется не во всех системах отсчета. Например, тела, лежащие на гладком п
Масса. Второй закон Ньютона.
Основная задача динамики заключается в определении характеристик движения тел под действием приложенных к ним сил. Из опыта известно, что под действием силы
Основной закон динамики материальной точки.
Уравнение описывает изменение движения тела конечных размеров под действием силы при отсутствии деформации и если оно
Третий закон Ньютона
Наблюдения и опыты свидетельствуют о том, что механическое действие одного тела на другое является всегда взаимодействием. Если тело 2 действует на тело 1, то тело 1 обязательно противодействует те
Преобразования Галилея
Они позволяют определить кинематические величины при переходе от одной инерциальной системы отсчета к другой. Возьмем
Принцип относительности Галилея
Ускорение какой-либо точки во всех системах отсчета, движущихся друг относительно друга прямолинейно и равномерно одинаково:
Сохраняющиеся величины
Любое тело или система тел представляют собой совокупность материальных точек или частиц. Состояние такой системы в некоторый момент времени в механике определяется заданием координат и скоростей в
Центр масс
В любой системе частиц можно найти точку, называемую центром масс
Уравнение движения центра масс.
Основной закон динамики можно записать в иной форме, зная понятие центра масс системы:
Консервативные силы
Если в каждой точке пространства на частицу, помещенную туда, действует сила, говорят, что частица находится в поле сил, например в поле сил тяжести, гравитационной, кулоновской и других сил. Поле
Центральные силы.
Всякое силовое поле вызвано действием определенного тела или системы тел. Сила, действующая на частицу в этом поле об
Потенциальная энергия частицы в силовом поле.
То обстоятельство, что работа консервативной силы (для стационарного поля) зависит только от начального и конечного положений частицы в поле, позволяет ввести важное физическое понятие потенциально
Связь между потенциальной энергией и силой для консервативного поля.
Взаимодействие частицы с окружающими телами можно описать двумя способами: с помощью понятия силы или с помощью понятия потенциальной энергии. Первый способ более общий , т.к. он применим и к силам
Кинетическая энергия частицы в силовом поле.
Пусть частица массой движется в силов
Полная механическая энергия частицы.
Известно, что приращение кинетической энергии частицы при перемещении в силовом поле равно элементарной работе всех сил, действующих на частицу:
Закон сохранения механической энергии частицы.
Из выражения следует, что в стационарном поле консервативных сил полная механическая энергия частицы может изменяться
Кинематика.
Поворот тела на некоторый угол можно
Момент импульса и момент силы относительно оси.
Возьмем в интересующей нас системе отсчета произвольную неподвижную ось
Закон сохранения момента импульса системы.
Рассмотрим систему, состоящую из двух взаимодействующих частиц, на которые действуют также внешние силы и
Таким образом, момент импульса замкнутой системы частиц остается постоянным, не изменяется со временем.
Это справедливо относительно любой точки инерциальной системы отсчета: . Моменты импульса отдельных частей системы м
Момент инерции твердого тела.
Рассмотрим твердое тело, которое мож
Уравнение динамики вращения твердого тела.
Уравнение динамики вращения твердого тела можно получить, записав уравнение моментов для твердого тела, вращающегося вокруг произвольной оси
Кинетическая энергия вращающегося тела.
Рассмотрим абсолютно твердое тело, вращающееся вокруг неподвижной оси, проходящей через него. Разобьем его на частицы с малыми объемами и массами
Работа вращения твердого тела.
Если тело приводится во вращение силой
Центробежная сила инерции
Рассмотрим диск, который вращается вместе с шариком на пружине, надетой на спицу, рис.5.3.
Шарик находится
Сила Кориолиса
При движении тела относительно вращающейся СО, кроме , появляется ещё одна сила-сила Кориолиса или кориолисова сила
Малые колебания
Рассмотрим механическую систему , положение которой может быть определено с помощъю одной величины, например х. В этом случае говорят, что система имеет одну степень свободы.Величиной х может быть
Гармонические колебания.
Уравнение 2-го Закона Нъютона в отсутствие сил трения для квазиупругой силы вида имеет вид:
Математический маятник
Это материальная точка, подвешенная на нерастяжимой нити длиною , совершающая колебания в вертикальной плоск
Физический маятник.
Это твердое тело, совершающее колебания вокруг неподвижной оси, связанной с телом. Ось перпендикулярна рисунку и нап
Затухающие колебания
В реальной колебательной системе имеются силы сопротивления, действие которых приводят к уменьшению потенциальной энергии системы, и колебания будут затухающими.В простейшем случае
Автоколебания
При затухающих колебаниях энергия системы постепенно уменьшается и колебания прекращаются. Для того, чтобы их сделать незатухающими, необходимо пополнять энергию системы извне в определенные момент
Вынужденные колебания
Если колебательная система, кроме сил сопротивления, подвергается действию внешней периодической силы, изменяющейся по гармоническому закону
Резонанс
Кривая зависимости амплитуды вынужденых колебаний от приводит к тому, что при некоторой определенной для данной систе
Распространение волн в упругой среде.
Если в каком либо месте упругой среды (твёрдой, жидкой, газообразной) поместить источник колебаний, то из-за взаимодействия между частицами колебание будет распространяться в среде от частицы к час
Уравнение плоской и сферической волн.
Уравнение волны выражает зависимость смещения колеблющейся частицы от ее кординат ,
Волновое уравнение
Уравнение волны является решением дифференциального уравнения, называемого волновым.
Для его установления найдем вторые частные производные по времени и координатам от урав
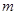 относительно точки О называется вектор
относительно точки О называется вектор 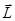 равный векторному произведению
равный векторному произведению 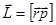 , где
, где 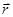 -радиус-вектор частицы,
-радиус-вектор частицы, 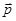 -ее импульс.
-ее импульс.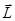 является псевдовектором. Его направление выбрано так, что вращение вокруг точки О в направлении
является псевдовектором. Его направление выбрано так, что вращение вокруг точки О в направлении 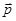 и вектор
и вектор 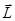 образуют правовинтовую систему. Модуль
образуют правовинтовую систему. Модуль 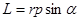 , где
, где 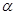 угол между
угол между 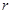 и
и  , а
, а плечо вектора
плечо вектора  относительно точки О.
относительно точки О.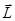 во времени:
во времени: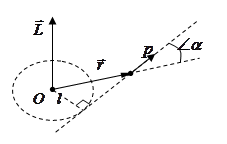
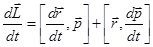 .
. Так как, точка О неподвижна, то
Так как, точка О неподвижна, то 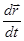 равно скорости частицы, т.е. совпадает с
равно скорости частицы, т.е. совпадает с 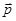 по направлению, тогда
по направлению, тогда 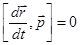 . Далее, учитывая, что
. Далее, учитывая, что 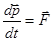 — второй закон Ньютона, получим:
— второй закон Ньютона, получим: 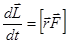 .
. —момент силы, аксиальный вектор. Модуль
—момент силы, аксиальный вектор. Модуль 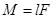 ,
, 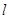 —плечо силы
—плечо силы 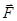 относительно т. О, рис.
относительно т. О, рис.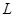 частицы относительно некоторой т. О выбранной системы отсчета равна моменту равнодействующей силы
частицы относительно некоторой т. О выбранной системы отсчета равна моменту равнодействующей силы 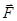 относительно этой точки
относительно этой точки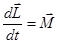 . Это уравнение называют уравнением моментов.
. Это уравнение называют уравнением моментов.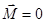 , то
, то 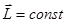 - частица совершает равномерное вращательное движение. Т.е., если момент всех сил относительно т. О системы отсчета равен нулю в течение интересующего нас времени
- частица совершает равномерное вращательное движение. Т.е., если момент всех сил относительно т. О системы отсчета равен нулю в течение интересующего нас времени 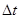 , то момент импульса частицы относительно этой точки остается постоянным.
, то момент импульса частицы относительно этой точки остается постоянным.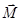 точки относительно т. О в любой момент времени, если известна зависимость
точки относительно т. О в любой момент времени, если известна зависимость 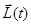 частицы относительно этой точки. Для этого достаточно продифференцировать уравнение
частицы относительно этой точки. Для этого достаточно продифференцировать уравнение 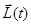 .
.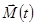 , то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение
, то можно найти приращение момента импульса частицы относительно т.О за любой промежуток времени. Для этого необходимо проинтегрировать уравнение 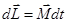 , тогда
, тогда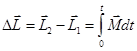
 —импульс момента силы, подобно величине
—импульс момента силы, подобно величине 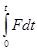 , называемой импульсом силы.
, называемой импульсом силы.






Новости и инфо для студентов