Указания к выполнению контрольной задачи К1

 

Задача К1- на определение кинематических характеристик точки по заданным в координатной форме уравнениям движения. Варианты задач различаются траекториями, которыми являются окружности, параболы, эллипсы, прямые. Все эти случаи рассмотрены в предложенных примерах 2.1-2.5. Задачи на определение кинематических характеристик точки при координатном способе задания ее движения необходимо решать в следующей последовательности:

1) выбрать систему координат;

2) исключив время из уравнений движения точки, определить уравнение траектории точки и изобразить ее график;

3) определить на графике положение точки в заданный момент времени;

4) по заданным уравнениям движения точки определить проекции скорости точки и модуль скорости по формулам (2.3) и (2.4) соответственно;

5) построить на рисунке вектор скорости точки в заданный момент времени;

6) по формулам (2.5) и (2.6) определить ускорение точки;

7) построить на рисунке вектор ускорения точки в заданный момент времени;

8) взять производную по времени от модуля скорости и составить выражение для квадрата касательного ускорения;

9) используя формулу (2.10), вычислить нормальное ускорение;

10) используя формулу нормального ускорения (2.9), вычислить радиус кривизны траектории в заданный момент времени;

11) разложить ускорение точки на касательную и нормальную составляющие на рисунке;

12) определить по касательному ускорению характер движения точки в заданный момент времени.

Пример 2.1.Движение точки М в плоскости xy задано уравнениями

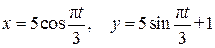(2.11)

(x, y – в см, t – в с).

Определить траекторию точки и для момента времени t₁ = 1 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.

Решение. Определим траекторию точки М, исключив из уравнений движения (2.11) время t. C этой целью приведем уравнения (2.11) к виду:

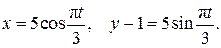
Возведем оба уравнения во вторую степень и сложим:

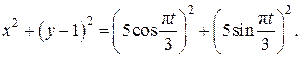
Так как 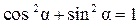, имеем уравнение вида

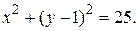(2.12)

Траекторией точки является окружность радиуса 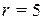с центром О₁(0,1) (рис. 2.4).

Определим начальное положение точки М₀: при t = 0

.

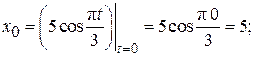
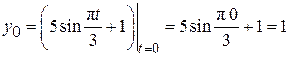В момент времени t₁ = 1 с точка М имеет координаты:

.

 

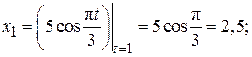
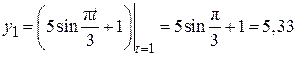Определим проекции скорости точки по формулам (2.3):

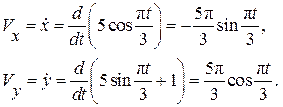(2.13)

По формуле (2.4) вычислим модуль скорости:

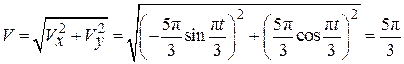. (2.14)

Определим проекции и модуль скорости в момент времени t₁ = 1 с:

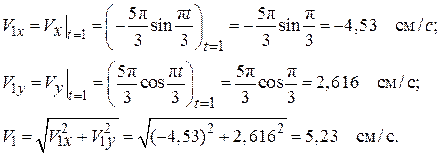
Вектор скорости строим (рис. 2.4) по составляющим:

.

 

 

Рис. 2.4

 

Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.13):

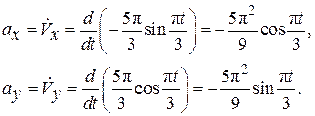
При t =1 c имеем

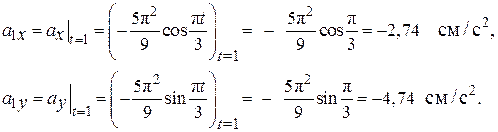
По формуле (2.6) определим модуль ускорения:

 

Вектор ускорения 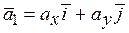направлен вниз. Найдем производную от функции скорости (2.14) по времени:

.

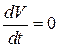При t₁ = 1 с .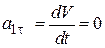

Вычислим нормальное ускорение по формуле (2.10):

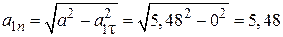см/с².

Радиус кривизны вычислим по формуле (2.9)

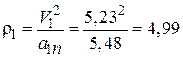см.

Следовательно, точка движется равномерно и 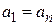. Вектор ускорения направлен к центру окружности. Совпадение расчетного радиуса кривизны окружности с радиусом окружности служит контролем правильности решения.

Пример 2.2.Движение точки М в плоскости xy задано уравнениями

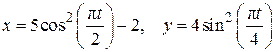(2.15)

(x, y – в см, t – в с).

Определить траекторию точки и для момента времени t₁ = 1/2 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.

Решение. Определим траекторию точки М, исключив из уравнений движения (2.15) время t. C этой целью преобразуем уравнения (2.15), приведя тригонометрические функции к одному аргументу, используя при этом тригонометрическую формулу 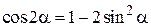. В результате получим уравнение вида

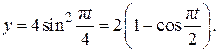(2.16)

Или

.

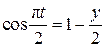Подставляя (2.16) в первое уравнение (2.15), получим 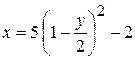или .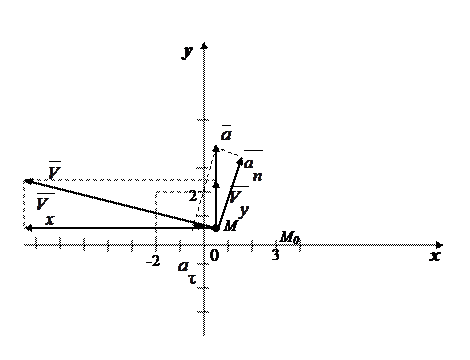

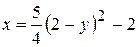Траекторией точки является парабола (рис. 2.5)

 

 

 

Рис. 2.5

 

Определим начальное положение точки М₀: при t = 0

x₀ = 5cos²0 – 2 = 3; y₀ = 4sin²0 = 0.

В момент времени t₁ = 1/2 с точка М имеет координаты:

x₁ = 5 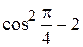= 0,5; y₁ = 4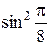= 0,59.

Определим проекции скорости точки по формулам (2.3):

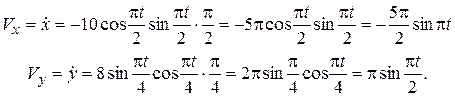, (2.17)

По формуле (2.4) вычислим модуль скорости:

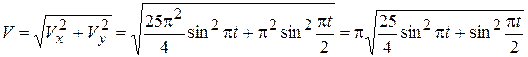. (2.18)

Определим проекции и модуль скорости в момент времени t₁ = 1/2 с:

; ;

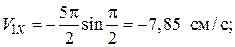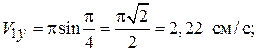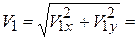
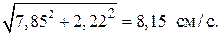
Вектор скорости строим (рис. 2.5) по составляющим:

.

Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.17):

, .

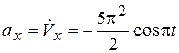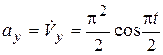По формуле (2.6) определим модуль ускорения:

.

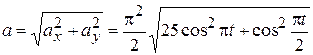При t₁ =1/2 с

, ,

 

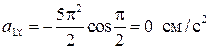следовательно, a₁ = 3,48 см/с² и вектор ускорения 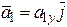направлен вертикально вверх.

Найдем производную от функции скорости (2.18) по времени:

.

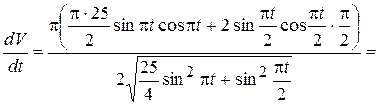
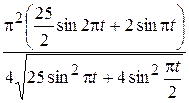При t₁ = 1/2 с .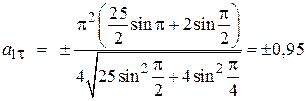

Учитывая, что 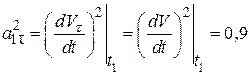, вычислим нормальное ускорение по формуле (2.10):

Радиус кривизны вычислим по формуле (2.9)

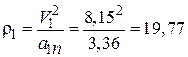см.

Разложим вектор ускорения 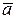на нормальную и касательную составляющие на рис. 2.5: = + .

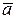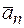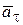Поскольку векторы скорости и касательного ускорения направлены в одну сторону, точка в данный момент времени движется ускоренно.

Пример 2.3.Движение точки М в плоскости xy задано уравнениями

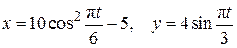(2.19)

(x, y – в см, t– в с).

Определить траекторию точки, и для момента времени t₁ = 1 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.

Решение. Определим траекторию точки М, исключив из уравнений движения (2.19) время t. C этой целью преобразуем уравнения (2.19), используя при этом тригонометрическую формулу :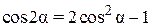

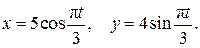
Уравнение траектории будет иметь вид

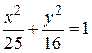. (2.20)

Для получения уравнения (2.20) использовали тригонометрическую формулу .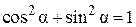

Траекторией точки является эллипс (рис. 2.6).

Определим начальное положение точки М₀: при t = 0

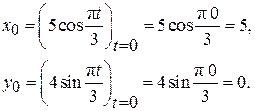
В момент времени t₁ = 1 с точка М имеет координаты:

 

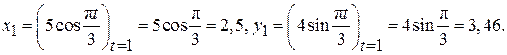
Рис. 2.6

 

Определим проекции скорости точки по формулам (2.3):

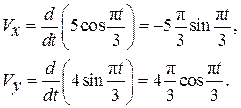(2.21)

По формуле (2.4) вычислим модуль скорости:

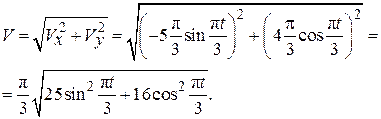(2.22)

Определим проекции и модуль скорости в момент времени t₁ = 1 с:

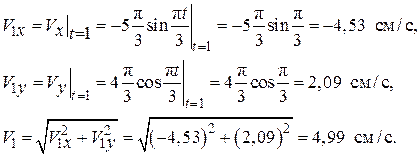
Вектор скорости строим (рис. 2.6) по составляющим:

.

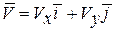Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.13):

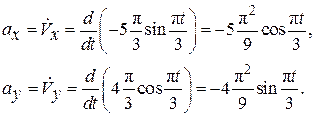
По формуле (2.6) определим модуль ускорения:

.

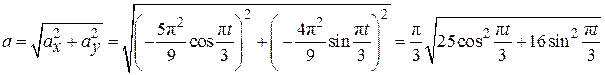При t₁ = 1 с имеем

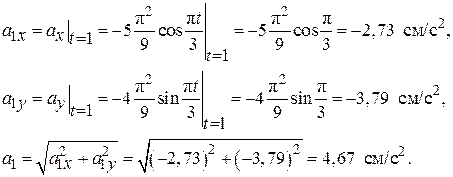
Найдем производную от функции скорости (2.14) по времени:

.

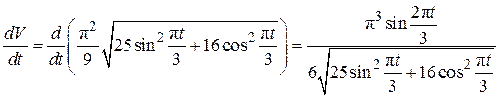При t₁ = 1 с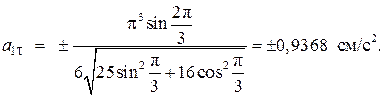

Учитывая, что 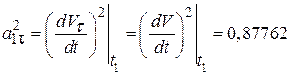, вычислим нормальное ускорение по формуле (2.10):

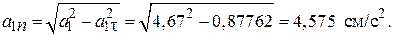
Радиус кривизны вычислим по формуле (2.9)

.

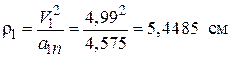Разложим вектор ускорения 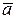на нормальную и касательную составляющие на рис. 2.6: = + .

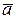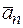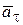Поскольку векторы скорости и касательного ускорения направлены в одну сторону, точка в данный момент времени движется ускоренно.

Пример 2.4.Движение точки М в плоскости xy задано уравнениями

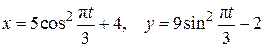(2.23)

(x, y – в см, t – в с).

Определить траекторию точки и для момента времени t₁ = 1 с, найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.

Решение. Определим траекторию точки М, исключив из уравнений движения (2.23) время t. C этой целью преобразуем уравнения (2.23) к виду

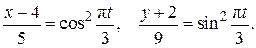(2.24)

Сложим уравнения (2.24), применив тригонометрическое тождество 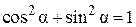, получим

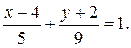
Или .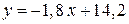

Траекторией точки является прямая (рис. 2.7)

Определим начальное положение точки М₀: при t = 0

 

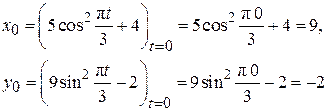
В момент времени t₁ = 1 с точка М имеет координаты:

Определим проекции скорости точки по формулам (2.3):

y

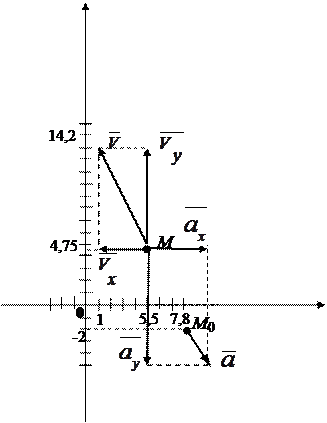
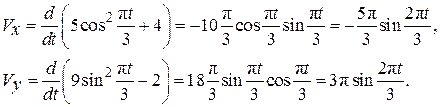(2.25)

 

Рис. 2.7

По формуле (2.4) вычислим модуль скорости:

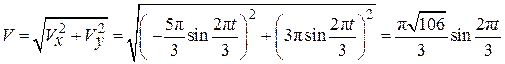. (2.26)

Определим проекции и модуль скорости в момент времени t₁ = 1 с:

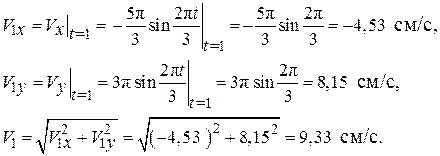
Вектор скорости строим (рис. 2.7) по составляющим:

.

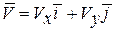Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.25):

По формуле (2.6) определим модуль ускорения:

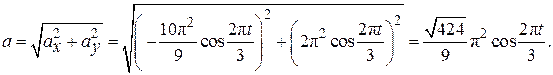
При t₁=1 с имеем

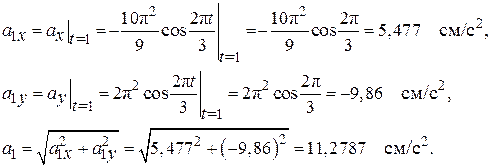
При прямолинейном движении точки радиус кривизны траектории r = µ и следовательно,

.

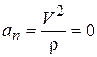Поскольку векторы скорости и ускорения направлены в разные стороны, точка в данный момент времени движется замедленно.

Пример 2.5.Движение точки М в плоскости xy задано уравнениями

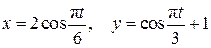(2.27)

(x, y – в см, t – в с).

Определить траекторию точки и для момента времени t₁ = 2 с найти положение точки M на траектории, ее скорость, полное, касательное и нормальное ускорения. Определить также радиус кривизны траектории в точке М.

Решение. Определим траекторию точки М, исключив из уравнений движения (2.27) время t. C этой целью преобразуем уравнения (2.27), применив тригонометрическое тождество 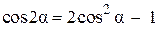к виду

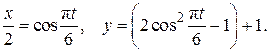(2.28)

Или

.

 

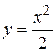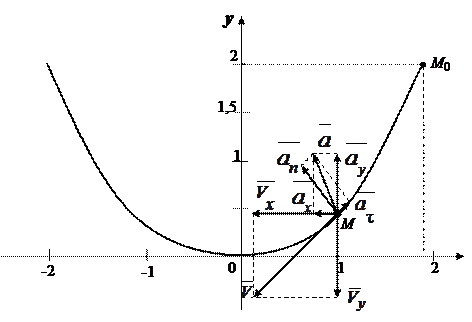траекторией точки является парабола (рис. 2.8).

 

Рис. 2.8

 

Определим начальное положение точки М₀: при t = 0

 

В момент времени t₁ = 2 с точка М имеет координаты:

 

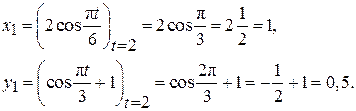
Определим проекции скорости точки по формулам (2.3):

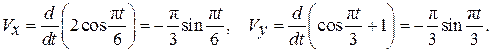(2.29)

По формуле (2.4) вычислим модуль скорости:

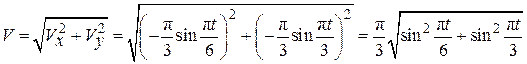. (2.30)

Определим проекции и модуль скорости в момент времени t₁ = 2 с:

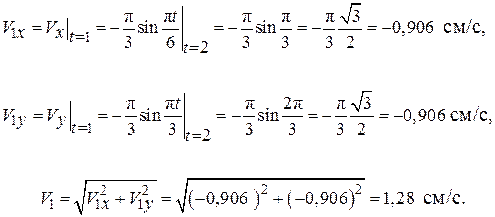
Вектор скорости строим (рис. 2.8) по составляющим:

.

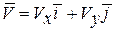Определим проекции ускорения точки М, вычисляя производные по времени от проекции ее скорости (2.29):

По формуле (2.6) определим модуль ускорения:

.

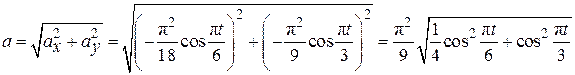При t₁ = 2 с имеем

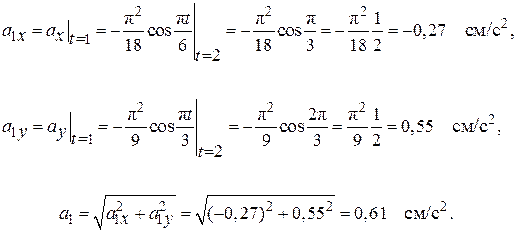
Найдем производную от функции скорости (2.30) по времени:

.

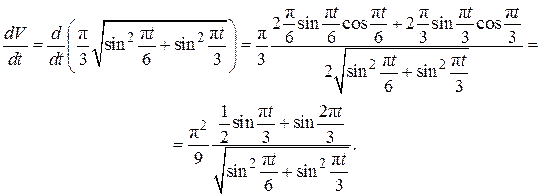При t₁ = 2 с

 

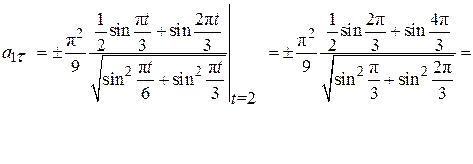
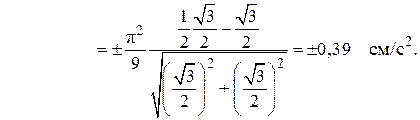
Учитывая, что 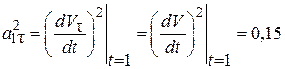, вычислим нормальное ускорение по формуле (2.10):

.

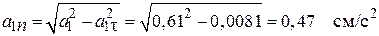Радиус кривизны вычислим по формуле (2.9)

.

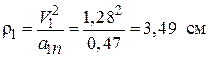Разложим вектор ускорения 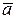на нормальную и касательную составляющие на рис. 2.8: = + .

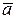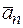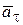Поскольку векторы скорости и касательного ускорения направлены в разные стороны, точка в данный момент времени движется замедленно.