А, в, с или x, y, z

Запись того, что элемент x принадлежит (не принадлежит) множеству X осуществляется следующим образом:

xÎX (xÏX).

В теории четких (классических) множеств может быть только две альтернативы:

xÎXлибо (xÏX).

Нечеткое множество задается следующим образом:

X — универсальное множество

A — нечеткое множество; ,

где – степень принадлежности элемента x к нечеткому множеству A.

 

 

Различают следующие виды множеств:

— конечные счетные

— бесконечные

несчетные

 

Определение 2.2. Конечное множество — это множество, состоящее из конечного числа элементов (может быть и число, и объект).

Определение 2.3. Бесконечное счетное множество — это множество, элементы которого могут быть взаимно однозначно сопоставлены элементам множества натуральных чисел.

Определение 2.4. Бесконечное несчетное множество — это такое множество элементов, которым нельзя сопоставить множество натуральных чисел.

Существуют 2 способа задания множеств:

— прямое перечисление элементов, входящих в множество (для конечных множеств);

— задание некоторых свойств, которым удовлетворяют элементы множества.

Примеры.

Правил транзитивного высказывания

Пример:

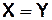, т.к. в эти множества входят одни и те же элементы.

Определение 2.8. Объединением двух множеств X, Y назовем такое множество D, для которого выполняются следующие условия.

Определение 2.9. Пересечением двух множество X и Y назовем такое множество D₂, для которого выполняются следующие условия.

Определение 2.10. Разностью двух множеств X и Y назовем такое множество D₃, для которого выполняются следующие условия.

Определение 2.11. Покрытием множества назовем семейство множеств, для которого выполняется следующее условие.

Основные операции, применяемые к множествам и их элементам:

— объединение множеств;

— пересечение множеств;

— взятие разности множеств;

— дизъюнкция (или);

—конъюнкция (и);

— квантор всеобщности (для всех);

— квантор существования (существует);

— импликация (следует);

— эквивалентность (тогда и только тогда);

— отрицание (не).

card X — мощность множества.

Для конечных множеств card B(X)=2ⁿ, где n — число элементов множества .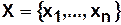

— пустое множество (множество, не содержащее ни одного элемента .

 

2.2. Основные операции над множествами.

Определение 2.5. Множество Y называется подмножеством (частью) множества X, если оно содержит только элементы, входящие в множество X.

— символ включения одного множества в другое,

— символ, обозначающий ситуации, когда одно множество является собственным подмножеством другого множества.

Определение 2.6. Множество Z называется собственным подмножеством (правильной частью) множества X, если выполняются следующие условия

.

Определение 2.7. Множества Y и X равны тогда и только тогда, когда выполняются следующие соотношения

.

Определение 2.12. Разбиением множества назовем семейство множеств, для которого выполняется следующее условие

,

 

Примеры. Дано ;

Определение 2.13. Булеаном множества X называется множество, состоящее из всех подмножеств данного множества, включая само множество и пустое множество

B(X)

 

2.3. Кортежи и декартовые произведения множеств.

Определение 2.14. Кортежем будем называть упорядоченное множество элементов

— кортеж длины n

Определение 2.15. Декартовым (прямым) произведением n — множеств вида называется множество таких всевозможных кортежей длины “n”, для которых первый элемент кортежа , второй элемент кортежа и т.д.

Замечание. Декартова плоскость, декартово произведение — частные случаи декартова произведения.

 

Определение 2.16. Если , то в этом случае декартово произведение этих множеств называется декартовым произведением или декартовой n–ой степенью ().

Примеры: ,

;

 

 

2.4. Определение отношения.

Определение 2.17.n-арным отношением называется основная математическая конструкция, записываемая в следующем виде:

,

где — базисные множества, на которых задается отношение,

— график отношения, представляющий собой некоторое подмножество декартова произведения базисных множеств (из всевозможных вариантов сочетаний множеств выбираем определенное сочетание, которое уже является описанием конкретной системы).

* Для описания реально функционирующих систем используют, как правило, не одно, а несколько отношений.

* Отношения в зависимости от «арности» бывают унарные (n=1), бинарные (n=2), тернарные (n=3), кватернарным (n=4) и т.д., а в общем случае n–арные.

* В частном случае множества, на которых строится n–арное отношение, могут быть равными , и соответственно декартово произведение этих множеств представляет собой декартову n–ю степень .

Определение 2.18. Конструкция вида , где — некоторое базисное множество отношения, n — число, определяющее арность отношения, а — график отношения называется n–арным (n-местным) отношением, заданным на множестве .

Примеры: а) — множество объектов городского хозяйства, — множество объектов городского хозяйства, которые подвергаются инвентаризации. — унарное отношение

б) — множество студентов, 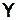— множество преподавателей, 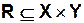— множество пар вида <студент, преподаватель>. Тогда — бинарное отношение, заданное на и 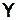, которое определяет порядок закрепления студентов за преподавателями.

в) — множество должностных лиц (элементов производства, компонент информационно-вычислительных средств), а — подмножество пар лиц (элементов производства, компонент информационно-вычислительных средств), между которыми возможен (допустим) обмен информацией. Тогда — бинарное отношение, заданное на , описывающее возможности обмена информацией между элементами .

г) — множество вещественных чисел, — подмножество точек n–мерного пространства. В этом случае n–арное отношение — может описывать совокупность точек n–мерного пространства, обладающих теми или иными свойствами, например, принадлежность некоторой произвольной кривой, поверхности, фигуре.

2.5. Формы представления бинарных отношений.

В соответствии со сформулированным выше общим определением бинарное отношение записывается в виде , где , 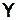— множества, на которых задается отношение, а 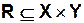— график отношения. Если пара удовлетворяет отношению 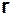и, следовательно, является элементом графика , вводятся следующие записи: или .

Частные случаи задания бинарного отношения:

а) случай полного отношения — ;

б) случай пустого отношения — .

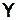Пусть и — конечные множества , . Тогда будет включать в себя пар элементов. В общем случае бинарное отношение будет включать меньшее число пар, и выделение этих пар будет базироваться на заданной содержательной интерпретации той или иной прикладной задачи.

Пример: — множество объектов городского хозяйства,
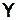— множество сотрудников проектно-инвентаризационных бюро (ПИБ), входящих в состав ГУИОН, 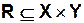— отношение, характеризующее порядок выделения сотрудников ПИБа на инвентаризацию объектов городского хозяйства.

Существует несколько способов задания бинарных отношений:

а) Прямое перечисление пар, удовлетворяющих бинарному отношению:

;

 

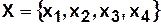б) Представление с помощью решеток с узлами.

 

в) Представление бинарных отношений с помощью булевой матрицы , m-строк, n-столбцов.

 

г) Стрелочное представление бинарных отношений.

 

д) В случае, если множество и 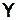— бесконечные, то может задаваться в виде аналитических выражений.

;

— эллипс на плоскости

— множество точек окружности радиуса а.

 

 

2.6. Проекции и сечения бинарных отношений. Определенность (неопределенность) и однозначность (многозначность) бинарных отношений.

При анализе свойств бинарных отношений важное значение имеет введение понятий проекции и сечения. При интерпретации бинарных отношений с помощью их представления в декартовой системе координат данные понятия приобретают известный геометрический смысл.

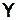Определение 2.19. Левой (правой) проекцией пары на множество (ось) () является элемент (соответственно )

,

Определение 2.20. Левой проекцией графика на множество (ось) называют такое подмножество , которое включает первые элементы пар, удовлетворяющих бинарному отношению .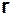

Математически это записывается следующим образом.

Левое множество (множество ) еще называется областью определения (или областью отправления) отношения .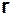

 

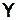Определение 2.21. Правой проекцией графика на множество (ось) называют такое подмножество , которое включает вторые элементы пар, удовлетворяющих бинарному отношению .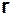

Математически это записывается следующим образом.

Правое множество (множество 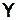) еще называется областью значений (или областью прибытия) отношения .

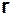Определение 2.22. Левым сечением (срезом) графика по элементу (левым сечением по ) называется множество таких элементов , для которых существуют пары .

Определение 2.23. Правым сечением (срезом) графика по элементу (правым сечением по ) называется множество таких элементов , для которых существуют пары .

Определение 2.24. Множество левых сечений графика называется фактор-множеством 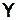по графику и обозначается , а множество правых сечений — фактор-множеством по графику (отношению 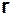) и обозначается .

Пример. ;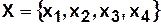

, , ,

, , ,

, ,

, .

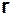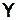Определение 2.25. Бинарное отношение называется всюду определенным слева (справа), если левая (правая) проекции графика совпадают с множеством (соответственно ). Если же имеет место (), то отношение 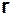является не всюду определенным слева (справа).

Определение 2.26. Бинарное отношение 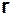называется однозначным слева (справа), если каждое левое сечение по элементам , (правое сечение по элементам , ) содержит только один элемент или пусто. Многозначность слева (справа) возникает тогда, когда хотя бы одно левое (правое) сечение содержит более одного элемента.

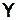Если и конечные, перечисленным свойствам бинарных отношений соответствуют следующие свойства матрицы, задающей соответствующее бинарное отношение.

 

NN п/п	Свойства бинарных отношений	Свойство матрицы, задающей бинарное отношение
1.	Определенность всюду слева	Отсутствие нулевых строк
2.	Не всюду определенность слева	Наличие нулевых строк
3.	Определенность всюду справа	Отсутствие нулевых столбцов
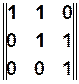
4.	Не всюду определенность справа	Наличие нулевых столбцов

 

 

NN п/п	Свойства бинарных отношений	Свойство матрицы, задающей бинарное отношение
5.	Однозначность слева	Отсутствие строк с числом единичных элементов >1
6.	Многозначность слева	Наличие строк с числом единичных элементов >1
7.	Однозначность справа	Отсутствие столбцов с числом единичных элементов >1
8.	Многозначность справа	Наличие столбцов с числом единичных элементов >1

 

 

2.7. Отображения. Частичные отображения. Мультиотображения.

Понятие «отображение» является обобщением понятия «функция», которое ранее (в курсе элементарной математики) было введено для чисел множества

y=f(x)

 

Понятие отображение уже вводится для множеств объектов.

Отображение, заданное на двух множествах, частный случай бинарного отношения

;

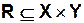
Определение 2.27. Всюду определенное слева и однозначное слева бинарное отношение 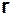называется отображением или функцией

Для отображения используются специальные формы записи:

;

Определение 2.28. Левое сечение графика по элементу называется образом элемента в

.

Определение 2.29. Правое сечение графика по элементу называется прообразом элемента в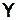

.

Определение 2.30. Не всюду определенное слева и однозначное слева бинарное отношение 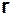называется частичным отображением (частичной функцией).

 

Определение 2.31. Бинарное отношение 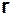всюду определенное слева и многозначное слева называется мультиотображением.

 

Определение 2.32. Бинарное отношение 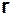не всюду определенное слева и многозначное слева называется частичным мультиотображением (частичной многозначной функцией).

 

Способы описания отображений, заданных на двух множествах такие же, что и для бинарных отношений:

- непосредственное перечисление пар,

- стрелочное представление,

- матричное представление,

- представление с помощью решетки.

Основные классы отображений

а) , 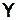— конечные множества
б) — множество вещественных чисел, — множество вещественных чисел
в) , (, отображение из 2-х мерного пространство в одномерное пространство , )

 

 

2.8. Операции над бинарными отношениями.

Графики отношений являются множествами, поэтому над ними можно производить также ранее введенные теоретико-множественные операции, как операции объединения, пересечения, взятия разности.

В отличие от обычных множеств для графиков бинарных отношений вводятся операции инверсии и композиции.

Рассмотрим все перечисленные операции

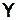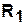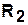Пусть , — бинарные отношения, заданные на m–элементном множестве и n–элементном множестве , а ; — булевы матрицы типа , представляющие эти отношения. В результате объединения, пересечения и взятия разности графиков и определяются бинарные отношения , , .

Для нахождения соответствующих матриц, представляющих графики указанных отношений, используются следующие процедуры:

- «объединение» матриц — почленное суммирование соответствующих элементов по правилу булева сложения 0+0=0, 0+1=1, 1+0=1, 1+1=1;

- «пересечение» матриц — почленное умножение по правилу булева умножения 0´0=0, 0´1=0, 1´0=0, 1´1=1;

- «взятие» разности матриц y —
почленное вычитание по правилу 0–0=0, 0–1=0, 1–0=1, 1–1=0.

Пример. ,

, , .

Определение 2.33. Инверсией бинарного отношения , заданного на множестве , , 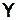называется операция построения обратного к 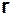отношения следующего вида , заданного на 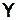, , график которого удовлетворяет условию .

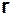Таким образом, операция инверсии сводится к замене каждой пары инверсной парой . Если отношение представлено матрицей , то отношение представляется транспонированной матрицей .

Определение 2.34. Композицией бинарных отношений , называется такое отношение , график которого удовлетворяет следующему условию .

Таким образом, операция композиции бинарных отношений и определена тогда и только тогда, когда правое множество первого отношения и левое множество второго отношения совпадают. Множество прибытия первого отношения совпадает с множеством отправления второго отношения.

Если элемент 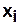связан с элементом , то это будем записывать впредь следующим образом .

Если , 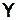конечны и графики 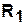, 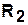заданы булевыми матрицами , , то композиция отношений и соответствует произведение указанных матриц

.

Перемножение осуществляется по правилам перемножения матриц, но при действиях над элементами используются приведенные выше правила булева сложения и умножения.

Пример. ,

; ;