Общее уравнение упругой линии сжато-изогкутого стержня

Действие распределенной поперечной нагрузки и осевой сжимающей силы. При решении различных задач по анализу устойчивости и несущей способности сжатых гибких стержней используют основные выражения перемещений при их деформации, вызванной одновременным действием сжимающей силы и поперечной нагрузки.

Применение общего уравнения упругой линии сжато-изогнутого стержня в форме метода начальных параметров позволяет значительно упростить решение ряда задач определения перемещений при одновременном действии поперечной нагрузки и продольной силы. Выведем это уравнение, используя приближенное дифференциальное уравнение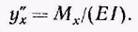: 1

(1)

Получаемое решение дает достаточно точные результаты при действии сжимающей силы S<0,85S_э, где S_э — эйлерово критиче­ское значение.

Рассмотрим сначала случай действия равномерно распределен­ной поперечной нагрузки и продольной силы S на стержень,

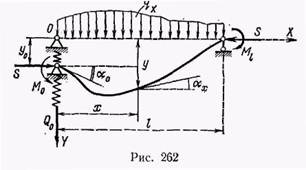
левый конец которого оперт на вертикально-податливую опору (рис. 262). На концах стержня приложены моменты М₀ и М_l. Интенсивность сплошной поперечной нагрузки q_x может меняться по степенной функции n-й степени:

(2)

Выражение (2) дает уравнение q_x в форме полинома.

На рис. 262 показана ось стержня в деформированном виде. Пренебрегая продольными перемещениями при изгибе в области малых деформаций, а также влиянием продольных деформаций сжатия, будем считать, что каждая точка оси стержня получает лишь перемещение, нормальное к первоначальной оси. Выразим ординату упругой линии у_х в функции от х, учитывая влияние продольной силы S на искривление, и, следовательно, в выраже­ние изгибающего момента М_х кроме момента от поперечной на­грузки войдет и момент силы S относительно любой точки деформированной оси. Применим следующее правило знаков: направляя ось Y вниз, ось X - вправо и помещая начало координат в центре левой опоры балки, считаем изгибающий момент М_х положитель­ным при направлении его против часовой стрелки, поперечную силу Q_x - при направлении ее вниз. Ввиду наличия левой подат­ливой опоры получаем начальный прогиб y₀. Мы имеем дело со случаем действия непрерывной нагрузки, и потому законы изме­нения у_х, у'_х, М_х и Q_x выражаются также непрерывными функ­циями.

Для получения уравнения упругой линии представим изгибаю­щий момент в произвольном сечении в виде суммы:

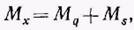
где M_q - изгибающий момент только от поперечной нагрузки; M_s = - S(y_x - у₀) - изгибающий момент от действия продольной силы.

Подставляя значение M_s, получаем полный изгибающий момент

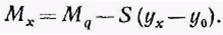(3)

Дифференцируя М_х по х, получаем согласно известному соотно­шению поперечную силу в произвольном сечении:

Первый член правой части представляет собой поперечную силу от поперечной нагрузки Q_q, второй член - поперечную силу от осевой силы S:

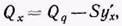(4)

где Q₄ — поперечная сила, перпендикулярная недеформированной оси.

Первая производная поперечной силы Q₄ (вызванной действием только поперечной нагрузки q_x) согласно известному соотношению из теории изгиба равна интенсивности поперечной нагрузки:

(5)

где q_x дается по уравнению (2).

Подставим теперь выражение изгибающего момента М_х из фор­мулы (3) в дифференциальное уравнение (1):

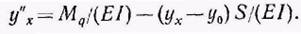
Рассматривая случай балки постоянного сечения и обозначая

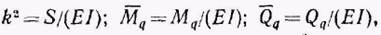(6)

получаем дифференциальное уравнение упругой линии сжато-изогнутой балки в окончательном виде:

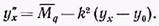(а)

При нахождении начальных значений производных у'_х, у'_х", …, у_хnпримем во внимание дифференциальные соотношения между изгибающим моментом от поперечной нагрузки и поперечной силы, а также между поперечной силой Q_q и интенсивностью поперечной нагрузки. Очевидно, при x = 0 согласно рис. 262

(б)1

В соотношениях (б) даны начальные параметры.

Интегрируя дифференциальное уравнение (а) по методу начальных параметров и вводя основную функцию решения B_х=sinkx/kU, а также учитывая интегральные зависимости между y_v, y’_v, М_х, Q_xq и т. д. по (4)-(6), получаем выражение для у_х в замкнутой форме:

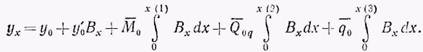(в)

Решение (в) по форме аналогично (4). Произведя подстановкой В_х и интегрирование этой функции, найдем: I

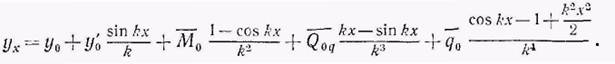(7)

Уравнение (7) впервые дано автором (1938). Это основное уравнение упругой линии сжато-изогнутого стержня при действии сплошной равномерной нагрузки, которым далее будем
пользоваться для решения различных задач.

По уравнению (7) находим общее уравнение для тангенса угла наклона упругой линии в произвольной точке ее: I

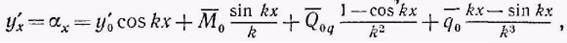(8)

где—начальный угол поворота. I

Дифференцируя уравнение (8) и умножая на EI, получаем уравнение изгибающего момента для сечения с абсциссой х: I

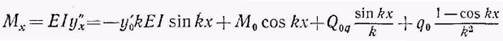, (9)

где М_о и Q_O|?—момент и перерезывающая сила от поперечной нагрузки и нормальных к оси стержня реакций. По уравнению (9) находится эпюра моментов.

Еще раз дифференцируя, находим общее выражение для попе­речной силы:

(10)

Там, где Q_x = 0, имеем экстремум для М_х. По выражению (10) можно найти место, где Q_x = Q_max.

Пользуясь найденными выражениями, легко построить эпюры у_х, у’_х, М_х, Q_x- В эти уравнения входит значение начальной поперечной силы Qoq, которое при наличии осадки опоры у₀ будет включать, ко­нечно, и дополнительную реакцию парных сил S, равную Sy_o/l. Не­трудно установить возможность применения принципа сложения влияния отдельных факторов при S = const. Выведенные общие вы­ражения применяем для отыскания ординат эпюр перемещений и эпюр усилий от действия непрерывной нагрузки и приложения со­средоточенных воздействий по концам, а также для эффективного анализа устойчивости стержней.

Пример. Определить максимальный изгибающий момент в заделанной балке от действия пары сил и осевой сжимающей силы (рис. 263, а). Момент М_о воз­никает от эксцентричного прило­жения силы M₀ = Se, где е — экс­центриситет.

Решение. Принимая начало ко­ординат в центре тяжести левого крайнего сечения и направляя ось Х по линии действия осевой си­лы после деформации, составляем выражение для тангенса угла наклона по уравнению (8):

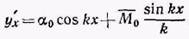
Используя условие для заделки, а
именно что при х=l; у’_х =0,

имеем

откуда получаем начальный угол наклона

Максимальный момент будет в заделке; по уравнению (9) при х = 1

Для стержня, шарнирно опертого пролетом /, в случае симметричного нагружения максимальный момент будет посередине пролета:

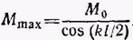
Максимальный прогиб по уравнению (17) для стержня, изображенного рис. 263, а,

Общее уравнение упругой линии при наличии прерывной нагрузки. Рассмотрим теперь действие прерывной нагрузки (рис. 263,б). В случае приложения при х=с внешних нагрузок - момента Мс сосредоточенной силы Р_с, распределенной нагрузки интенсивностью q_c — применяем метод учета скачков в аналитических функциях, известный из курса сопротивления материалов. Получаем

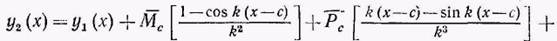
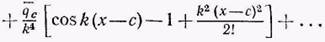(11)

Здесь влияние момента М_с, приложенного на расстоянии с от начала координат, учитывается с функциональным множителем 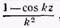, где z = х — с, причем вид этой функции тот же, что и в

уравнении (7) при начальном моменте.

Аналогично учитывается влияние скачков в поперечной силе и интенсивности нагрузки.

Соответственно уравнению (11) составляем выражения для тангенса угла наклона, изгибающего момента и поперечной силы на втором участке оси балки. I

Так, для момента имеем

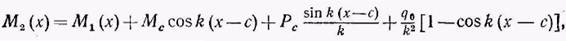
где I

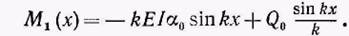(12)

Выражение (12) дает М₁{х) при х > с.

Определение критических значений сил для различных случаев.
Приведенные длины стержней. Как известно из курса сопротивления материалов, критические значения осевых сил для четырех основных случаев следующие:

для стержня, шарнирно опертого по концам,

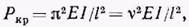
где ν= π; :

для стержня, защемленного одним концом,

где ν= 0,5π;

для стержня, защемленного одним концом, другим - шарнирно опертого,

где

для стержня, защемленного двумя концами,

где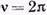

Все случаи определения критической силы могут быть сведены к основному случаю шарнирно опертого стержня введением так называемой приведенной длины /₀ = μl:

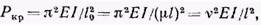(13)

где l0- приведенная длина стержня; v—коэффициент устойчивости, зависящий только от условий закрепления концов; v=kl, μ - коэффициент приведенной длины.

Выражение (13) является общим для Р_кр.

Решая соответствующее уравнение неустойчивого состояния, на­ходим коэффициент устойчивости v, зная который, вычисляем при­веденную длину данного сжатого стержня конструкции; очевидно,

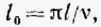(14)

после чего, зная l0из (14), находим приведенную гибкость для данного случая:

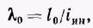
где i_ин - радиус инерции при изгибе в данной плоскости. По при­веденной гибкости можно определить коэффициент уменьшения допускаемого напряжения φ. В дальнейшем будем выражать P_кр по формуле (13) через v.