Оценивание дисперсии и среднего квадратического отклонения при неизвестном математическом ожидании

Для отыскания оценки дисперсии случайной величины необходимо знать её математическое ожидание 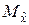. В случае, если данный параметр неизвестен, используют его оценку .

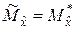Рассмотрим функцию случайной выборки в виде статистической дисперсии

, (5.2.6)

и исследуем её свойства.

1. По аналогии со случаем, когда математическое ожидание известно, можно показать состоятельность оценки (5.2.6).

2. Преобразуем выражение (5.2.6)

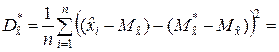
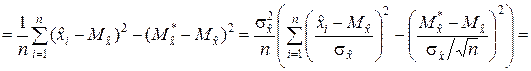
Поскольку случайные величины и 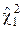являются функциями одной и той же выборки, то они зависимы. Причём их зависимость такова, что разность этих случайных величин оказывается подчинённой закону распределения хи-квадрат с n – 1 степенями свободы. Таким образом

, (5.2.7)

откуда

.

Следовательно, статистическая дисперсия оказывается смещённой оценкой параметра . Для исправления оценки её достаточно умножить на коэффициент n(n–1). С ростом объёма n выборки указанный коэффициент стремится к единице, поэтому при достаточно больших n смещённостью оценки можно пренебречь.

3. Поскольку

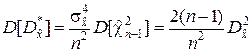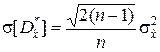, , (5.2.8)

то при n ® ¥ имеет место . Результат, полученный на основе анализа выражения (5.2.8), свидетельствует об асимптотической эффективности оценки .

Итак, при n ® ¥ исправленная статистическая дисперсия

(5.2.9)

является подходящим значением дисперсии случайной величины 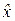. С уменьшением объёма n выборки эффективность этой оценки несколько падает.

Оценка (5.2.9) имеет следующие числовые характеристики:

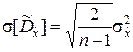; ; . (5.2.10)

Вычисление дисперсии 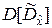связано со сложными выкладками, поэтому её выражение приведено без вывода.

При большом объёме n выборки приближённое значение оценки можно вычислять по формуле

. (5.2.11)

Перейдём к отысканию оценки для среднего квадратического отклонения 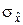случайной величины 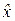в случае неизвестного математического ожидания. Указанная оценка определяется по формуле

. (5.2.12)

Проанализируем свойства оценки (5.2.12).

1. Из вышеизложенного следует, что данная оценка состоятельна и асимптотически эффективна.

2. Согласно выражениям (5.2.7) и (5.2.9) имеем

.

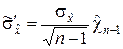Поэтому

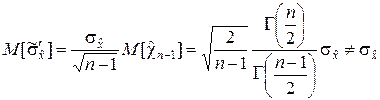
и, следовательно, (5.2.12) является смещённой оценкой 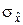. Для исправления данной оценки её достаточно умножить на коэффициент

.

Полученная при этом функция случайной выборки

(5.2.13)

будет состоятельной, несмещённой и асимптотически эффективной оценкой среднего квадратического отклонения 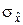случайной величины .

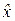Подходящее значение 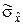можно получить и непосредственно, используя статистическую дисперсию (5.2.6). Для исправления получаемой при этом оценки 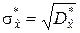её необходимо умножить на коэффициент

,

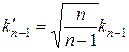т.е. величина

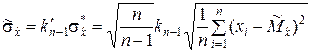
является состоятельной, несмещённой и асимптотически эффективной оценкой.

В заключение отметим, что поскольку известное соотношение для дисперсии

справедливо и для её оценки, т.е.

,

то формулам (5.2.1), (5.2.4) и (5.2.9), (5.2.11) соответственно можно придать более удобный для практического использования вид:

(5.2.14)

П р и м е р 5.6. Производятся измерения одного из габаритных размеров 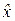однотипных деталей. Данные измерений сведены в табл.5.2.

Таблица 5.2

Результаты измерений размера деталей

i	xi	i	xi	i	xi	i	xi	i	xi
	10,5		10,4		10,3		10,5		10,8
	10,8		10,6		10,8		10,7		10,7
	11,2		10,9		10,6		10,8		10,9
	10,9		11,0		11,3		10,9		11,0

1. Найти оценку математического ожидания величины 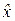и построить доверительный интервал, соответствующий доверительной вероятности b = 0,8.

2. Определить доверительную вероятность b для математического ожидания случайной величины 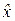, если максимальная вероятная погрешность e_b =0,07.

▼ 1. В соответствии с выражением (5.1.1) находим оценку математического ожидания

.

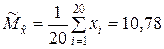По первой формуле (5.2.14) находим оценку дисперсии

.

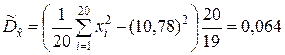Оценка среднего квадратического отклонения

.

При заданном b = 0,8 величина t_b = 1,282 (см. приложение 4), тогда максимальное вероятное отклонение математического ожидания найдём по формуле (5.1.16), что составит

.

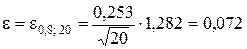Выражение (5.1.17) даёт следующий результат:

I_{0,8; 20} = [10,78–0,072; 10,78+0,072] = [10,71; 10,85].

2. В соответствии с соотношением (5.1.15) находим

.

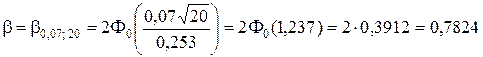Значение функции F₀(x) найдены в приложении 2.

▲

П р и м е р 5.7. Габаритный размер 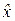деталей измеряется методом, который характеризуется дисперсий = 0,064. Определить потребный объём выборки, чтобы максимальная вероятная погрешность e оценки среднего размера деталей не превосходила 0,06 при доверительной вероятности b = 0,93.

▼ Для b = 0,93 в приложении 4 находим t_b = 1,810. Тогда из выражения (5.1.18) получаем

.

▲