Дифференцируемость и дифференциал функции

Пусть функция z=ƒ(х; у) определена в некоторой окрестности точки М₀(х₀; у₀). Составим полное приращение функции в точке М₀(х₀; у₀):

Δz=f(x₀+Δx, ₀y+Δy)–f(x₀, y₀).

Определение 1: Функция z=ƒ(х; у) называется дифференцируемой в точке М₀(х₀; у₀), если её полное приращение в этой точке можно представить в виде:

Δz=А·Δx+В·Δy+a·Δx+b·Δy,

где a=a(Δх, Δу)→0 и b=b (Δх, Δу)→0 при Δх→0, Δу→0. Сумма первых двух слагаемых в равенстве представляет собой главную часть приращения функции.

Определение 2: Главная часть приращение функции z=ƒ(х; у), линейная относительно Δх и Δу, называется полным дифференциалом этой функции и обозначается символом dz:

dz=A·Δx+B·Δy.

Определение 3: Выражения A·Δx и B·Δy называют частными дифференциалами. Для независимых переменных х и у полагают Δх=dx и Δу=dy. Поэтому равенство можно переписать в виде

dz=A·dx+B·dy.

Теорема (необходимое условие дифференцируемости функции): Если функция z=ƒ(х; у) дифференцируема в точке М(х; у), то она непрерывна в этой точке, имеет в ней частные производные dz/dx и dz/dy, причём dz/dx=А, dz/dy=В.

Обратное утверждение не верно.

Теорема (достаточное условие дифференцируемости функции): Если функция z=ƒ(х; у) имеет непрерывные частные производные в точке М(х; у), то она дифференцируема в этой точке и ее полный дифференциал выражается формулой:

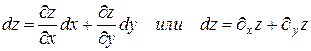
Отметим, что для функции у=ƒ(х) одной переменной существование производной ƒ¢(х) в точке является необходимым и достаточным условием её дифференцируемости в этой точке.

Чтобы функция z=ƒ(х; у) была дифференцируема в точке, необходимо, чтобы она имела в ней частные производные, и достаточно, чтобы она имела в точке непрерывные частные производные.

Арифметические свойства и правила исчисления дифференциалов функции одной переменной сохраняются и для дифференциалов функции двух (и большего числа) переменных.