рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Производная функции и ее применение к исследованию функции
Реферат Курсовая Конспект
Производная функции и ее применение к исследованию функции
Производная функции и ее применение к исследованию функции - раздел Математика, МАТЕМАТИКА Непрерывные Функции Определение 1. Функция ...
Непрерывные функции
Определение 1. Функция  называется непрерывной в точке
называется непрерывной в точке 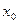 , если она определена в этой точке и некоторой ее окрестности, существует
, если она определена в этой точке и некоторой ее окрестности, существует 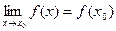 и этот предел равен значению функции в этой точке
и этот предел равен значению функции в этой точке 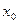 , т.е.
, т.е.
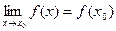 .
.
Пример. Проверим непрерывность функции 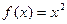 в произвольной точке
в произвольной точке 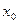 :
:
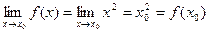 .
.
Приращением переменной величины будем называть разность между двумя ее различными значениями. Пусть в начальный момент времени переменная величина имела значение 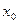 , а затем в процессе своего изменения приняла какое-то значение
, а затем в процессе своего изменения приняла какое-то значение 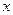 , разность
, разность 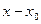 называется приращением этой переменной величины и обозначается
называется приращением этой переменной величины и обозначается 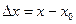 .
.
Приращение функции 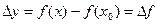 соответствует взятому приращению аргумента.
соответствует взятому приращению аргумента.
Определение 2. Функция  называется непрерывной в точке
называется непрерывной в точке 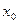 , если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента
, если она определена в этой точке и некоторой ее окрестности, и бесконечно малому приращению аргумента  соответствует бесконечно малое приращение функции
соответствует бесконечно малое приращение функции  .
.
Теорема 1. Если функции 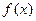 и
и 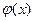 непрерывны в точке
непрерывны в точке 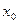 , то их сумма
, то их сумма 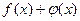 , разность
, разность 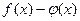 , произведение
, произведение 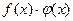 и частное
и частное 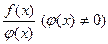 также непрерывны в этой точке.
также непрерывны в этой точке.
Теорема 2. Если промежуточный аргумент 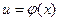 непрерывен в точке
непрерывен в точке 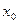 , а заданная функция
, а заданная функция 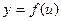 непрерывна в точке
непрерывна в точке 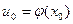 , то сложная функция
, то сложная функция 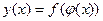 непрерывна в точке
непрерывна в точке 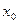 .
.
Теорема 3. Всякая элементарная функция непрерывна в любой точке своей области определения.
Если в точке 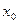 нарушены условия непрерывности функции
нарушены условия непрерывности функции 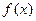 , то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
, то в этой точке функция терпит разрыв; сама такая точка называется точкой разрыва.
Определение. Предел отношения приращения функции к приращению аргумента, когда приращение аргумента стремится к нулю, называется производной этой функции
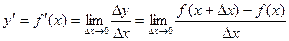 .
.
Геометрический смысл производной
Производная 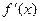 в некоторой точке
в некоторой точке 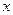 равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной в точке касания
равна угловому коэффициенту (тангенсу угла наклона) касательной, проведенной в точке касания 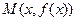 к графику функции
к графику функции  .
.
Уравнение касательной имеет вид:
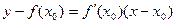
Физические интерпретации производной
Производная пути по времени = скорость движения 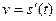 .
.
Производная скорости по времени – ускорение движения  .
.
Основные свойства производной
1. Постоянный множитель можно выносить за знак производной
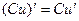
2. Производная суммы нескольких функций равна сумме соответствующих производных слагаемых
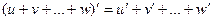
Следствие. Производная разности есть разность производных
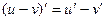
3. Производная произведения равна произведению производной первого множителя на второй плюс произведение производной второго множителя на первый
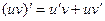
4. Дифференцирование частного:
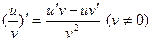
5. Дифференцирование сложной функции
Производная сложной функции по независимой переменной равна производной заданной функции по промежуточному аргументу, умноженной на производную промежуточного аргумента по независимой переменной
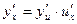
Таблица производных
1. 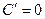 9.
9. 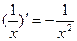
2. 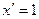 10.
10. 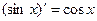
3. 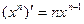 11.
11. 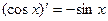
4. 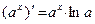 12.
12. 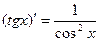
5.  13.
13. 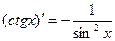
6. 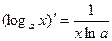 14.
14. 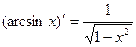
7. 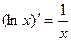 15.
15. 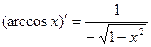
8. 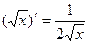 16.
16. 
17. 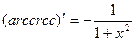
Пример 1. 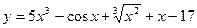
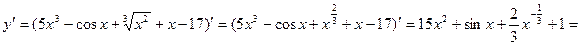
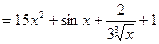 .
.
Пример 2. 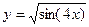
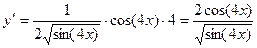 .
.
Дифференциал функции
Дифференциалом функции  в точке
в точке 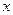 называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента
называется произведение производной функции, вычисленной в этой точке, на произвольное приращение аргумента 
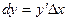 или
или 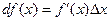
Приложения производной к исследованию функции
1. Признак возрастания и убывания функции
Теорема. Если функция  дифференцируема во всех точках какого-то интервала и ее производная
дифференцируема во всех точках какого-то интервала и ее производная 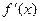 положительна в каждой точке, то функция возрастает на этом интервале. Если производная
положительна в каждой точке, то функция возрастает на этом интервале. Если производная 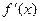 отрицательна, то функция убывает.
отрицательна, то функция убывает.
Пример. Исследовать функцию 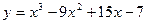
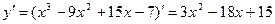

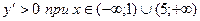 , следовательно, функция
, следовательно, функция 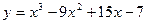 возрастает при
возрастает при 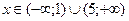 .
.
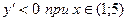 , следовательно, функция
, следовательно, функция 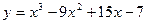 убывает при
убывает при  .
.
2. Признаки максимума и минимума.
Теорема (необходимый признак экстремума, признак Ферма). Если в точке экстремума 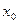 имеет производную, то производная равна нулю.
имеет производную, то производная равна нулю.
Теорема (достаточный признак экстремума). Если при переходе 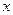 через стационарную точку
через стационарную точку 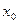 (движение слева направо) производная меняет знак с «+» на «–», то в
(движение слева направо) производная меняет знак с «+» на «–», то в 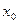 - максимум, если же с «–» на «+», то
- максимум, если же с «–» на «+», то 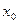 - минимум.
- минимум.
В предыдущем примере, точка 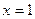 - точка максимума, точка
- точка максимума, точка 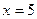 - точка минимума.
- точка минимума.
3. Наибольшее и наименьшее значения функции на замкнутом интервале
Правило отыскания наибольших и наименьших значений:
1) находим производную исследуемой функции 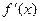 ;
;
2) определяем критические точки (решаем уравнение 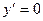 );
);
3) вычисляем значения функции в критических точках и концах интервала;
4) отбираем среди вычисленных значений самое большое и самое малое.
Пример. Найти наибольшее и наименьшее значение функции 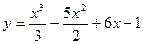 на отрезке [0,10].
на отрезке [0,10].
1) 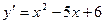 ;
;
2) 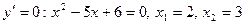 . Получили две критические точки (эти точки стационарные, разрывов у
. Получили две критические точки (эти точки стационарные, разрывов у  нет);
нет);
3) составим таблицу значений 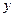 в критических точках и в концах интервала:
в критических точках и в концах интервала:
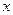
| ||||
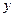
| -1 | 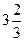
| 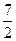
| 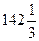
|
4) наибольшее значение 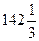 достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
достигается в правом конце интервала х=10, наименьшее значение (-1) в левом конце интервала х=0.
4. Выпуклость, вогнутость и точки перегиба кривой
Теорема. Если функция  дважды дифференцируема во всех точках какого-то интервала и ее вторая производная
дважды дифференцируема во всех точках какого-то интервала и ее вторая производная 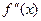 положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная
положительна в каждой точке, то это является признаком выпуклости кривой. Если вторая производная 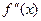 отрицательна, то кривая вогнута.
отрицательна, то кривая вогнута.
Теорема (необходимый признак точки перегиба). Если 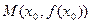 - точка перегиба, то либо
- точка перегиба, то либо 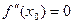 , либо
, либо 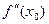 не существует.
не существует.
Теорема (достаточный признак точки перегиба). Если при переходе через точку 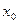 вторая производная функции
вторая производная функции 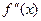 меняет знак, то
меняет знак, то 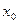 - точка перегиба.
- точка перегиба.
Пример. 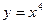
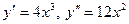 ;
;
Критическая точка: 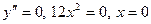
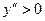 для всех
для всех 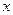 , следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
, следовательно, точек перегиба нет и кривая выпукла на всей числовой прямой.
5. Асимптоты
Прямая L называется асимптотой кривой, если расстояние от текущей точки М на кривой до прямой L становится бесконечно малой величиной, когда точка М неограниченно удаляется от начала координат (т.е. когда расстояние от М до начала координат 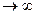 ).
).
Вертикальные асимптоты могут образовываться только в точках бесконечного разрыва функции  .
.
Пример. Определить вертикальные асимптоты функции 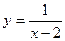 .
.
Данная функция имеет точку разрыва х=2, 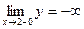 ,
,  . Таким образом, прямая х=2 – вертикальная асимптота.
. Таким образом, прямая х=2 – вертикальная асимптота.
Наклонные асимптоты
Пусть прямая L есть наклонная асимптота графика функции  . Теперь точка
. Теперь точка 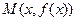 может уходить на неограниченное расстояние от начала координат, лишь когда
может уходить на неограниченное расстояние от начала координат, лишь когда 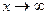 (надо, как правило, отдельно разбирать случаи
(надо, как правило, отдельно разбирать случаи 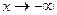 и
и 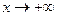 ). Уравнение наклонной асимптоты к кривой
). Уравнение наклонной асимптоты к кривой  имеет вид:
имеет вид:
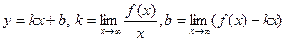 .
.
Пример. Найти асимптоты линии 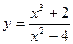
Знаменатель дроби обращается в нуль в точках 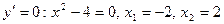 . Проверим, будут ли вертикальные прямые
. Проверим, будут ли вертикальные прямые 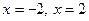 асимптотами:
асимптотами:
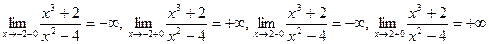 .
.
Таким образом, прямые 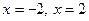 являются вертикальными асимптотами.
являются вертикальными асимптотами.
Найдем наклонные асимптоты:
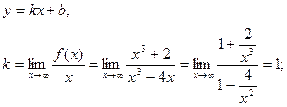
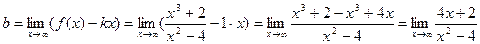 =
=
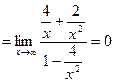 .
.
Таким образом, наклонная асимптота 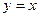 .
.
Правило Лопиталя
Теорема (правило Лопиталя). Отыскивается 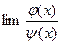 при
при 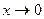 или
или 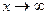 , когда одновременно
, когда одновременно 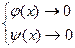 или
или 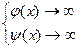 (
(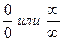 ). Если существует предел (конечный или бесконечный) отношения производных
). Если существует предел (конечный или бесконечный) отношения производных 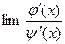 , то существует и предел отношения функций и эти пределы равны:
, то существует и предел отношения функций и эти пределы равны:
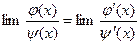 .
.
Пример.
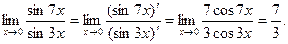
Общая схема исследования функции. Построение графика
1. Элементарное исследование: область определения; точки разрыва и интервалы непрерывности; точки пересечения графика с осями координат; симметрия графика: четность, нечетность; вертикальные и наклонные асимптоты.
2. Исследование на возрастание, убывание и точки экстремума с помощью производной функции.
3. Выпуклость, вогнутость и точки перегиба – с помощью второй производной.
4. Построение графика.
– Конец работы –
Эта тема принадлежит разделу:
МАТЕМАТИКА
бюджетного образовательного учреждения высшего... профессионального образования Московский государственный... университет экономики статистики и информатики МЭСИ...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Производная функции и ее применение к исследованию функции
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов