рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Система отсчета
Реферат Курсовая Конспект
Система отсчета
Система отсчета - раздел Механика, Механика ...
МЕХАНИКА
Введение
Физика относится к числу естественных наук, которые имеют общую задачу: изучение природы (греч. Physis – природа). Физика занимает особое место, так как предметом ее изучения являются все наиболее общие формы движения.
Движение в философском смысле – это всякое изменение: химическая реакция, электромагнитное излучение, развитие клетки, мышление. Простейшая форма движения – перемещение в пространстве – механическое движение изучается в механике. В каждом разделе физики (механика, термодинамика, электричество и магнетизм, оптика, атомная и ядерная физика) изучается соответствующая форма движения.
Деление физики на разделы производится условно для удобства изучения явлений. На самом деле все явления взаимосвязаны, поэтому связаны между собой все разделы физики, а сама физика тесно связана с другими науками. Так, например, математика дает физике аппарат исследования. Химия объясняет процессы на основе физических законов, описывающих поведение электронов в атоме. Биология использует законы физики для построения различных теорий; в последнее время возникла даже новая наука – биофизика.
Физические законы лежат в основе технических наук. Это является решающим доказательством истинности наших знаний.
Машиностроение использует законы механики, теорию тепловых процессов, электромагнитных явлений. Теплотехника, радиотехника, светотехника и другие физические направления теснейшим образом связаны с физикой. Используя законы физики, люди обеспечивают производство энергией.
Кинематика
Система отсчета
Механикаделится на кинематику (греч. сinema – движение), динамику и статику. Кинематикарассматривает движение тел в зависимости от времени, не… Динамика изучает движение тел и причины, которые вызывают это движение (греч.… Статика изучает условия равновесия тел. (греч. statike – равновесие).Траектория
с течением времени. Чтобы определить движение точки, нужно найти вид этих функций: .Совокупность последовательных поло-
процессе движения, образует в прост- ранстве линию. Эта линия называется траекторией.Кинематические характеристики поступательного движения
1) путь S, м – длина траектории (рисунок 4); 2) перемещение , м – кратчайшее расстояние между двумя положениями тела; ,Вычисление скорости и длины пути
Решение обратной задачи кинематики
В общем случае эта задача выглядит так: дана функция f(x), требуется найти такую функцию F(x), производная которой равна f(x), то есть , где (x)… Пример. Найдём первообразную от функции f(x) = x2 . Из определения следует, что является первообразной, так как .Нахождение постоянной интегрирования из начальных условий
Дано: Решение. α = const а) Нахождение зависимости скорости от времени t(0) = t0 Так как движение происходит вдоль оси 0Х, то, u = uх, α = αх. Из опреде-Графическое решение обратной задачи кинематики
Путь Графически путь равен сумме площадей 4-хугольника и треугольника /2 , т.е. . В общем случае переменного движения график скорости изобразится некоторой… Чему равен путь, пройденный телом (рисунок 2) за промежуток времени t2 – t1?Где Dt - промежуток времени, за который рассчитывается путь или средняя скорость движения.
ДИНАМИКА
ЗАКОНЫ ДИНАМИКИ
Мы переходим к динамике, основному разделу механики, который определил ее огромные успехи в развитии техники. Динамика изучает движение тел как результат взаимодействия между ними.
Основу классической механики составляют три закона Ньютона. При их изучении особое внимание следует уделить II закону Ньютона – основному закону динамики.
Первый закон Ньютона
Если же на тело не действуют другие тела, то оно остается в первоначальном состоянии. Этот опытный факт и отражает 1 закон Ньютона: существуют такие системы отсчета, в которых тело, не взаимодействующее с… При этом покой рассматривается как частный случай равномерного и прямолинейного движения .Сила
При наличии взаимодействия тел, состояние движения изменяется. Взаимодействие проявляется в изменении скорости движения тела, то есть в появлении ускорения, или, если тело покоится, в появлении деформации тел.
Мерой взаимодействия тел является сила.
Сила – это качественная и количественная мера взаимодействия тел, в результате которого тела приобретают ускорение или деформируются, или имеет место и то, и другое.
Следовательно, о наличии силы можно судить по ее динамическому проявлению (по величине и направлению ускорения) и по статистическому (по деформациям).
Взаимодействие тел может происходить как при непосредственном соприкосновении их, так и через разделяющее тела пространство (поле). К последнему относится взаимодействие масс в поле тяготения (сила тяжести), взаимодействие зарядов, токов и др.
В механике рассматривают следующие виды сил: силы упругой деформации, силы тяготения и силы трения.
Сила - величина векторная, она характеризуется численным значением, направлением и точкой приложения. Если на тело действует несколько сил, то движение происходит под действием результирующей силы, равной векторной сумме всех сил
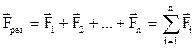 .
.
Для характеристики движущегося тела используют величину, называемую количеством движения.
Количество движения. II закон Ньютона
Количество движения есть векторная величина, равная произведению скорости движения тела на его массу
 . (15)
. (15)
Под действием сил изменяется количество движения тела. Характер этого изменения устанавливается вторым законом Ньютона:
Изменение вектора количества движения в единицу времени прямо пропорционально приложенной силе и происходит в направлении вектора силы
Это выражение справедливо, если F(t) = const. Если сила зависит от времени, то в выражении (16) необходимо перейти к пределу при Dt®0, тогда II… . Это выражение можно записать:Масса
Последняя формула позволяет выяснить смысл понятия «масса». Если на 2 тела действуют равные силы  , то
, то 
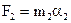 или
или  ,
,  , то есть одна и та же сила сообщает телам ускорения, обратно пропорциональные их массам. Чем больше масса тела, тем труднее изменить его состояние движения или покоя, то есть тем больше инертность тела. Инерция – свойство тел сохранять свою скорость.
, то есть одна и та же сила сообщает телам ускорения, обратно пропорциональные их массам. Чем больше масса тела, тем труднее изменить его состояние движения или покоя, то есть тем больше инертность тела. Инерция – свойство тел сохранять свою скорость.
Масса – мера инертности тела. Массу нельзя определять как количество материи.
Понятие массы более широко, Это видно из анализа зависимости массы тела от его скорости, являющейся одним из следствий специальной теории относительности
 , (18)
, (18)
где m0 - масса тела, покоящегося в данной системе координат;
с - скорость света.
При  , хотя количество вещества при этом не изменяется.
, хотя количество вещества при этом не изменяется.
Из выражения (18) следует также, что масса тела зависит от выбора системы отсчета.
Другое определение массы можно дать на основе закона всемирного тяготения
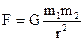
Из этого закона следует, что масса – мера тяготения или мера гравитационного взаимодействия.
Опыт показывает, что численные значения инертной и гравитационной массы с большой точностью совпадают. Таким образом, масса является универсальным свойством материи, характеризующим ее инертность и гравитационное взаимодействие.
В заключение следует отметить, что II закон Ньютона выполняется для тел, движущихся со скоростями u << с.
Третий закон Ньютона
Всякое действие тел друг на друга имеет характер взаимодействия. Силы, с которыми тела действуют друг на друга, всегда равны по величине и… . (19)Принцип относительности Галилея
Строго говоря, ИСО не существует, так как Земля, Солнце, звезды движутся ускоренно. С достаточной степенью точности ИСО связывают с Солнцем. Покажем, что все СО, движущиеся относительно ИСО с u = const, также являются… Пусть имеется ИСО xyz, а система движется вдоль оси Х с постоянной скоростью u0 (рисунок 13).Уравнения динамики не изменяются при переходе от одной ИСО к другой. Следовательно, все ИСО эквивалентны, механические явления протекают в них одинаково и поэтому никакими механическими опытами нельзя обнаружить, движется ли система прямолинейно и равномерно или находится в состоянии покоя.
В этом состоит принцип относительности Галилея. Сущность его состоит в утверждении объективности законов механики, то есть независимости от выбора СО.
СИЛЫ В МЕХАНИКЕ
, можно найти все кинематические характеристики движения тела: ускорение,… Все силы, с которыми имеет дело механика, можно разделить по природе на два основных класса:Сила тяготения
Закон всемирного тяготения
Между двумя материальными точками действует сила притяжения, пропорциональная их массам и обратно пропорциональная квадрату расстояния между ними
где - сила притяжения двух тел с массами m1 и m2 , находящихся на расстоянии r друг от друга; - гравитационная постоянная, Сила тяготения всегда направлена по линии, соединяющей взаимодействующие телаСила тяжести
, (23) где m и M3 – массы тела и Земли, R3 - радиус Земли,Космические скорости
. При движении тела вокруг Земли по окружности: R = (R3 + h) R3 = 6,4 . 106 м … man = FT или .Вес тела
Пусть тело лежит на опоре, которая неподвижна относительно Земли (рисунок 15). На тело действует сила тяжести, благодаря которой тело давит на… …ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ
Работа
1 Понятие «работа» в механике
Если сила перемещает какое-либо тело, то говорят, что она совершает работу. При постоянной силе и прямолинейном движении (рисунок 25) работу определяют как произведение пути и проекции силы на направление движения тела
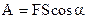 . (39)
. (39)



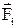
α
S 1  2 S
2 S
Рисунок 25 Рисунок 26
В общем случае криволинейного движения и переменной силы (рисунок 26) работу нужно вычислять для каждого бесконечно малого участка пути в отдельности (участок считается прямолинейным, а действующая сила – постоянной)


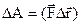 .
.
В пределе DA®dA, DS®dr, тогда dA=(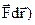 . Полная работа А силы F на участке 1-2 равна площади под кривой интегрирования
. Полная работа А силы F на участке 1-2 равна площади под кривой интегрирования
 . (40)
. (40)
Работа измеряется в джоулях: [А] = 1 Н·м = 1 Дж.
Работа консервативных сил
Консервативные силы – силы, работа которых не зависит от вида траектории, но зависит от начального и конечного положений тела. Рассчитаем работу силы тяжести , тогда (41)Мощность
Мощность Р, Вт – характеризует скорость совершения работы, 1 Вт (ватт) , (44) или, подставив значение в (44), получим еще одну формулу мощностиКинетическая энергия. Потенциальная энергия
В механике различают кинетическую энергию – функцию массы и скорости тела и потенциальную, зависящую от характера сил и конфигурации тел. Из II закона Ньютона следует, что под действием результирующей силы изменяется… . (46)Работа, всех сил, действующих на тело, равна изменению его кинетической энергии.
Кинетическая энергия измеряется в джоулях: 1 Дж = 1 Н.м.
Вывод:Кинетическая энергия 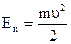 - численная (скалярная) мера механического движения тела, это функция, характеризующая состояние движущегося тела. Энергия равна максимальной работе, которую совершает сила при изменении состояния тела.
- численная (скалярная) мера механического движения тела, это функция, характеризующая состояние движущегося тела. Энергия равна максимальной работе, которую совершает сила при изменении состояния тела.
Потенциальная энергия
Потенциальная энергия Е, Дж – часть механической энергии системы, зависящая от взаимного расположения ее частиц и от характера действующих сил. Потенциальная энергия системы тел также равна максимальной работе… Выводы:Система частиц. Закон сохранения энергии
Силы взаимодействия между материальными точками системы называются внутренними. Силы, с которыми на материальные точки системы действуют внешние… Если на систему не действуют внешние силы, или их действием можно пренебречь,… Каждая частица характеризуется импульсом и энергией. Импульс системы равен геометрической сумме импульсов частицЗакон сохранения энергии
Пример 2. См. пример 1, если центр тяжести лежит по вертикали выше геометрического центра шара (рисунок 30б).
Равновесие называется безразличным, когда тело остается в равновесии в любом положении тела.
Пример 3. Однородный шар на горизонтальной плоскости. Центр тяжести и центр шара совпадают. Потенциальная энергия не меняется при любых перемещениях (центр тяжести не опускается и не поднимается) (рисунок 30в).
 |
Рисунок 30
 Закон сохранения энергии позволяет решить задачу о равновесии механической системы.. Для выяснения условий равновесия рассмотрим материальную точку с одной степенью свободы, то есть перемещение ее можно определить только одной координатой, например, х. Практически это может быть шарик, скользящий по изогнутой проволоке или по стержню на пружине (рисунки 31 и 32).
Закон сохранения энергии позволяет решить задачу о равновесии механической системы.. Для выяснения условий равновесия рассмотрим материальную точку с одной степенью свободы, то есть перемещение ее можно определить только одной координатой, например, х. Практически это может быть шарик, скользящий по изогнутой проволоке или по стержню на пружине (рисунки 31 и 32).
 |
Рисунок 31 Рисунок 32 Рисунок 33
Рассмотрим движение частицы в случае рисунка 31. Если не учитывать сил сопротивления, то движение частицы происходит только под действием сил тяжести. График зависимости потенциальной энергии от положения точки будет иметь вид (рисунок 34).
Закон сохранения энергии позволяет указать области, в которых частица с полной энергией Е находиться не может. Это области 0-х1, х2-х3, здесь Е<Еn. Проанализируем теперь движение частицы в области х1-х2. Для анализа будем использовать вывод о том, что работа консервативных сил равна убыли потенциальной энергии
 ,
,  ,
,  ,
, 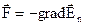 .
.
Тогда 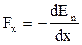 ,
,  ,
, 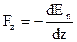 , то есть если известна
, то есть если известна  , то можно найти силу в каждой точке. В нашем примере Fx=Fr – это проекция силы тяжести на касательную к кривой Ер(х) в точке х. Пусть частица находится в точке х и движется влево. Проекция силы тяжести, действующая на нее, направлена вправо. Потенциальная энергия возрастает, а скорость уменьшается. В точке х1 E = En, то есть u = 0, но Fr ¹ 0 и частица начинает двигаться вправо. Аналогичными рассуждениями можно показать, что частица с энергией Е не может переместиться дальше х2. В точке х0
, то можно найти силу в каждой точке. В нашем примере Fx=Fr – это проекция силы тяжести на касательную к кривой Ер(х) в точке х. Пусть частица находится в точке х и движется влево. Проекция силы тяжести, действующая на нее, направлена вправо. Потенциальная энергия возрастает, а скорость уменьшается. В точке х1 E = En, то есть u = 0, но Fr ¹ 0 и частица начинает двигаться вправо. Аналогичными рассуждениями можно показать, что частица с энергией Е не может переместиться дальше х2. В точке х0  (проекция силы тяжести на касательную в точке х0 равна нулю). En = const = Emin. Частица может находиться в покое. Это условие равновесия.
(проекция силы тяжести на касательную в точке х0 равна нулю). En = const = Emin. Частица может находиться в покое. Это условие равновесия.
Область х1-х2, в которой частица оказывается запертой, называется потенциальной ямой, а область х2– х3, через которую частица не может пройти, называется потенциальным барьером.
Приведенные рассуждения вполне одинаковы для потенциальной кривой любой природы. На рисунке 34 приводятся примеры различных типов потенциальных кривых.

Рисунок 34
На рисунке 34а дана потенциальная кривая гармонического осциллятора – тела, колеблющегося на пружине. Это потенциальная яма с симметричными краями. Кривая 34б типична для взаимодействия атомов, молекул и др. Частица с энергией Е1 не может выбраться из ямы, для нее возможно только колебательное движение. При энергии Е2 связь между частицами может разорваться. На рисунке 34в изображен так называемый потенциальный ящик. Сила равна нулю (свободная частица) En =const; 
 , то есть
, то есть  , но частица не может выйти за пределы данного участка, пока полная энергия меньше высоты бортов ямы.
, но частица не может выйти за пределы данного участка, пока полная энергия меньше высоты бортов ямы.
Потенциальные кривые широко применяются в квантовой физике, а условия равновесия находят применение в технике. На основе изучения потенциальных кривых можно сделать очень важный вывод. Физическая система, предоставленная самой себе, стремится занять состояние соответствующее минимуму потенциальной энергии. Принцип минимума энергии управляет поведением механических, термодинамических и др. систем; распространяется на атомы, молекулы, кристаллы и т.д.
ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА
Вывод закона сохранения импульса
 Рассмотрим, как изменяется количество движения системы тел под действием внешних и внутренних сил.
Рассмотрим, как изменяется количество движения системы тел под действием внешних и внутренних сил.
Пусть имеется система из n тел (рисунок 35).
На каждое тело действуют внутренние силы

и внешние силы
 .
.
Под действием этих сил каждое тело
Закон сохранения импульса для центра масс
, (59) где - масса всех тел системы. Тогда из (59) следует, что .Закон изменения импульса для тел переменной массы
Ракета массой m движется со скоростью в поле силы. Продукты сгорания выбрасываются со скоростью относительно ракеты. Ежесекундный расход топлива .… - импульс ракеты в момент t, - в момент (t+dt), - импульс…КИНЕМАТИКА И ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Назначение большого класса механизмов – преобразование поступательного движения во вращательное и наоборот, поэтому знание законов вращательного…Кинематика вращательного движения
Если две точки тела закреплены, то единственно возможным движением его является… окружностей перпендикулярны оси вращения (рисунок 1).Связь линейных и угловых кинематических характеристик
. (71) Учитывая, что , то есть , получим выражение (71) в скалярной форме dr = rdj. (72)Момент силы и момент импульса
Различают момент силы относительно центра (точки) и относительно оси. Момент силы относительно точки О равен векторному произведению радиус-вектора… Или в скалярном виде , , где -плечо силы – кратчайшее расстояние от точки О до линии действия силы.Момент инерции
. (87) В случае непрерывного распределения масс суммирование сводится к… . (88)Момент импульса
. (94) Эта запись основного закона динамики вращательного движения аналогична записи… ,Работа и энергия при вращательном движении.
Работа
|
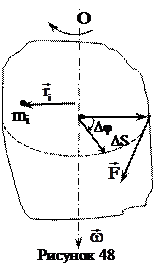 Подсчитаем работу сил, приводящих тело во вращательное движение (рисунок 48). Касательная сила
Подсчитаем работу сил, приводящих тело во вращательное движение (рисунок 48). Касательная сила  , приложенная к телу, поворачивает его на угол
, приложенная к телу, поворачивает его на угол  , при этом точка приложения силы переместится на длину дуги Ds. Работа DА силы
, при этом точка приложения силы переместится на длину дуги Ds. Работа DА силы  на пути Ds равна
на пути Ds равна
Кинетическая энергия
Кинетическая энергия тела складывается из кинетических энергий его частей . Так как - момент инерции тела, то . (99) Аналогия между кинетической энергией поступательного и вращательного движений очевидна.Применение законов сохранения импульса и момента импульса к движению
Жидкостей.
Рисунок 49 вызывает реакцию вытекающей жидкости, направленную в сторону, противоположную… Это свойство используется в водяных и паровых турбинах: струя жидкости (газа), протекая по искривленным каналам колеса…Движение тел в жидкости или газе
Поведение жидкости и газа в трубопроводе описывается уравнением Бернулли . (102) Оно показывает, что в тех сечениях потока, где его скорость возрастает, давление падает (и наоборот).Введение
Молекулярная физика изучает физические свойства и агрегатные состояния тел в зависимости от их молекулярного строения. Задачи молекулярной физики решаются методами статистики, термодинамики, молекулярной кинетики.
В основу кинетической теории положены результаты наблюдений и опытов:
1) полная хаотичность движения молекул;
2) пропорциональность средней скорости молекул корню квадратному из абсолютной температуры  ~
~  ;
;
3) средние кинетические энергии молекул разных газов, находящихся при одинаковой температуре, равны между собой, то есть  .
.
Из основных положений МКТ следует, что в газе любое направление движения равновероятно. Средние скорости молекул растут с повышением температуры газа. Для отдельных молекул различных газов, так же как и для отдельных молекул одного и того же газа, при столкновениях происходит передача энергии; скорости отдельных молекул меняются, но средние значения скоростей и энергий остаются неизменными при данной температуре.
Уравнение состояния (основное уравнение МКТ)
В молекулярной физике вводятся параметры. Которые более просто характеризуют состояние системы (газа, жидкости или твердого тела). К этим параметрам относятся: количество вещества, давление, объем, температура.
Количество вещества
Один моль – это количество вещества, в котором содержится одинаковое число структурных единиц. Это число обозначают NA и называют числом Авогадро.… . Тогда количество вещества (число молей) n равно отношению числа молекул N в данном теле к постоянной Авогадро NA, то…Давление
В газах давление обусловлено столкновением молекул со стенками сосуда. Измеряют давление манометрами, барометрами, вакуумметрами, а также различными… Кроме паскалей давление измеряется в миллиметрах ртутного столба: 1 мм рт. ст.… Подсчитаем давление, возникающее в результате удара молекул о стенки сосуда. По определению давление равно силе F,…Объем
Объем V, м3 – объем газа равен объему сосуда, в котором газ находится.
Температура
В настоящее время применяют только две температурные шкалы – термодинамическую и международную практическую, градуированные соответственно в… В международной практической шкале температура замерзания и кипения воды при… Термодинамическая шкала использует одну реперную точку – это тройная точка воды (температура, при которой лед, вода и…Уравнение Клапейрона-Менделеева
Уравнение состояния идеального газа
, (14) где В – коэффициент, зависящий от массы газа и его молярной массы. В 1874 г. Д.И. Менделеев вывел уравнение состояния для 1 моля идеального газаЧисло степеней свободы молекулы. Распределение энергии молекулы по степеням свободы
Средняя кинетическая энергия поступательного движения молекул
. (18) С другой стороны . (19)Число степеней свободы
½ kT. Z Для определения положения двухатомной молекулы… C(x,y,z) Для многоатомной молекулы (как для твердогоРаспределение энергии молекулы по степеням свободы
В случае не слишком низких температур выполняется теорема Больцмана: средняя энергия, приходящаяся на одну степень свободы молекулы, равна . Из теоремы Больцмана следует, что при одинаковой температуре средняя энергия,… Если газ идеальный, то его внутренняя энергия U равна лишь кинетической энергии хаотичного движения ,Динамические и статистические закономерности. Распределение Больцмана. Функции распределения. Реальные газы
Динамические и статистические закономерности
В молекулярной физике рассматриваются явления, вызванные взаимодействием колоссального количества частиц. Каждая молекула газа в секунду испытывает… Благодаря огромному числу соударений молекулы за очень короткий промежуток…Распределение Больцмана
Если же молекулы находятся в силовом поле, например, в поле силы тяжести, то давление будет меняться. Предположим, что температура по всему объему… Если на высоте h выделить площадку S, то на нее будет действовать сила F ,Функции распределения
Но почему же на большей высоте меньше молекул? Потому что на высоте h = 0 есть молекулы, движущиеся слишком медленно, чтобы… Таким образом, пользуясь уравнением (32), можно получить функцию распределения молекул по скоростям ,Распределение Максвелла
. (34) Уравнение (34) можно привести к виду . (35)Флуктуации. Реальные газы. Уравнение Ван-дер-Ваальса. Фазовые переходы
Флуктуации
Случайные хаотичные изменения числа молекул, плотности и ряда других величин называются флуктуациями (от латинского fluctuation – колебание). Роль… , а также среднее значение этих отклоненийРеальные газы. Уравнение Ван-дер-Ваальса
Чтобы найти уравнение состояния реального газа, нужно определить, как взаимодействие молекул влияет на давление. Рассмотрим взаимодействие двух… Из рисунка видно, что при r > r0 взаимная потенциальная энергия… Fоm – силы отталкивания;Фазовые переходы
ЯВЛЕНИЯ ПЕРЕНОСА
Во время развития кинетической теории газов против неё делались возражения такого рода: если скорости движения молекул действительно порядка… Вспомним, что средняя длина свободного пробега молекул зависит от концентрации… (45)Диффузия
. Выразим j через средние величины скорость , длины пробега и концентрацию… .Рисунок 15 Рисунок 16
Диффузия – взаимное проникновение молекул соприкасающихся веществ вследствие их теплового движения. Распространение запаха – тоже одно из проявлений диффузии.
Диффузия происходит даже в твёрдых телах. И это явление используют для получения примесной проводимости полупроводников. Предположим, что концентрация молекул изменяется вдоль координаты х (рисунок 16) а в плоскости zy остаётся неизменной. Температура T , а следовательно средняя скорость хаотичного движения 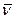 , по всему объёму одинакова.
, по всему объёму одинакова.
Тогда плотность потока (46) для диффузии можно представить как
 , (47)
, (47)
где 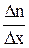 - градиент концентрации.
- градиент концентрации.
Знак « - » показывает, что перенос происходит из слоя с большей плотностью в слой с меньшей плотностью.
Учитывая, что 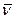 и
и  являются в данных условиях постоянными, поток диффузии запишется:
являются в данных условиях постоянными, поток диффузии запишется:
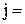
 . (48)
. (48)
Плотность потока диффузии j пропорциональна градиенту концентрации 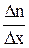 , перенос происходит в сторону выравнивания концентраций.
, перенос происходит в сторону выравнивания концентраций.
Коэффициент перед градиентом называют коэффициентом диффузии:
 ,
, 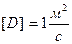 . (49)
. (49)
Коэффициент диффузии зависит от 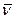 и
и  , которые зависят от температуры. Таким образом, можно показать, что
, которые зависят от температуры. Таким образом, можно показать, что  ~
~ , то есть коэффициент диффузии возрастает с ростом температуры и уменьшением концентрации.
, то есть коэффициент диффузии возрастает с ростом температуры и уменьшением концентрации.
Умножив (48) на массу молекулы mi , получим закон Фика – закон диффузии
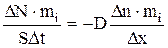 . (50)
. (50)
Учитывая, что  масса перенесённого вещества, а
масса перенесённого вещества, а  - плотность вещества, закон диффузии примет вид:
- плотность вещества, закон диффузии примет вид:
 . (51)
. (51)
Закон Фика (51) применим только для небольших перепадов плотности. Если изменение плотности происходит очень быстро, то коэффициент диффузии  , так как средняя длина свободного пробега изменяется вследствие заметного изменения концентрации. Диффузия приводит к выравниванию концентраций, то есть приводит систему к равновесному состоянию.
, так как средняя длина свободного пробега изменяется вследствие заметного изменения концентрации. Диффузия приводит к выравниванию концентраций, то есть приводит систему к равновесному состоянию.
Вязкость
Вязкость возникает при относительном перемещении слоёв жидкости или газа. Молекулы, участвуя в хаотичном движении,…Теплопроводность. Применение закономерностей явлений переноса в технике
При тепловом движении молекул происходит выравнивание температуры за счёт переноса молекулами кинетической энергии. Закон теплопроводности был… Энергия, переносимая N молекулами через поверхность S за время будет равна , (57)ТЕРМОДИНАМИКА
ПЕРВЫЙ ЗАКОН ТЕРМОДИНАМИКИ. ИЗОПРОЦЕССЫ
Термодинамика – это учение о связи и взаимопревращениях различных видов энергии, теплоты и работы.
Термодинамика, в отличие от статистической физики, не рассматривает конкретные молекулярные картины. На основании опытных данных формулируются основные законы, часто называемые основными принципами или началами термодинамики.
Первый закон термодинамики.
Одним из основных понятий термодинамики является понятие термодинамической системы. Термодинамической системой называется совокупность тел, которые… Математически термодинамические процесс описываются несколькими функциями,…Внутренняя энергия
Внутренняя энергия (твердого тела, газа и др.) U, Дж включает кинетическую энергию молекул, энергию межмолекулярного взаимодействия, энергию… U = Ек мол+ Еп мол+ Еат+ Еяд+ Еизл. (1) Последние три компоненты вносят незначительный вклад, поэтому ими можно пренебречь.Работа
Совершение работы сопровождается перемещением внешних тел, воздействующих на систему. Так, например, при движении поршня в цилиндре, при изменении объема газа совершается работа
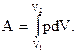 (3)
(3)
Это легко доказать. Элементарная работа при перемещении поршня на расстояние Dh (рисунок 2) равна DA = FDh, так как SDh = DV – приращение объема.
Полная работа при изменении объема от V1 доV2 равна интегралу (3). При совершении работы происходит упорядоченное движение молекул системы, которое приводит к изменению внутренней энергии.
Работа, в отличие от внутренней энергии. уже не является функцией состояния системы, так как зависит от вида процесса (рисунок 1).
Работа определяется площадью под кривой интегрирования
DАa>DАb>DAc.
В пределе DA переходит в dA - частный дифференциал : 

Количество теплоты
При теплообмене изменение внутренней энергии происходит за счет изменения неупорядоченного (хаотического) движения молекул: молекулы более нагретого тела при взаимодействии передают часть энергии молекулам более нагретого тела. Количество энергии, переданной телу путем теплообмена без совершения работы, называют количеством теплоты.
Первый закон термодинамики
По закону сохранения энергии приращение внутренней энергии системы должно быть равно сумме совершенной работы над системой и количества сообщенного… (4.1) Часто это выражение записывают в видеТеплоемкость
Одно и то же количество теплоты, сообщенное разным телам, вызывает не одинаковое изменение температуры тел. Говорят, у тел разная теплоемкость.… Теплоемкость – количество теплоты, которое необходимо сообщить телу для… . (6)Изопроцессы
Изохорный процесс
Изопроцесс – процесс, протекающий при каком-либо постоянном параметре системы:Изобарный процесс
Изменение внутренней энергии . Работа . Первый закон термодинамики (9) . Молярная теплоемкость тогда .Изотермический процесс
T = const, уравнение изотермы pV = const. Изменение внутренней энергии DU = 0, так как DТ = 0. Работа . (11)Адиабатный процесс
, (12) то есть работа совершается за счет убыли внутренней энергии газа. Прежде чем подсчитать работу адиабатного процесса, найдем уравнение состояния для адиабатного процессаКруговые процессы (циклы)
Круговой процесс считается обратимым, если все его части обратимы. Различают прямой цикл и обратный. Прямой цикл (рисунок 5а) совершается в тепловой… Работа за цикл равна площади между линиями перехода. Одной из основных характеристик цикла является его КПД. Тепловая машина превращает тепло в работу, иначе говоря,…Цикл Карно
1-2 – изотермическое расширение за счет тепла от нагревателя Т1; 2-3 – самопроизвольное адиабатное расширение за счет внутренней…ВТОРОЙ ЗАКОН ТЕРМОДИНАМИКИ
Первое начало термодинамики выражает всеобщий закон сохранения и превращения энергии. Однако, он не может описать все явления природы, так как не… Второе начало термодинамики, в частности, устанавливает теоретические границы…Необратимые процессы. Энтропия
Все реальные процессы неравновесные, однако изучение их имеет исключительно большое значение, т.е. позволяет найти пути максимального приближения… Процесс называется обратимым, если возможно осуществить обратный переход… Любой процесс, сопровождаемый трением, является необратимым, ибо при тренииЭнтропия
Для определения степени необратимости процессов необходимо сравнение их
с идеальными – обратимыми.
Равенство Клаузиуса.
или , . Считая количество отданной теплоты Q2 отрицательным, получимЭнтропия обратимого цикла
С учетом (20) и (21) получим: изменение энтропии в обратимом цикле равно нулю . (22) Функция S была названа энтропией тела. Каждое состояние тела характеризуется определенным значением S. Для обратимого…Энтропия необратимого цикла
то есть , , так как Q2 < 0, то (23) сумма приведенных теплот меньше нуля. В любом реальном цикле (процессе) можно выделить обратимую и необратимую части,…Свободная энергия. Энтальпия
Понятие энтропии широко используется в теплотехнических расчетах. При этом обычно пользуются основным уравнением термодинамики (26), полученным из 1 закона путем замены dQ на TdS
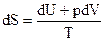 . (26)
. (26)
Свободная энергия
или . (27) Величина U – T·S называется свободной энергиейтермодинамической… обозначается F. Таким образом,Связанная энергия
Внутреннюю энергию U можно представить в виде двух слагаемых
U = ( U - T·S ) + T·S = F + T·S, (29)
где T·S – связанная энергия, та часть внутренней энергии, которая не может быть использована для совершения работы.
Энтальпия
(30) Величину (31) Называют энтальпией, которая является функцией состояния системы.Второй закон термодинамики и его философский смысл
Существует несколько эквивалентных формулировок II –го начала термодинамики
Второй закон термодинамики
Это означает, что для такого перехода теплоты требуется совершение работы внешними телами, что осуществляется, например, в холодильной машине.… Физический смысл II-го закона термодинамики наиболее ясно раскрывается в… В справедливости такой формулировки легко убедиться, вспомнив цикл Карно, КПД которого равенФилософский смысл II закона термодинамики
Это порождало метафизические и теологические гипотезы. При этом не учитывалось, что II закон термодинамики не является абсолютным по двум причинам.…ОСНОВЫ СПЕЦИАЛЬНОЙ ТЕОРИИ ОТНОСИТЕЛЬНОСТИ
Введение
Законы классической механики справедливы лишь при малых скоростях движения. Изучение законов движения с субсветовыми скоростями (u~с) привело к коренной ломке наших физических представлений. Существенное изменение претерпевали представления о пространстве и времени. Совершенно новое освещение получила такая характеристика материи, как масса и ее связь с энергией. Сами законы движения получили новую формулировку. Как известно механический принцип относительности утверждает, что никакими механическими опытами внутри инерциальной системы отсчета нельзя установить ее состояние равномерного и прямолинейного движения. Естественно поставить вопрос, нельзя ли решить этот вопрос с помощью физических опытов.
Специально поставленные опыты Майкельсона дали отрицательный ответ. Изменение скорости распространения света вдоль направления движения Земли по орбите и перпендикулярно дали одинаковые значения. Это говорит о том, что скорость света не зависит ни от направления наблюдения, ни от скорости движения источника и наблюдателя.
Опыты по измерению скорости света позволили обобщить классический принцип относительности и на этой основе построить новую теорию относительности.
Теория относительности была создана А.Эйнштейном в 1905 г. Специальная теория относительности (СТО) рассматривает явления в инерциальных системах отсчета. Системы отсчета, движущиеся с ускорением рассматриваются в общей теории относительности (ОТО).
Основным в СТО являются постулаты Эйнштейна и преобразования координат Лоренца.
Постулаты СТО. Преобразования Лоренца
Первый постулат:все физические явления в ИСО при одинаковых начальных условиях протекают одинаково. Другими словами среди ИСО нет «привилегировнных»… Второй постулат:скорость света в вакууме во всех ИСО одинакова, причем… Как видим, первый постулат – это просто обобщение принципа относительности Галилея, распространение его на все законы…Следствия СТО
Относительность длин
В СТО длина относительна. Будем называть собственной длиной тела его длину в той системе отсчета, где оно покоится. Пусть в штрихованной системе… , , , , . (3)Понятие одновременности
, , . (4) Таким образом, в системе О эти два события будут одновременны лишь при условии…Относительность временных интервалов
, , , , . (5) Сравните (5) с (3): так как b < 1, то Dt > Dt0, то есть в системе О прошло больше времени, чем в . Длительность…Правило сложения скоростей
. Из постулатов Эйнштейна и преобразований Лоренца получается другой вариант… ; ;Масса и энергия
Чтобы закон Ньютона удовлетворял требованиям СТО и при больших скоростях, его запись надо видоизменить так ). Если обозначить то запись закона сохраняется, но смысл m изменяется. Если в классической механике считалось, что масса…– Конец работы –
Используемые теги: система, отсчета0.028
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Система отсчета
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


 , но
, но 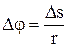 , следовательно
, следовательно  ,
где
,
где  - момент касательной силы
- момент касательной силы  .
.
 .
Работа, совершаемая при повороте тела на конечный угол j будет
.
Работа, совершаемая при повороте тела на конечный угол j будет
 . (98)
. (98)





Новости и инфо для студентов