ДВИЖЕНИЕ ЧАСТИЦЫ В ПЕРИОДИЧЕСКОМ ПОЛЕ

 

Рассмотрим очень важную для физики твердого тела, а значит и для физики низких температур, задачу о движении частицы в периодическом поле с потенциалом

 

V(r+n) = V(r),

где

n= n₁a₁ + n₂a₂ + n₃a₃

 

причем a_1,a₂,a₃- тройка некомпланарных векторов, а n₁, n₂, n₃ - произвольная тройка целых чисел. Нас интересуют стационарные состояния и энергетический спектр (общие закономерности), т.е. надо исследовать стационарное уравнение Шредингера

 

y(r) = E y(r),

где

= /2m+, = -i²Ñ².

 

Ранее мы вводили одномерный оператор трансляции

 

(a) = e^{i/i pa},

 

который действует так:

(a)y(x) = y(x+a)

и

^-1(a)() (a) = (-), (⁺= 1 Þ ⁺= ^-1).

Его обобщение на трехмерный случай очевидно:

 

(n)= e^i/ipn,

 

причем здесь в качестве n выбран уже вектор трансляции, по которому есть периодичность. Для потенциала имеем:

 

^-1(n)V(r)(n)= V(r-n) =V(r),

откуда

V(r)(n)= (n)V(r),

 

т.е. оператор трансляции коммутирует сV(r):

 

X(n)V(r)] = .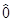

 

Кроме того, он коммутирует с (это всегда - см. выше):

 

= ,

 

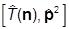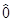а значит

= ,

 

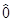и потому оператор порождает интеграл движения.

По этой же причине могут быть выбраны общие собственные функции операторов и , т.е. стационарные состояния будут характеризоваться не только значениями энергии, но и собственными значениями оператора трансляции:

 

y(r) = t(n) y(r).

 

Применим к этому уравнению оператор :

 

y(r) = t*(n)t(n) y(r).

 

Но так как = , то слева стоит просто y, а потому

 

|t(n)| = 1,

 

т.е. t(n) есть некий фазовый множитель (это следствие унитарности ):

 

t(n) = e^i/iqn.

Величина q называется квазиимпульсом ( по понятным причинам). В отличие от обычного импульса, квазиимпульс определен неоднозначно. Можно сделать замену