ЧЕТНОСТЬ

 

Мы получили, что волновые функции стационарных состояний осциллятора являются или четными или нечетными. Оказывается, этот результат можно было предсказать заранее, не решая задачу. Сделаем в этой связи отступление, которое представляет и значительный самостоятельный интерес.

Рассмотрим преобразование пространственной инверсии системы координат

r ® r’ = -r

и введем оператор пространственной четности , действующий на волновые функции в координатном представлении по закону

 

Y (r) = Y (-r).

Рассмотрим теперь функцию

 

j(r) = (r) Y (r)

 

и подействуем на нее оператором :

 

j(r) = ,

 

откуда

(r) = (-r).

 

В частности, если гамильтониан есть четная функция r, а для этого достаточно, чтобы таковой была потенциальная энергия:

 

V(-r) =V(r) Þ (-r) = (r),

 

то из предыдущего он будет коммутировать с оператором четности:

 

[,] = 0,

 

а значит будет интегралом движения.

Докажем, что оператор описывает некоторую динамическую переменную (она называется пространственной четностью). Для этого надо доказать, что он эрмитов. Имеем:

 

(Y(r),Y(r)) = Y^*(r) Y(r)dV =

 

=Y^*(r) Y(-r)dVY^*(-r) Y(r)dV =

 

={Y^*(r)}^* Y(r)dV=(Y,Y),

 

что и утверждалось. Найдем возможные значения этой наблюдаемой, т.е. собственные значения P оператора :

 

Y_p = PY_p.

 

Действуем еще раз оператором :

 

{Y_p (r)} = {PY_p()}.

 

Слева получим

 

{Y_p(r)} = Y_p (-r) = Y_p(r),

 

а справа

 

{PY_p(r)} = P{Y_p(r)} = P{PY_p(r)} = P²Y_p(r).

Таким образом,

 

Y_p(r) = P²Y_p (r),

откуда

P = ± 1.

 

Таким образом, у оператора имеется лишь два собственных значения, которым соответствуют четные и нечетные собственные функции:

P = +1: Y₊(-r) = + Y₊(r),

 

P = -1: Y_- (-r) = - Y_-(r).

 

Эти собственные значения также называются четностью (пространственной, так как в физике элементарных частиц используют и другие четности).

Если четность есть интеграл движения, т.е.

 

[,] = 0,

 

(см. выше), то из

 

Y_E = EY_E

следует

(Y_E) = () Y_E = ()Y_E = 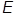(Y_E) = (Y_E)

 

Таким образом, если Y_E - волновая функция стационарного состояния с энергией 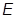, то таковой будет и функция Y_E. Если энергетический спектр простой (невырожденный), т.е. если каждому 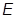отвечает одна (с точностью до множителя) волновая функция, то и Y_E должны быть пропорциональны друг другу:

 

Y_E = PY_E,

 

а это значит, что Y_E есть собственная функция оператора , т.е. обладает определенной четностью.

Вывод: если гамильтониан есть четная функция координат, то он коммутирует с оператором , т.е. - интеграл движения; если к тому же энергетический спектр - простой, то каждое стационарное состояние обладает определенной четностью, т.е. его волновая функция или четна, или нечетна.

Для одномерного гармонического осциллятора все условия выполняются: потенциальная энергия четна, а энергетический спектр - простой (в одномерном случае дискретный спектр всегда простой). Поэтому волновые функции стационарных состояний осциллятора - четные или нечетные.