КОГЕРЕНТНЫЕ СОСТОЯНИЯ

 

Вектор основного состояния |0ñ - собственный вектор оператора с собственным значением 0:

 

|0ñ = 0 º 0|0ñ.

 

Поставим задачу на отыскание всех собственных векторов оператора :

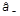|añ = a|añ.

 

Найдем векторы |añ в n- представлении, для чего разложим их по базису {|nñ}:

|añ = án|añ|nñ,

 

и определим коэффициенты разложения án|añ. Для этого умножим уравнение на собственные значения оператора слева на án:

 

án|_-|añ = aán|añ.

Расписываем левую часть:

 

án|_-|añ = ,

 

и приходим к рекуррентному соотношению

 

án + 1||añán|añ,

 

решение которого очевидно:

 

án + 1|añ=á0||nñ

 

В результате искомое разложение принимает вид:

 

.

 

Величину á0|añ находим из условия нормировки:

 

1 = áa|añ = á0|añ^*á0|añ,

(ám|nñ = d_mn).

 

Откуда, с точностью до произвольного фазового множителя,

 

á0|añ = .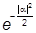

 

Таким образом, для собственных векторов |añ оператора окончательно получаем

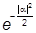
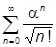|añ = |nñ,

 

где |nñ - векторы стационарных состояний осциллятора. Нетрудно доказать, что этот ряд сходится при любом aÎС, т.е. спектр оператора заполняет всю комплексную плоскость, и у него имеется континуум собственных векторов. Удивляться не надо, ибо - неэрмитов оператор, а спектральные свойства таких операторов могут быть весьма непривычными. Например, у оператора , наоборот, нет ни одного собственного значения и ни одного собственного вектора.