КОГЕРЕНТНЫЕ СОСТОЯНИЯ

Л Е К Ц И Я 9

КОГЕРЕНТНЫЕ СОСТОЯНИЯ

Продолжение

Чтобы найти волновые функции состояний a в координатном представлении, можно умножить обе части последней формулы слева на |xñ и учесть,… áx |añ = ya(x), áx|nñ = yn(x).  

СМЕШАННЫЕ СОСТОЯНИЯ И МАТРИЦА ПЛОТНОСТИ

До сих пор мы описывали состояния микросистемы векторами гильбертова пространства |yñ и волновыми функциями y(q) в каком-то заданном… Начнем с достаточно простого случая системы двух частиц 1 и 2. Для системы из…  

РЕЗЮМЕ

Чистое состояние можно задавать как вектором |yñ, так и статистическим оператором 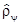(матрицей плотности).

Свойства статистического оператора :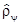

1. Как и всякий оператор, он есть эрмитов оператор:

= .

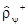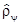2. Статистический оператор - положительный:

 

.

 

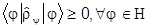Действительно,

 

.

 

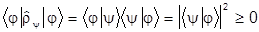3. Диагональные матричные элементы его лежат в интервале (0,1):

 

.

 

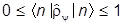Это сразу следует из того, что

 

án|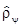|nñ = |án|yñ|² º |y_n|².

 

Справа величина неотрицательная, а сумма всех таких величин 1.

 

4. След статистического оператора равен 1:

 

Sp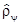= 1.

 

Действительно,

 

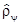Sp= Sp(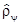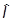) = áy |I|yñ = áy |yñ = 1.

 

5. Статистический оператор чистого состояния - идемпотентный:

 

.

 

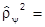
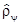Это следует из того, что двойное проектирование ничего нового не дает.

6. Статистический оператор подчиняется уравнению

= .

 

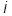
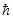
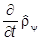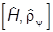Это следует из его определения и из уравнения Шредингера:

=

=

 

=-= .

 

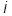
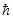
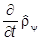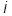
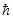
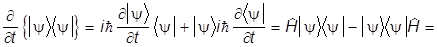
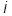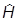
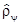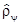
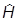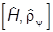Проведенное рассмотрение делает естественным следующее обобщение.

Основной постулат квантовой механики

Произвольное состояние квантовомеханической системы описывается статистическим оператором 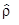общего вида, т.е. некоторым эрмитовым положительным оператором с единичным следом:

 

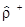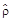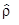= , ³ 0, Sp 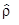=1.

 

Физический смысл смешанных состояний, т.е. состояний, описываемых статистическими операторами общего вида, устанавливает следующее важнейшее утверждение:

Всякий статистический оператор может быть представлен как

= ,

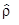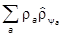где 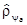- статистические операторы (проекторы) чистых состояний 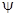, а 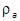- числа со свойствами

r_a³0, 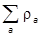= 1.

Доказательство основывается на математическом результате, что всякий эрмитов оператор с конечным следом (такие операторы называются ядерными) имеет чисто дискретный спектр. Ставим задачу на собственные значения

 

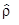|y_añ = r_a |y_añ,

где числа r_a вещественны (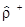= 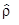), а векторы |y_añ - ортонормированы

 

áy_a|y_a^’ñ = d_aa

 

и образуют базис:

=.

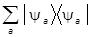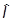Умножаем обе части уравнения справа на áy_a|, суммируем по а и учитываем разложение единицы:

 

= .

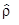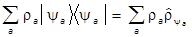Для чисел r_a имеем:

r_a º r_a áy_a|y_añ = áy_a|r_a|y_añ = áy_a|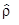|y_añ ³ 0,

 

где использовано уравнение на собственные значения и положительность .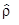

Наконец, вводя произвольный ортонормированный базис, найдем:

 

 

= ,

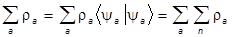
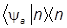
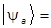
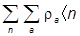
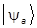
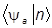
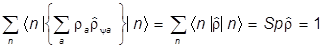и утверждение доказано.

В основной постулат входит, разумеется, тот же способ вычисления средних значений в произвольном состоянии, что и для чистых состояний:

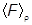= Sp().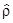

 

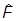Преобразуем эту формулу:

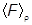= Sp(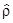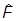) = Sp= ,

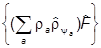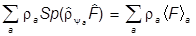т.е.

= .

 

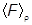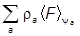Отсюда проистекает великий смысл смешанных состояний. Они соответствуют ансамблю, т.е. множеству копий одной и той же системы, каждая из которых находится в каком-то квантовом состоянии y_a, но не известно, в каком именно. Об этом мы можем судить лишь вероятностно, причем вероятность того, что при измерении F мы «наткнемся» на систему в состоянии y_a равна как раз r_a. Тогда среднее значение F в смешанном состоянии будет вычисляться как средневзвешенное отдельных средних 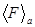с весами r_a:

 

r_a ³ 0, 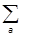r_a = 1.

 

Обычная терминология здесь такая. Если у статистического оператора 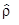есть хотя бы два различных собственных значения 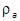, то состояние называется смешанным. Если же у него есть только одно собственное значение (тогда оно равно 1), то состояние - чистое. Последнее естественно, ибо тогда 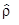сводится к 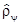, а мы видели, что задание 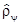- один из возможных способов описания обычных (чистых) состояний.

Если состояние смешанное, то при вычислении средних приходится проводить двоякое усреднение. Первое из них (слагаемые 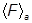в последней формуле) - специфическое квантовомеханическое усреднение, от которого никуда не денешься. Оно присуще уже чистым состояниям и не имеет классического аналога. Второе усреднение (суммирование по а с весами r_a) проводится по ансамблю и связано лишь с неполнотой описания. Мы с ним встретились в изначальном примере, когда искусственно выщепили одну частицу из единой двухчастичной системы. Такое усреднение не является специфическим для квантовой механики. Оно присуще уже классической физике и составляет основу любого статистического подхода. Поэтому в квантовой механике главенствующая роль принадлежит именно чистым состояниям. А смешанные состояния широко используются в квантовой статистике, а также при описании поляризационных свойств пучков частиц (например, фотонов при наличии у света частичной поляризации).

И в заключение одно замечание технического характера. Найдем квадрат статистического оператора:

 

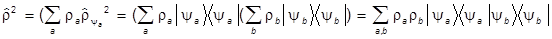
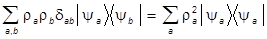= , т.е.

 

.

 

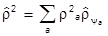Шпур находим сразу, учитывая, что Sp(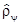) = 1:

 

Sp .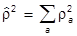

 

А теперь вспомним, что

 

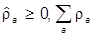= 1.

 

Если состояние чистое, то отлично от нуля только одно 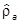, причем оно есть 1. Поэтому для чистого состояния

 

Sp 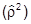_чист = 1.

 

Для смешанного состояния есть несколько ненулевых 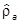. Каждое из них меньше 1, а потому 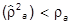. Это значит, что

 

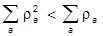= 1,

 

т.е. для смешанного состояния

 

Sp.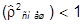

 

В итоге получен критерий, позволяющий определить, не решая задачу на собственные значения оператора 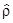, описывает ли он чистое состояние, или смешанное.