ОРБИТАЛЬНЫЙ МОМЕНТ ИМПУЛЬСА

 

Дальше мы намерены перейти к анализу движения частицы в центральном поле. Как и в классической физике, здесь очень важную роль играет момент импульса. Но в квантовой механике бывает два момента импульса - связанный с движением частицы и имеющий классический аналог, и не связанный с движением частицы, собственный момент, не имеющий классического аналога. Первый называется орбитальным, второй - спином. Сейчас будем рассматривать только орбитальный момент импульса.

В классической механике

L= r´p.

 

Эта формула переносится и в квантовую механику, но для операторов:

 

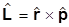
В декартовых координатах в r-представлении компоненты имеют вид:

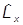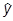
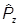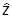
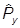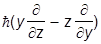
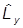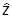
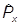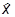
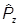=- = -i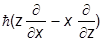

 

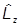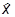
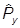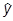
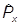=-= -i

 

=-= -i.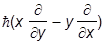

 

Это можно записать единообразно:

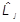= i.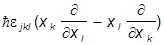

 

Здесь e_jkl --символ Леви-Чевита: антисимметричен по всем индексам и нормирован условием e₁₂₃ = +1. Компоненты с разными значками отличны от нуля, а если хотя бы одна пара одинаковых индексов, то равны 0. При этом

e₁₂₃ = e₃₁₂ = e₂₃₁ = +1, e₂₁₃ = e₃₂₁ = e₁₃₂ = -1.

 

Используя коммутации

 

 

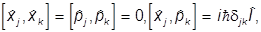
легко показать, что

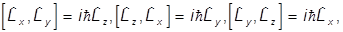
т.е.

 

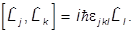
Важную роль играет оператор квадрата момента

 

=++,

 

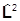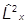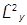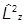который коммутирует с операторами компонентов момента:

 

 

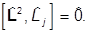
Дальнейший анализ удобно проводить в сферических координатах

 

x = rcosjsinq, y =rsinjsinq, z =rcosq.

 

Довольно нудные выкладки по замене переменных дают:

 

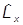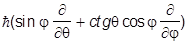
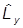= i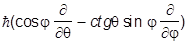

 

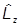= -i

 

= -i.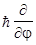

 

Особенно важным является последнее соотношение. Проверим его

 

 

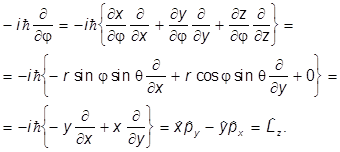
Не менее важен оператор .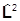

В сферических координатах он с точностью до множителя совпадает с угловой частью оператора Лапласа:

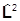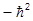= Ñ_q,j² = -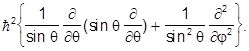

 

Напомним, что полный оператор Лапласа есть

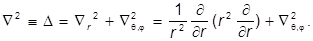
Все операторы момента содержат только q и j, но не r. Поэтому их собственные функции могут содержать любую зависимость от r, которая нас не интересует. Считаем поэтому, что все происходит на сфере единичного радиуса, а потому

 

y = y(q,j).

 

Ставим задачу на отыскание общих собственных функций взаимно коммутирующих операторов 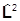и :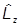

 

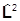y(q,j) = L²y(q,j)

 

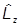y(q,j) = L_zy(q,j)

 

и вводим обозначения

L² = l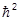, L_z = m,

 

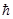так что в явном виде уравнения запишутся как

 

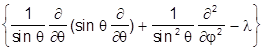y(q,j) = 0

 

-i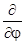y(q,j) = my(q,j).

 

Решения должны быть: непрерывными, конечными и однозначными. В курсе математической физики доказывается, что решения нашей задачи существуют только при

 

l = l(l+1), где l = 0,1.2,...

 

и m =m, где m- целые числа из интервала -l£ m £l.

 

Таким образом, каждому неотрицательному целому l отвечает 2l+1 независимых решения с разными m.

Они называются сферическими функциями (гармониками) и имеют вид

y_lm(q,j) = Y_lm(q,j) =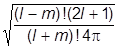P_l^m(cosq)e^imj,

 

присоединенные полиномы (хотя и не полиномы) Лежандра

P_l^m(z) = (1-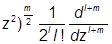(z²-1)^l, m>0.

 

и выражаются через обычные полиномы Лежандра:

P_l^m (z) = (1-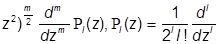(z²-1)^l.

Сферические гармоники образуют ортонормированную систему функций на сфере единичного радиуса:

 

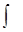dWY _lm^* (q,j)Y_l’m’(q,j) = d_ll’d_mm’,

где

dW = sinqdqdj

 

есть элемент телесного угла (или элемент площади сферы с R=1). Кроме того, на этой сфере они образуют базис, так что

y(q,j) = 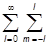C_lmY_lm(q,j), C_lm =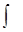dWY _lm^* (q,j)y(q,j).

 

Сферические функции обладают свойством

 

Y _lm^* (q,j) = (-1)^m Y _lm (q,j).

 

Итак, мы установили, что орбитальный момент квантуется. Квадрат его принимает значения

 

L² = 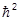l(l+1), l = 0,1,2,...

 

а проекция на ось z - значения

 

L_z = 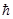m, -l £ m £ l