рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- ВАРИАЦИОННЫЙ МЕТОД
Реферат Курсовая Конспект
ВАРИАЦИОННЫЙ МЕТОД
ВАРИАЦИОННЫЙ МЕТОД - раздел Механика, ВАРИАЦИОННЫЙ МЕТОД Еще Один Мощный Метод Нахождения Низших Энергетических Уровне...
Еще один мощный метод нахождения низших энергетических уровней - вариационный метод. Рассмотрим функционал
J(y,y*) = áy| |yñ =
|yñ = 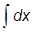 y*(x)
y*(x) y(x),
y(x),
где x – весь набор переменных. Функции y предполагаются нормированными:
áy|yñ = 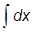 y*(x) y(x) = 1.
y*(x) y(x) = 1.
Решаем задачу на условный экстремум, т.е. ищем функции, доставляющие функционалу экстремум при дополнительном условии нормировки. Используем метод Лагранжа, т.е. требуем
d{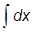 y*(x)
y*(x) y(x) - l
y(x) - l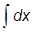 y*(x) y(x)} = 0,
y*(x) y(x)} = 0,
или
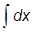 {dy*(
{dy*( y - ly) + (y*
y - ly) + (y* - ly*)dy} = 0.
- ly*)dy} = 0.
Поскольку dy* и dy считаются независимыми вариациями, то экстремумы достигаются на функциях y, удовлетворяющих уравнениям
 y = ly,
y = ly,  y* = l*y*.
y* = l*y*.
Видим, что условие экстремума есть стационарное уравнение Шредингера, если отождествить l = E. Поскольку  - эрмитов оператор, то l* = l, и уравнения для y и y* эквивалентны - получаются друг из друга операцией комплексного сопряжения (
- эрмитов оператор, то l* = l, и уравнения для y и y* эквивалентны - получаются друг из друга операцией комплексного сопряжения ( - вещественный оператор). Таким образом, вместо того, чтобы решать уравнение Шредингера, можно искать функции, которые доставляют экстремум функционалу J.
- вещественный оператор). Таким образом, вместо того, чтобы решать уравнение Шредингера, можно искать функции, которые доставляют экстремум функционалу J.
Покажем, что абсолютный минимум функционалу J дает волновая функция основного состояния. Возьмем собственные функции гамильтониана
 jn = Enjn, ájn|jmñ = dnm,
jn = Enjn, ájn|jmñ = dnm,
и разложим по ним произвольную функцию y:
y =  anjn.
anjn.
Из условия нормировки следует, что
 |an|2 = 1.
|an|2 = 1.
Подставляем разложение в функционал:
J = áy| |yñ =
|yñ =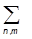 an*amájn|
an*amájn| |jmñ =
|jmñ = 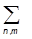 an*am Emdnm =
an*am Emdnm =  En|an|2.
En|an|2.
Пусть E0 - энергия основного состояния, тогда En ³ E0, и
J =  En|an|2 ³ E0
En|an|2 ³ E0 |an|2 = E0 Þ J³E0.
|an|2 = E0 Þ J³E0.
Но, если y = j0, то
J = E0.
Таким образом, функционал J имеет минимум, и он достигается именно на функции j0. Это его минимальное значение равно E0 , что и составляет основу вариационного метода при отыскании энергии основного состояния.
На вариационный метод позволяет найти и следующие энергетические уровни. Пусть нашли E0 как минимум функционала, достигаемого на функции y=j0. Будем искать энергию E1 и функцию j1 из условия минимума функционала при дополнительных ограничениях
áy|yñ = 1, áy|j0ñ = 0.
Доказательство почти такое же, как в предыдущем случае. Имеем
J = áy| |yñ =
|yñ =  En|an|2,
En|an|2,
где по-прежнему
 |an|2 = 1,
|an|2 = 1,
но теперь из условия áy|j0ñ=0 следует a0=0, и потому
J =  En|an|2³ E1
En|an|2³ E1 |an|2 = E1.
|an|2 = E1.
Таким образом,
J ³ E1,
причем минимум достигается на y=j1.
Высшие энергетические уровни находятся аналогично. Значение En находится как минимум функционала на функциях, подчиненных условиям
áy|yñ = 1, áy|jnñ = áy|j1ñ = ... = áy|jn-1ñ = 0.
До сих пор рассмотрение было точным, но решение вариационной задачи обычно не проще, а сложнее непосредственного решения уравнения Шредингера. Но есть еще приближенный метод, и очень эффективный, - прямой вариационный метод, или метод Ритца. В этом методе экстремумы ищутся не на всем множестве квадратично интегрируемых функций, а только на пробных функциях, принадлежащих весьма узкому классу. А именно, выбирают функции какого-то заданного вида, но зависящие от некоторого числа параметров:
y = y(x|a, b, ...) .
Тогда и функционал
J = áy|yñ = y*(x|a, b, ...)
y*(x|a, b, ...) y(x|a, b, ...)dx = J(a, b, ...),
y(x|a, b, ...)dx = J(a, b, ...),
будет функцией этих параметров, и отыскание его экстремума сводится к отысканию экстремума функции нескольких переменных a, b, ..., а это весьма простая задача из области обычного математического анализа. Если пробные функции заранее нормированы (а это всегда делают), то минимум будет находиться из решения системы обычных уравнений
 = 0,
= 0,  = 0,...,
= 0,...,
откуда получаются значения a0, b0,..., для которых, как следует из строгого рассмотрения, всегда
J(a0,b0,...) ³ E0.
Если класс пробных функций выбран удачно, то можно приближенно положить
E0 = J(a0,b0,...), j0 = y(x½a0,b0,...).
Главное искусство, таким образом, выбор подходящего класса пробных функций. Здесь нужно использовать всю наличную информацию, дополняя ее интуицией. Следующие уровни находятся, как описано выше. Функция y берется из того же класса, но не только нормированной, но и ортогональной к приближенной функции j0 основного состояния, уже найденной. Практически метод используют для нахождения нескольких нижних уровней, так как с ростом номера уровня резко возрастают вычислительные трудности из-за множества дополнительных условий.
Пример. Попробуем найти энергию основного состояния атома водорода с гамильтонианом
 =
=  -
-  .
.
В основном состоянии l=0, а потому в сферических координатах волновая функция зависит только от r , но не от q и j :
y = y(r).
Она должна очень быстро стремиться к нулю при r ® 0, а потому можно попытаться положить
y = Pn(r)e -br,
где Pn(r) - некоторый полином, а b - варьируемый параметр. Но в вариационном исчислении доказывается, что функция, доставляющая минимум функционалу, не может иметь нулей в конечной области (а функция, доставляющая (n+1)- й экстремум, имеет n нулей - это теорема об узлах). Поэтому для волновой функции основного состояния полином Pn должен быть просто константой, и множество пробных функций есть
y(r½b) = Аe -br, b>0.
Дальше будут полезны интегралы
In(b) º  ,
,
которые получаются дифференцированием по b основного интеграла
I0(b) º  .
.
Находим константу А из условия нормировки:
1 = dVy*y =
dVy*y = r2dr
r2dr dWy*(r) y(r) = 4pA2
dWy*(r) y(r) = 4pA2 r2dre-2br = 4pA2I2(2b) =
r2dre-2br = 4pA2I2(2b) =
= 4pA2 =
= 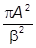 ,
,
откуда
А =  y(r½b) =
y(r½b) =  e -br.
e -br.
Вычисляем функционал J(b). Учитывая, что
Ñ2 (e -br) = 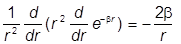 e -br + b2e -br
e -br + b2e -br
получим (элементарные выкладки с использованием In опускаем)
J(b) =  e -br(
e -br( -
- )e -br =
)e -br =  .
.
Ищем минимум
0 = ,
,
где а-радиус Бора. Для приближенной волновой функции основного состояния получаем
y0(r) =  .
.
Энергия основного состояния приближенно вычисляется как J(b0):
E0 = J(b0) =  ,
,
т.е.
E0 = - .
.
На самом деле результаты получились точными. Это потому, что слишком уж хорошую выбрали пробную функцию. Если бы взяли
y(r½b) = А e -br ,
,
то результаты получились бы значительно хуже.
В качестве полезного упражнения предлагается решить аналогичную задачу для одномерного гармонического осциллятора
 =
=  ,
,
взяв как раз пробные функции вида
y(x½b) =А e -bx , b>0.
, b>0.
– Конец работы –
Эта тема принадлежит разделу:
ВАРИАЦИОННЫЙ МЕТОД
На сайте allrefs.net читайте: ВАРИАЦИОННЫЙ МЕТОД.
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ВАРИАЦИОННЫЙ МЕТОД
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов