ОСНОВЫ КВАЗИРЕЛЯТИВИСТСКОЙ КВАНТОВОЙ ТЕОРИИ

Будем искать релятивистские поправки к нерелятивистской квантовой физике. В последовательной релятивистской квантовой теории возможны процессы рождения частиц, которые в рамках нашего курса не могут быть учтены, почему мы и говорим не о релятивистской квантовой теории, а о релятивистских поправках к нерелятивистской квантовой теории, или о квазирелятивистском приближении.

Дальше будет очень полезным следующий эвристический способ «вывода» уравнения Шредингера. Берем классический гамильтониан свободной частицы

H =

заменяем в нем классические величины по правилу

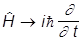, p® -iÑ

и действуем полученными операторами на волновую функцию:

 

iy.

 

Ясно, что это уравнение не обладает свойством релятивистской инвариантности. При переходе к другой системе отсчета энергия и квадрат импульса преобразуются по-разному. В уравнении Шредингера стоит первая производная по времени, но вторые производные по координатам, а время и пространственные координаты в теории относительности должны быть формально равноправны.

Напомним основные положения специальной теории относительности (СТО). Пространство Минковского состоит из 4-векторов

 

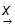= (x⁰,x¹,x²,x³),

где

x⁰ = ct, а {x¹,x²,x³} = x

 

есть обычный 3-вектор. Верхние индексы отвечают контравариантным компонентам векторов. Можно перейти к ковариантным векторам и наоборот по правилу

 

x_n = g_nlx^l , xⁿ = g^nlx_l ,

 

где g - метрический тензор:

g^mn = g_nm = .

 

Скалярное произведение в пространстве Минковского вводится как

 

() = y₀xⁿ = g_nlyⁿx^l = g^nly_nx_l = x⁰y⁰ - (x,y),

 

и оно является 4-скаляром, или инвариантом преобразований Лоренца. В частности, скалярный квадрат самого 4-вектора 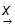записывается как

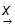()² = (x⁰)² - x².

 

Преобразования Лоренца есть как раз линейные преобразования, сохраняющие скалярные квадраты 4-векторов:

 

x^¢m = L^m_nxⁿ, (^¢,^¢ ) = (,)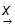

 

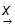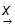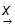откуда нетрудно получить основное свойство матрицы Лоренца

 

LgL^T = g.

Преобразования Лоренца описывают переход от одной инерциальной системы отсчета к другой (вращения и движения, но не трансляции). В частности, если штрихованная система отсчета движется относительно исходной вдоль общей оси x¹=x со скоростью V, то матрица Лоренца такова:

L = , b .

 

В СТО энергия E и импульс p объединяются в 4-вектор

 

= (p⁰,p¹,p²,p³),

где

 

p⁰ = , (p¹,p²,p³) = p.

 

При преобразованиях Лоренца

 

p^m ®p^¢m = L^m_npⁿ_.

 

Квадрат 4-импульса есть инвариант:

 

pⁿ p_n = ()² - p² = m²c² = inv,

 

где m - масса частицы (в последовательной теории это есть ее определение!). Преобразование Лоренца сохраняет 4-скалярные произведения, в частности

 

p^mx_m = p^¢mx^¢_m.

 

Вернемся к квантовой теории. Начали с подстановок

H ® i, p® -iÑ,

 

которые теперь можно объединить в ковариантную подстановку

p^m ® iÑ^m, Ñ^m º .

 

В частности, если взять релятивистское выражение для энергии

 

E =

 

и сделать в нем эти подстановки, получим нечто вроде релятивистского обобщения уравнения Шредингера

 

iy.

 

Но здесь непонятно, что такое корень из оператора. Правда, его можно попытаться разложить в ряд Тейлора, но тогда возникнут производные сколько угодно высокого порядка - тоже нехорошо. Связь 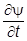с y(r) не будет локальной, и фактически выписанное уравнение, как можно показать, есть интегральное уравнение. От такого уравнения отказываемся, так как и соответствующая теория пока не построена (формально ее можно построить и некие ее результаты даже используются, но ничего хорошего на этом пути не получается).

Будем действовать по другому, исходя из выражения не для самой энергии, а для ее квадрата:

 

E² = p²c² + m²c⁴.