рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Ускорение. Нормальное и тангенциальное ускорение.
Реферат Курсовая Конспект
Ускорение. Нормальное и тангенциальное ускорение.
Ускорение. Нормальное и тангенциальное ускорение. - раздел Механика, Ускорение. Нормальное и тангенциальное ускорение Скорость При Движении Тел Может Меняться К...
Скорость при движении тел может меняться как по величине, так и по направлению( рис. 3.1):

 изменение скорости за время
изменение скорости за время  t.
t.
Определение ускорения :
 (3.1)
(3.1)
Т.к.
|
 (3.2)
(3.2)
Ускорение равно первой производной от скорости или второй производной от радиус - вектора по времени.
Ускорение характеризует быстроту изменения вектора скорости. Оно направлено так же как  при
при  . Из рис. 3.1 видно, что вектор
. Из рис. 3.1 видно, что вектор  направлен в сторону “закругления” траектории. Подставим в (3.1) вектор
направлен в сторону “закругления” траектории. Подставим в (3.1) вектор  , выражен через его проекции (уравнение (2.5))
, выражен через его проекции (уравнение (2.5))
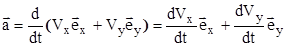 (3.3)
(3.3)
Выразим вектор  через проекции
через проекции  ,
, 
 (3.4)
(3.4)
Из (3.3) и (3.4) находим:
ах = 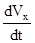 , т.к.
, т.к.
аналогично для  :
: 
Из (3.2) получим:  .
.
Малый участок криволинейной траектории всегда можно представить как дугу окружности радиуса R (рис. 3.2). Этот радиус называется радиусом кривизны траектории для данной точки кривой. Центр окружности (точка О) называется центром кривизны траектории. Из сказанного выше следует, что вектор  всегда направлен в сторону центра кривизны. Разложим вектор
всегда направлен в сторону центра кривизны. Разложим вектор 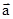 на две составляющие : одна из них
на две составляющие : одна из них  направлена по радиусу кривизны, вторая
направлена по радиусу кривизны, вторая  - по касательной (т.е. по линии перпендикулярной к радиусу кривизны).
- по касательной (т.е. по линии перпендикулярной к радиусу кривизны).
 (3.5)
(3.5)
Составляющая  называется нормальным (или центростремительным) ускорением и характеризует быстроту изменения направления вектора скорости.
называется нормальным (или центростремительным) ускорением и характеризует быстроту изменения направления вектора скорости.

|
 (3.6)
(3.6)
Составляющая  называется тангенциальным (или касательным) ускорением и характеризует быстроту изменения вектора скорости по величине. Следовательно, модуль вектора
называется тангенциальным (или касательным) ускорением и характеризует быстроту изменения вектора скорости по величине. Следовательно, модуль вектора  должен быть равен:
должен быть равен:
 (3.7)
(3.7)
Так как 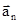 перпендикулярна
перпендикулярна  , то:
, то:
 (3.8)
(3.8)
Примеры.
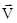
|
1. Прямолинейное движение: радиус кривизны R® ¥ (направление ñêîðîñòè не меняется). Из (3.6) получим :

2. Криволинейное движение с постоянной по величине скоростью V = const :
|

3. Равнопеременное движение: 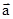 = const =>
= const =>  .
.
Из (3.4) получим (после интегрирования левой и правой части)

 (3.10)
(3.10)
Из(2.6) следует :
 (3.11)
(3.11)



 
h
|
Аналогично для оси y: Vy = V0y + ayt
 (3.12)
(3.12)
Например: тело брошено под углом a к горизонту вверх со скоростью  с высоты h ( рис.3.3).
с высоты h ( рис.3.3).




– Конец работы –
Эта тема принадлежит разделу:
Ускорение. Нормальное и тангенциальное ускорение
На сайте allrefs.net читайте: Ускорение. Нормальное и тангенциальное ускорение.
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Ускорение. Нормальное и тангенциальное ускорение.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?











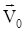



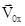





Новости и инфо для студентов