рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Вращательное движение. Угловая скорость. Угловое ускорение. Период, частота. Связь между линейными и угловыми характеристиками.
Реферат Курсовая Конспект
Вращательное движение. Угловая скорость. Угловое ускорение. Период, частота. Связь между линейными и угловыми характеристиками.
Вращательное движение. Угловая скорость. Угловое ускорение. Период, частота. Связь между линейными и угловыми характеристиками. - раздел Механика, Ускорение. Нормальное и тангенциальное ускорение Движение Точки По Дуге Окружности Радиуса ...
Движение точки по дуге окружности радиуса R называется вращательным движением рис (4.1). Линия перпендикулярная плоскости вращения (плоскости в которой лежит траектория) и проходящая через центр окружности (точка О) называется осью вращения. Изменение положения точки при вращательном движении характеризуют углом поворота Dj радиуса кривизны траектории (измеряют в радианах).
|
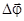 : вектор
: вектор 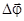 численно равен углу поворота Dj и направлен вдоль оси вращения согласно правилу правого винта. При вращении правого винта (буравчика) по направлению вращения, направление поступательного движения буравчика “показывает” направление вектора
численно равен углу поворота Dj и направлен вдоль оси вращения согласно правилу правого винта. При вращении правого винта (буравчика) по направлению вращения, направление поступательного движения буравчика “показывает” направление вектора 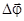
Угловая скорость вращения равна первой производной от угла поворота :
  
|
 (4.1).
(4.1).
Вектор 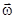 направлен так же, как и вектор
направлен так же, как и вектор  (т.е.
(т.е. 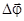 при Dt®0) (уравнение (4.1), рис. 4.1). Вращение с постоянной угловой скоростью называется равномерным. В этом случае:
при Dt®0) (уравнение (4.1), рис. 4.1). Вращение с постоянной угловой скоростью называется равномерным. В этом случае:
 (4.2),
(4.2),
где j - угол поворота за время t.
Равномерное вращательное движение характеризуют периодом вращения Т - это время одного оборота (т.е. время поворота радиуса вращения на угол 2p). Из (4.2) получим для равномерного вращательного движения (взяв t = T и, соответственно, j = 2p)
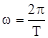 (4.3)
(4.3)
Число оборотов в единицу времени n равно:
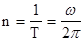 (4.4)
(4.4)
(Понятие периода Т и числа оборотов n можно использовать и для неравномерного вращательного движения, принимая за эти величины те значения, которые имела бы точка, если бы она вращалась равномерно с данным значением мгновенной скорости). Из (4.1) , (4.2) и определений Т и n следует:

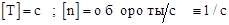
Вектор 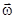 может меняться как вследствие изменения скорости вращения вокруг оси (т.е. изменяется величина w), так и вследствие поворота оси вращения (т.е. меняется направление вектора
может меняться как вследствие изменения скорости вращения вокруг оси (т.е. изменяется величина w), так и вследствие поворота оси вращения (т.е. меняется направление вектора 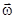 ). Пусть за время Dt вектор
). Пусть за время Dt вектор 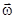 изменился на D
изменился на D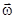 . Угловое ускорение
. Угловое ускорение  равно:
равно:
 (4.5)
(4.5)
Угловое ускорение есть первая производная от угловой скорости или вторая производная от угла поворота по времени Если ось вращения не меняет своего направления, то изменения 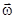 зависит только от изменения его величины Следовательно, для неизменного направления оси вращения из (4.5) получим :
зависит только от изменения его величины Следовательно, для неизменного направления оси вращения из (4.5) получим :
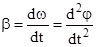 (4.6)
(4.6)
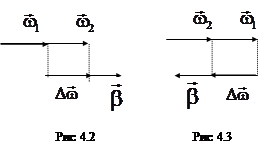
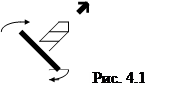
В этом случае, при увеличении величины w вектор D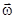 совпадает с вектором
совпадает с вектором 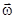 (рис 4.2), при уменьшении – противоположен (рис. 4.3).
(рис 4.2), при уменьшении – противоположен (рис. 4.3).
 |
Из сказанного и уравнения (4.5) следует: направление вектора  совпадает с направлением вектора
совпадает с направлением вектора 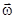 при ускоренном вращении, и противоположно направлению
при ускоренном вращении, и противоположно направлению 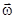 при замедленном.
при замедленном.
|
Из (4.6) получим: 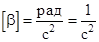 .
.
Найдем связь линейных характеристик движения (V, a,  ,
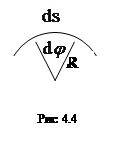
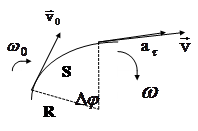
,  ) с угловыми (w, b). Из рис.4.4 видно:
) с угловыми (w, b). Из рис.4.4 видно:
d S = d jR 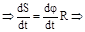
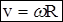 . (4.7)
. (4.7)
Учитывая правило векторного произведения можно записать (рис.4.4а):

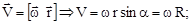
вектор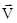 перпендикулярен
перпендикулярен 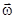 и
и 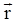 т.е. перпендикулярен
т.е. перпендикулярен 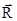 ).
).
Т.к.  то, учитывая (4.7), получим:
то, учитывая (4.7), получим: 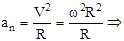

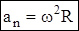 (4.8)
(4.8)
Если ось вращения не меняет своего положения в пространстве, то (с учетом (4.7)): 
Если при этом R = const , то получим : 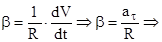
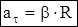 . (4.9)
. (4.9)
Из (3.8) , (4.8) и (4.9) находим:
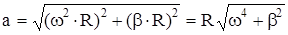
Пример: равноускоренное вращательное движение по окружности радиуса R: 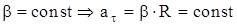
Из (4.6): 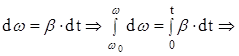
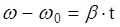 ;
; 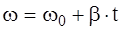 (4.10), (см. 3.10).
(4.10), (см. 3.10).
Из (4.1): 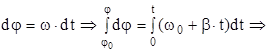
|
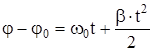 (4.11.), (см. 3.11 и 3.12).
(4.11.), (см. 3.11 и 3.12).
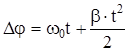 (4.11а).
(4.11а).
Т.к. 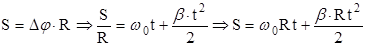 ,
,
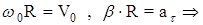
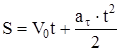 (4.12), (см. 3.11 и 3.12).
(4.12), (см. 3.11 и 3.12).

– Конец работы –
Эта тема принадлежит разделу:
Ускорение. Нормальное и тангенциальное ускорение
На сайте allrefs.net читайте: Ускорение. Нормальное и тангенциальное ускорение.
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Вращательное движение. Угловая скорость. Угловое ускорение. Период, частота. Связь между линейными и угловыми характеристиками.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?


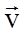


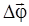
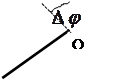





Новости и инфо для студентов