рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Моменты инерции некоторых однородных () тел.
Реферат Курсовая Конспект
Моменты инерции некоторых однородных () тел.
Моменты инерции некоторых однородных () тел. - раздел Механика, Радиус-вектор, скорость, ускорение 1) Момент Инерции Обруча Или Тонкостенного Цилиндра Относительно Оси, Проходя...
1) Момент инерции обруча или тонкостенного цилиндра относительно оси, проходящей через центр инертности перпендикулярно плоскости обруча.

|


|
2) Момент инерции диска или цилиндра относительно оси симметрии тела.

| Выберем внутри цилиндра тонкостенный цилиндр с 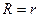 и толщиной и толщиной 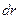 . .
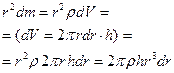
|


Учитывая, что 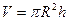 , получим
, получим 
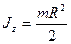 .
.
3) Момент инерции плоского стержня относительно оси, проходящей через центр тела и перпендикулярно к нему
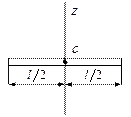
| 
|
4) Момент инерции шара относительно оси, проходящей через его центр.

| 
|

§13. Теорема Штейнера о моменте инерции относительно произвольной оси
Во всех четырех случаях мы рассматривали моменты инерции тела относительно оси, проходящей через центр инерции этих тел. С помощью теоремы Штейнера можно найти моменты инерции тел относительно других произвольных осей, что бывает необходимо, ибо вращение не всегда бывает относительно центра инерции.
Теорема Штейнера:
Момент инерции тела относительно произвольной оси равен сумме его момента инерции относительно оси, проходящей через центр масс и параллельно данной, и произведения массы тела на квадрат расстояния между осями
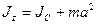
( - расстояние между осями z и c).
- расстояние между осями z и c).
Доказательство:
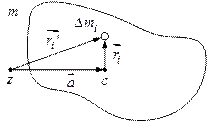
| Рассмотрим произвольное тело массой  . Пусть оси z и с перпендикулярны плоскости чертежа, а ось с проходит через центр инерции этого тела. Разобьем тело на элементарные участки с массами . Пусть оси z и с перпендикулярны плоскости чертежа, а ось с проходит через центр инерции этого тела. Разобьем тело на элементарные участки с массами 
|
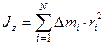 (по определению)
(по определению)

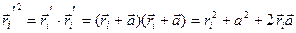
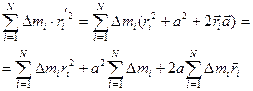
Видно, что  (по определению)
(по определению)

 (т.к.
(т.к.  )
)
Таким образом, 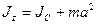
§14. Основное уравнение динамики вращательного движения
Пусть к твердому телу с неподвижной осью вращения в некоторой точке 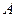 приложена сила
приложена сила 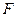 .
.

| Тогда если точка А совершает элементарное перемещение  , то элементарная работа силы , то элементарная работа силы 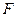 равна равна
 Представим силу
Представим силу 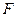 в виде суммы двух сил, одна из которых параллельна оси вращения z ( в виде суммы двух сил, одна из которых параллельна оси вращения z (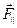 ), а другая перпендикулярна оси z ( ), а другая перпендикулярна оси z ( ). ).
|
Тогда элементарная работа  .
.
Точка 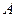 , как и все точки тела, движется по окружности, плоскость которой перпендикулярна оси z, а значит
, как и все точки тела, движется по окружности, плоскость которой перпендикулярна оси z, а значит  соединяет две точки этой окружности и также лежит в плоскости, перпендикулярной оси z, а значит и вектору
соединяет две точки этой окружности и также лежит в плоскости, перпендикулярной оси z, а значит и вектору 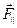 , т.е.
, т.е.  . Следовательно,
. Следовательно,  ,
,
где 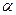 - угол между векторами
- угол между векторами  и
и  .
.
Рассмотрим вид сверху.

| В силу того, что 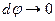 : :
 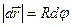 .
Вектор .
Вектор 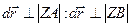 в силу малости в силу малости  . .
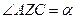 , как углы с взаимно перпендикулярными лучами. , как углы с взаимно перпендикулярными лучами.
|
 ,
,
где  .
.
Опр.
Величина  , равная расстоянию от линии, вдоль которой действует сила, до оси вращения, называется плечом силы.
, равная расстоянию от линии, вдоль которой действует сила, до оси вращения, называется плечом силы.
Опр.
Величина произведения проекции силы на плоскость вращения ( ) и плеча силы
) и плеча силы  называется моментом силы относительно оси вращения z.
называется моментом силы относительно оси вращения z.

Если сила 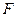 , приложенная к телу, приводит к увеличению угла поворота (т.е. к вращению тела по выбранному положительному направлению вращения), то момент такой силы является величиной положительной. Если же сила приводит к уменьшению угла, то момент силы отрицателен. Исходя из того, что величина элементарной работы равна
, приложенная к телу, приводит к увеличению угла поворота (т.е. к вращению тела по выбранному положительному направлению вращения), то момент такой силы является величиной положительной. Если же сила приводит к уменьшению угла, то момент силы отрицателен. Исходя из того, что величина элементарной работы равна  , то, согласно теореме о кинетической энергии (
, то, согласно теореме о кинетической энергии (
 ), приравнивая правые части уравнений получим:
), приравнивая правые части уравнений получим:
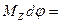

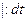


(Т.к.  и
и 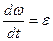 )
) 
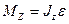
Это и есть основной закон динамики вращательного движения.
Формулировка закона:
Момент силы относительно оси вращения равен произведению момента инерции относительно этой оси и углового ускорения.
Легко можно показать, что если на тело, закрепленное вокруг оси вращения, действует множество сил с различными моментами, то алгебраическая сумма моментов сил относительно оси вращения равна произведению момента инерции относительно этой оси и углового ускорения:
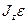
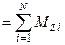
§15. Момент импульса.
Закон сохранения момента импульса
| Поступательное движение | Вращательное движение |
| m | 
|

| 
|
| a | 
|

| 
|

| 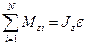
|
| Продолжая аналогию можно предположить, что | |
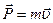
| 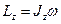
|
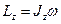 -момент импульса вращающегося вокруг оси z тела.
-момент импульса вращающегося вокруг оси z тела.
Продолжим аналогию еще далее, поставив вопрос, а обладает ли момент импульса свойством сохранения.
Действительно 

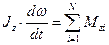 =>
=>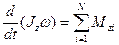 =>
=>  , Видно, если
, Видно, если 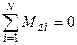 , то
, то 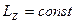
Таким образом, если алгебраическая сума моментов всех сил, приложенных к телу, относительно оси вращения равна 0, то момент импульса относительно этой оси есть величина постоянная.
Легко доказать, что таким же образом сохраняется момент импульса системы тел, вращающихся вокруг данной оси с различными угловыми скоростями  , а не одного только твердого тела.
, а не одного только твердого тела.
Закон сохранения момента импульса:
Момент импульса замкнутой системы тел относительно произвольной оси есть величина постоянная.
В заключении рассмотрим частные случаи в решении задач при определении момента импульса тела, размерами которого, по сравнению с расстоянием до оси вращения, можно пренебречь.
1. Материальная точка вращается по окружности.

2. Если точечное тело движется в произвольном направлении относительно оси вращения.

| 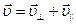
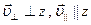
 ,
где ,
где  - расстояние от линии, направленной вдоль скорости тела до оси. - расстояние от линии, направленной вдоль скорости тела до оси.
|
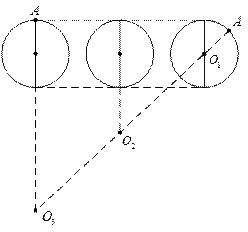
§16. Плоское движение. Энергия плоского движения
Опр.
Плоским движением называется такое движение, при котором все точки тела движутся в параллельных плоскостях.
Пример плоского движения: качение цилиндра (шара, диска) по горизонтальной и наклонной плоскостям.

| 
|
Любое плоское движение всегда можно представить как совокупность поступательного и вращательного движения. Причем разбиение такого движения можно осуществить бесконечным количеством способов, как поступательное движение некоторой оси О и вращения вокруг нее с угловой скоростью  . При этом при любом разбиении угловая скорость
. При этом при любом разбиении угловая скорость  будет одна и та же. И скорость любой точки можно представить как сумму поступательного и вращательного движения
будет одна и та же. И скорость любой точки можно представить как сумму поступательного и вращательного движения
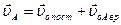 , где
, где 
Наглядный пример – качение цилиндра.
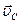 - скорость центра инерции
- скорость центра инерции

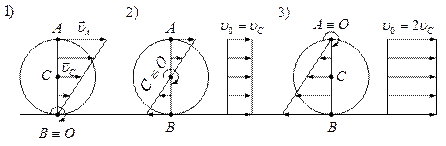
 Т. А движется с двойной скоростью центра инерции. Т. А движется с двойной скоростью центра инерции.
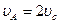
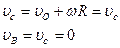
| 
|  (?)
(?)
|
Итак, скорость произвольной т.А при плоском движении есть  . Продифференцировав скорость по времени, получим
. Продифференцировав скорость по времени, получим  , где
, где 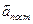 – ускорение оси О и
– ускорение оси О и  -ускорение при вращательном движении вокруг оси О и (
-ускорение при вращательном движении вокруг оси О и ( )
)
 ;
;  .
.
При плоском движении всегда можно найти такую ось, скорость движения точек на которой равна нулю. И таким образом рассматривать движение всего тела как вращение вокруг мгновенной оси вращения (у цилиндра – это точка касания поверхности).
Наиболее удобным является разбиение плоского движения на поступательное, происходящее со скоростью центра инерции, и вращение вокруг оси, проходящей через центр инерции.
В этом случае скорость произвольной точки твёрдого тела А имеет вид:
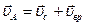 ; где
; где 
 ; где
; где  при этом
при этом  ,
, 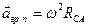 .
.
Можно показать, что кинетическая энергия при плоском движении равна сумме половины произведения массы тела на квадрат скорости его центра инерции и кинетической энергии вращения тела вокруг центра инерции:
 , где
, где  .
.
Пример: Чему равна кинетическая энергия движения цилиндра массой 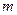 , катящегося по горизонтальной плоскости со скоростью
, катящегося по горизонтальной плоскости со скоростью 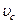 .
.
 ;
;
 =>
=> 
Тема 4. Механические колебания
Опр.
Колебаниями называется движение тела положения равновесия.
Опр.
Колебания, при которых все физические параметры изменяются по закону синуса или косинуса, называются гармоническими.
§17. Свободные незатухающие колебания
1) Колебания груза на пружине.
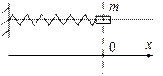
| Система, состоящая из горизонтально расположен-ного штыря, на который под действием пружины |
жесткости k перемещается без трения груз массой m.
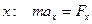 ,
, 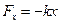 - закон Гука.
- закон Гука.

Получим  =>
=> 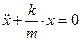
 – положительное число
– положительное число 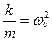 =>
=> 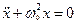 .
.
Это и есть дифференциальное уравнение, решением которого является гармонические функции. Уравнение содержит неизвестную функцию 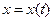 и её вторую производную по времени
и её вторую производную по времени 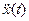 .
.
Опр.
Уравнения, содержащие производные функций называются дифференциальными.
Способы их решения мы будем изучать в теории дифференциальных уравнений. Сейчас важно знать, что это дифференциальное уравнение второго порядка, линейное, с постоянными коэффициентами. Его решение имеет вид:
 , где
, где  ,
, 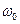 ,
, 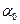 – суть некоторой константы.
– суть некоторой константы.
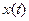 – смещение тела от положения равновесия;
– смещение тела от положения равновесия;  – амплитуда колебаний;
– амплитуда колебаний; 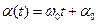 – фаза гармонического колебания;
– фаза гармонического колебания; 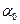 – начальная фаза (
– начальная фаза ( ).
).
Опр.
Время одного полного колебания – период колебания. (Т)
 – число колебаний в единицу времени.
– число колебаний в единицу времени.
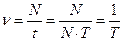 – частота колебания
– частота колебания
[ ]=c-1=Гц; [
]=c-1=Гц; [ ]=c; [
]=c; [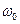 ]=рад/с
]=рад/с
Как известно, период колебаний синуса и косинуса =>
=>  =>
=> 
 – период колебаний груза на пружине.
– период колебаний груза на пружине.

 – амплитуда скорости.
– амплитуда скорости.

 – амплитуда ускорения.
– амплитуда ускорения.
2) Малые колебания физического и математического маятников.
Опр.
Под физическим маятником понимают твёрдое тело, которое способно колебаться вокруг горизонтальной оси, не проходящей через центр масс.

| Положение физического маятника будем характеризовать углом поворота 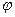 , отсчитываемым против часовой стрелки по вертикали до отрезка, соединяющего ось z с центром инерции , отсчитываемым против часовой стрелки по вертикали до отрезка, соединяющего ось z с центром инерции  . Длина его . Длина его  . Если угол . Если угол 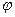 невелик, то момент силы тяжести относительно оси z
Равен невелик, то момент силы тяжести относительно оси z
Равен ( ( , так как он приводит к уменьшению угла поворота). , так как он приводит к уменьшению угла поворота).
|
Момент силы 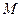 относительно оси z равен нулю.
относительно оси z равен нулю.
Согласно основному уравнению динамики вращательного движения:
 =>
=>
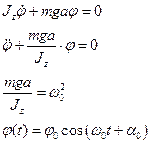

Частным случаем физического маятника является математический маятник, под которым понимают тело в виде материальной точки, подвешенное на невесомой нерастяжимой нити.
В этом случае  ,
,  .
.
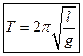 – период колебаний математического маятника.
– период колебаний математического маятника.
§18. Свободные затухающие колебания
Обратимся вновь к колебательной системе груза на пружине.
В действительности свободные колебания всегда со временем затухают, если нет подпитки энергией из-за сил трения или сопротивления в системе.
Сила сопротивления или трения обычно пропорциональна скорости и направлена против движения.
 , где
, где  – коэффициент трения.
– коэффициент трения.
Тогда по второму закону Ньютона для груза на пружине мы запишем с учётом силы трения:
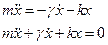
Поделив на m и обозначив  , получим:
, получим:
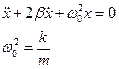
Решение этого дифференциального линейного уравнения второго порядка с постоянными коэффициентами имеет вид  , где
, где  – циклическая частота,
– циклическая частота,  – некая константа, начальная амплитуда.
– некая константа, начальная амплитуда.
Анализируя данное решение отметим, что частота затухающих колебаний меньше, а период – больше, соответственно частоты и периода незатухающих колебаний. Это понятно, так как сила трения тормозит движение груза.
По аналогии с незатухающими колебаниями величину, стоящую перед косинусом называют амплитудой затухающих колебаний, которая экспоненциально убывает со временем:  .
.

Для характеристики быстроты убывания амплитуды вводят понятие декремента затухания колебаний, который показывает во сколько раз уменьшается амплитуда колебаний за один период:
 .
.
Логарифм 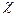 принято называть логарифмическим декрементом затухания.
принято называть логарифмическим декрементом затухания.

Физический смысл величины  – число колебаний, во время которых амплитуда убывает в е раз.
– число колебаний, во время которых амплитуда убывает в е раз.
Используя понятие  , амплитуду колебаний можно представить в виде:
, амплитуду колебаний можно представить в виде:
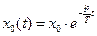 .
.
§19. Вынужденные колебания. Резонанс
Вновь возвращаемся к системе колебания груза на пружине, но теперь на груз, кроме пружины и силы трения действует ещё и внешняя горизонтальная периодическая сила.
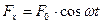
 – амплитуда периодической внешней силы;
– амплитуда периодической внешней силы;  – её частота.
– её частота.
В этом случае второй закон Ньютона запишется
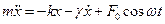
Поделим левую и правую части на m (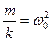 ;
;  ):
):
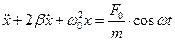 - дифференциальное уравнение.
- дифференциальное уравнение.
Решением этого уравнения является функция 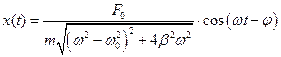 ,
,
где  .
.
Величина, стоящая перед косинусом, называется амплитудой вынужденных колебаний. Она зависит от частот внешней силы.
 , где
, где 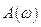 – амплитуда,
– амплитуда,  .
.
Задача: Определить, при какой частоте внешних колебаний их амплитуда будет максимальной.
 =>
=> 
Опр.
Возрастание амплитуды вынужденных колебаний при приближении частоты внешней силы к некоторой частоте, именуемой резонансной, принято называть резонансом.

| 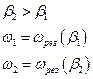
|
С увеличением трения в системе, (то есть с ростом  ) резонанс менее выражен. С увеличением
) резонанс менее выражен. С увеличением  резонанс смещается в сторону меньших частот. При
резонанс смещается в сторону меньших частот. При 
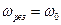 , а
, а 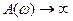 .
.
§20. Сложение колебаний
Вопрос о сложении механических колебаний возникает, как правило, при наложении волн, распространяющихся в упругих средах. В этом случае частицы среды участвуют в нескольких независимых друг от друга колебаниях. С различными в общем случае направлениями, амплитудами, частотами и начальными фазами.
Мы рассмотрим лишь несколько частных случае сложения колебаний.
1) Сложение колебаний одного направления одинаковых частот.
Пусть точка одновременно участвует в двух колебаниях относительно оси Ox, описываемых законом:

Тогда результирующие движение точки будет описываться законом:

Всегда можно найти такие  и
и 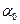 , что
, что
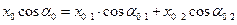 (1)
(1)
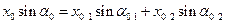 (2)
(2)
Действительно, если мы поделим (2) на (1), получим
 .
.
Возведя (1) и (2) в квадрат и сложив левые и правые части этих уравнений, получим:
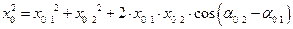
С учётом этого

Таким образом результирующее движение точки представляет собой гармоническое колебание той же частоты с амплитудой, имеющей максимальное значение при отсутствии разности начальных фаз и минимальное при разности начальных фаз 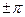 (противофаза).
(противофаза).
2) Биения.
Если частоты колебаний одного направления не одинаковы, то результирующее движение точки не будет гармоническим колебанием, это будет более сложный колебательный процесс.
Особый интерес здесь представляет случай, когда колебания мало отличаются по частоте. В этом случае результирующее колебание можно рассмотреть как гармоническое с пульсирующей амплитудой. Такой колебательный процесс принято именовать биениями.
Пусть точка одновременно участвует в двух колебаниях вдоль оси Ox для простоты с равными амплитудами и нулевыми начальными фазами. Частоты колебаний равны:  и
и 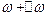 , где
, где 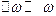

Тогда результирующее колебание будет описываться законом

Множитель, заключенный в скобках изменяется по гармоническому закону значительно медленнее, чем второй, поэтому его можно рассматривать как зависящую от времени по гармоническому закону амплитуду.

Из графика видно, что модуль величины в скобках можно рассматривать как амплитуду
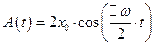
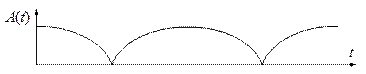
Период пульсирующей амплитуды в 2 раза меньше периода функции  , поэтому частота пульсации, именуемая частотой биений, равна разности частот складываемых колебаний.
, поэтому частота пульсации, именуемая частотой биений, равна разности частот складываемых колебаний.
3) Сложение взаимно перпендикулярных колебаний одинаковых частот.
Пусть точка участвует в двух взаимно перпендикулярных колебаниях, описываемых законами:
а) 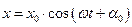

Тогда  =>
=> 
.
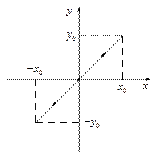
| Т.е. точка движется вдоль прямой с коэффициентом наклона 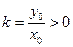
|
б) если разность начальных фаз: 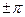 .
.
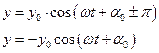
 .
.
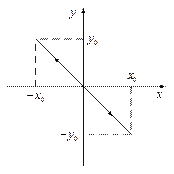
| Т.е. точка движется вдоль прямой с коэффициентом наклона  . .
|
В) если разность начальных фаз:  .
.

Тогда
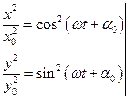 =>
=>  – уравнение эллипса.
– уравнение эллипса.

|
Точка движется по эллипсу по часовой стрелке при разности фаз  и против часовой стрелке при и против часовой стрелке при  . .
|
Если  , тогда эллипс превращается в окружность:
, тогда эллипс превращается в окружность: 
Отметим, что если разность начальных фаз складываемых взаимно перпендикулярных колебаний отлична от 0, 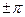 ,
,  , то можно показать, что в этом случае точка будет двигаться по эллипсу (если
, то можно показать, что в этом случае точка будет двигаться по эллипсу (если  , то по окружности), но полуоси эллипса не будут совпадать с осями Ox и Oy.
, то по окружности), но полуоси эллипса не будут совпадать с осями Ox и Oy.
II Молекулярная физика. Термодинамика
§21. Термодинамика и молекулярно-кинетическая теория в изучении тепловых явлений. Основные макроскопические параметры газообразных тел
Опр.
Тепловые явления – физические процессы в природе, связанные с нагревом и охлаждением тел, а также структурными полиморфными превращениями: сублимация, плавление, испарение, кристаллизация и другие физическими превращениями.
Исторически сложилось 2 подхода к таким тепловым явлениям: ТД – термодинамика и МКТ – молекулярно-кинетическая теория, МКТ ещё именуют молекулярной физикой. ТД и МКТ изучают одни и те же тепловые явления.
ТД более древняя наука с идеально разработанной теорией. ТД изучает тепловые явления, не обращаясь к микроструктуре тел, на основе эмпирических законов и термодинамических начал.
МКТ изучает макроскопические свойства тел на основе представлений о движении и взаимодействии микрочастиц (молекул и атомов). МКТ – новая наука, появляется в конце 19-начале 20в. Её развитие позволило обосновать законы ТД на основе механических представлений поведения атомов и молекул и воздать новую научную дисциплину – статическая физика, которая основана на математических методах теории вероятности, т.к. пытается выявить закономерности теплового движения огромного числа микрочастиц.
Мы не будем раздельно рассматривать 2 этих подхода, но в их совокупности и взаимосвязи при изучении тепловых явлений.
В начале нашего изучения – газовые законы, которые выводятся из МКТ, а в ТД являются эмпирическими законами.
Количество вещества в МКТ неудобно измерять количеством молекул, т.к. это очень большое число, поэтому его измеряют в молях.
Опр.
Молем называется такое количество вещества, масса которого, выраженная в граммах, численно равна массе молекулы этого вещества, выраженного в а.е.м.
Массу одного моля вещества называют молярной массой.
 = кг/моль
= кг/моль
 ;
; 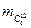 - масса атома
- масса атома 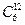 .
.
Если 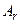 - атомная масса вещества, выраженная в а.е.м. (
- атомная масса вещества, выраженная в а.е.м. ( ), то его молекулярная масса по определению равна
), то его молекулярная масса по определению равна  г/моль, тогда число молекул в моле любого вещества равно:
г/моль, тогда число молекул в моле любого вещества равно:
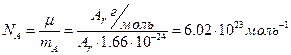 - число Авогадро.
- число Авогадро.
А значит, молярная масса есть масса числа Авогадро молекул.
Число молей есть 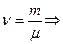 число молекул
число молекул 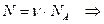

– Конец работы –
Эта тема принадлежит разделу:
Радиус-вектор, скорость, ускорение
Механика наука изучающая перемещение в пространстве твердых тел и равновесие их под воздействием сил... Кинематика раздел механики изучающий движение твердых тел не интересуясь... Тела которые при движении не деформируются твердые тела...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Моменты инерции некоторых однородных () тел.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов