рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Механика
- /
- Радиус-вектор, скорость, ускорение
Реферат Курсовая Конспект
Радиус-вектор, скорость, ускорение
Радиус-вектор, скорость, ускорение - раздел Механика, I Механика Механика – Наука, Изучающая Перемещение В Пространстве Тв...
I Механика
Механика – наука, изучающая перемещение в пространстве твердых тел и равновесие их под воздействием сил.
Кинематика – раздел механики, изучающий движение твердых тел, не интересуясь причинами, обусловливающих это движение.
Тела, которые при движении не деформируются – твердые тела.
§1 Основные кинематические характеристики движения материальной точки
(радиус-вектор, скорость, ускорение)
Механическое движение твердого тела сводится к двум видам: поступательному и вращательному.
Опр.
Поступательное движение – движение, при котором любая прямая, связанная с этим телом, перемещается параллельно самой себе.
Опр.
Вращательное движение – движение твердого тела, при котором все точки данного тела движутся по окружности, при этом центры окружностей лежат на одной прямой. При этом любое механическое движение можно разбить на поступательное и вращательное.
Опр.
Материальная точка – тело, размерами которого можно пренебречь в условиях данной задачи.
Учитывая, что при поступательном движении твердого тела конечных размеров, все его точки движутся совершенно одинаково (у них одинаковые, но смещенные друг относительно друга траектории, скорость и ускорения в любой момент времени), то кинематика поступательного движения твердого тела сводится к кинематике материальной точки.
Для описания движения необходимо выбрать систему отсчета.
Опр.
Система отсчета – совокупность тела отсчета, системы координат, способа измерения времени.
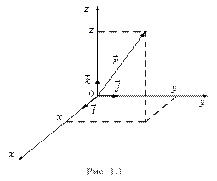
| Положение материальной точки в системе отсчета принято задавать радиус-вектором, начало которого совпадает с началом координат, а конец с самой точкой. Проекция радиус-вектора на оси совпадает с координатами материальной точки (x,y,z) |
Если по осям направить единичные вектора  , то радиус-вектор можно представить в виде суммы трех взаимно перпендикулярных векторов.
, то радиус-вектор можно представить в виде суммы трех взаимно перпендикулярных векторов.

Или, как говорят, разложить вектор по базису ортогональных векторов. Длина, или модуль: 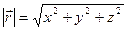


|
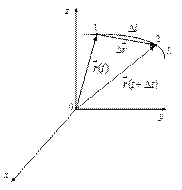
Пусть материальная точка перемещается вдоль кривой линии L, называемой траек-торией. При этом в момент времени t материальная точка находилась в положении 1, с радиус-вектором 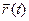 , а спустя время , а спустя время 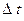 в положении 2 в положении 2
|
с радиус-вектором 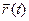 , а спустя время
, а спустя время 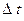 в положении 2 с радиус-вектором
в положении 2 с радиус-вектором  . Длина траектории
. Длина траектории  , заключенная между двумя точками 1 и 2 – длина пути материальной точки за время
, заключенная между двумя точками 1 и 2 – длина пути материальной точки за время 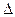 t.
t. 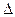 r, направленный из 1 в 2, есть вектор перемещения материальной точки за время
r, направленный из 1 в 2, есть вектор перемещения материальной точки за время 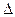 t:
t:
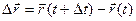
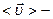 среднее значение скорости материальной точки на участке траектории 1-2 или за время
среднее значение скорости материальной точки на участке траектории 1-2 или за время 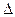 t, равное отношению
t, равное отношению 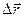 ко времени
ко времени  , за которое произошло это перемещение.
, за которое произошло это перемещение.

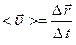
 Вектор
Вектор  направлен по
направлен по 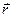 .
.
 Вектор
Вектор 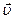 , равный
, равный 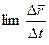 , за которое это перемещение произошло, при стремлении
, за которое это перемещение произошло, при стремлении  к 0, называется мгновенной скоростью материальной точки в положении 1 или момент времени t:
к 0, называется мгновенной скоростью материальной точки в положении 1 или момент времени t:

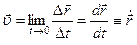 ,
,
 т.е вектор скорости
т.е вектор скорости 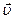 равен производной от радиус-вектора
равен производной от радиус-вектора 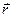 по времени.
по времени.

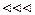
Отметим, что при уменьшении времени  точка 2 приближается к точке 1, и угол между вектором
точка 2 приближается к точке 1, и угол между вектором 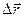 и касательной к траектории в точке 1уменьшается и в пределе стремится к 0. Таким образом, в точке 1 и в любой другой точке траектории вектор
и касательной к траектории в точке 1уменьшается и в пределе стремится к 0. Таким образом, в точке 1 и в любой другой точке траектории вектор 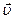 направлен всегда по касательной к траектории (или всегда направлен по направлению движения)
направлен всегда по касательной к траектории (или всегда направлен по направлению движения)
Найдем связь между проекциями векторов  и
и 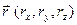 . С одной стороны, согласно определению,
. С одной стороны, согласно определению,

 .
.
С другой стороны вектор  можно разложить по базису
можно разложить по базису 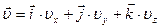 . Сравнивая эти выражения для
. Сравнивая эти выражения для  получаем, что
получаем, что  ,
, 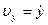 .
.  . При этом модуль скорости, согласно теореме Пифагора, равен
. При этом модуль скорости, согласно теореме Пифагора, равен

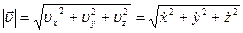
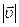 можно найти, используя понятие длины пути, проходимого материальной тоской.
можно найти, используя понятие длины пути, проходимого материальной тоской.
Т.к. предел отношения модуля вектора перемещения к длине пути при стремлении 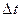 к нулю равен 1, то модуль скорости равняется
к нулю равен 1, то модуль скорости равняется  , т.е. модуль вектора скорости равен производной от пути, проходимого материальной точкой, по времени.
, т.е. модуль вектора скорости равен производной от пути, проходимого материальной точкой, по времени.
|
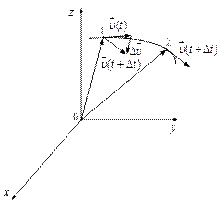
С течением времени при движении материальной точки по траектории вектор скорости в общем случае изменяется как по величине, так и по направлению. Пусть в точке 1 траектории в момент времени t вектор скорости равен  , а в точке 2 в момент времени , а в точке 2 в момент времени
|
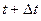 равен
равен  . Тогда вектор приращения скорости за время
. Тогда вектор приращения скорости за время 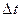 равен
равен 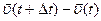 .
.
Вектор  , равный отношению вектора приращения скорости ко времени
, равный отношению вектора приращения скорости ко времени 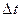 , за которое происходит это приращение, называется средним ускорением материальной точки на участке траектории 1-2 (или за время
, за которое происходит это приращение, называется средним ускорением материальной точки на участке траектории 1-2 (или за время 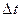 ).
).
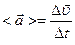


Вектор 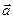 , равный пределу отношения вектора приращения скорости ко времени
, равный пределу отношения вектора приращения скорости ко времени 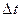 , за которое это приращение произошло, при стремлении
, за которое это приращение произошло, при стремлении 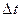 к 0, называется ускорением материальной точки в положении 1 (в момент времени t).
к 0, называется ускорением материальной точки в положении 1 (в момент времени t).
 ,
,
т.е. вектор ускорения равен производной от вектора скорости по времени.
Поскольку сам вектор скорости есть производная от радиус-вектора по времени, то ускорение есть производная второго порядка от радиус-вектора по времени
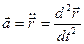 .
.

Найдем связь между проекциями радиус-вектора 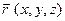 , вектора скорости
, вектора скорости  и вектора ускорения
и вектора ускорения 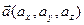 .
.
С одной стороны, согласно сказанному выше, вектор ускорения равен 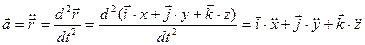 .
.
С другой стороны
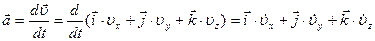
или  .
.
Сравнивая записанные для вектора ускорения выражения, находим, что
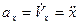

Модуль вектора 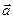 , согласно теореме Пифагора, равен
, согласно теореме Пифагора, равен
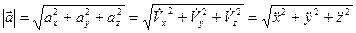
§2 Криволинейное движение материальной точки. Нормальная и тангенциальная составляющие ускорения при криволинейном движении
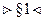
Направим вектор единичной длины 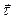 по направлению вектора скорости, тогда
по направлению вектора скорости, тогда  , а вектор ускорения
, а вектор ускорения
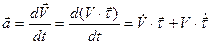 . (*)
. (*)
Выясним, каким образом направлен вектор производной 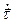 .
.

|
Обозначим через  поло-
жение вектора поло-
жение вектора 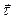 в момент времени t, а через в момент времени t, а через 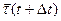 - в момент времени - в момент времени 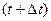 . По определению . По определению 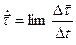 . .
|
При уменьшении 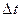 угол между векторами
угол между векторами 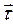 и
и 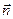 (
(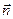 перпендикулярен вектору
перпендикулярен вектору 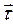 и направлен в сторону его поворота) уменьшается и в пределе стремится к 0. Таким образом, производная
и направлен в сторону его поворота) уменьшается и в пределе стремится к 0. Таким образом, производная 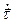 есть вектор, перпендикулярный вектору
есть вектор, перпендикулярный вектору 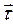 и направленный в сторону его поворота.
и направленный в сторону его поворота.
Обозначим через  длину вектора
длину вектора 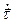 , получим
, получим  . Таким образом, выражение (*) запишется
. Таким образом, выражение (*) запишется  , т.е.
, т.е. 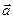 можно представить в виде суммы двух взаимно ортогональных векторов, один из которых
можно представить в виде суммы двух взаимно ортогональных векторов, один из которых  параллелен вектору скорости и называется вектором тангенциального ускорения, а другой
параллелен вектору скорости и называется вектором тангенциального ускорения, а другой 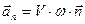 перпендикулярен вектору скорости и называется вектором нормального ускорения.
перпендикулярен вектору скорости и называется вектором нормального ускорения.
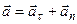

|
По теореме Пифагора 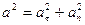  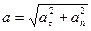 .
Т.к. вектор .
Т.к. вектор 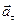 направлен параллельно вектору скорости, направлен параллельно вектору скорости,
|
то можно сказать, что он не изменяет направления вектора скорости, а изменяет лишь его модуль (абсолютную величину).
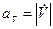
Т.к. вектор 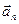 перпендикулярен вектору скорости, то можно сказать, что он не изменяет модуля вектора скорости, а изменяет лишь его направление. Модуль
перпендикулярен вектору скорости, то можно сказать, что он не изменяет модуля вектора скорости, а изменяет лишь его направление. Модуль 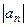 находим из теоремы Пифагора:
находим из теоремы Пифагора:
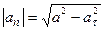
§3 Движение материальной точки по окружности. Связь угловых и линейных величин
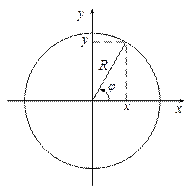
При вращении твердого тела вокруг неподвижной оси все его точки описывают окружности того или иного радиуса и в любой момент времени имеют равные угловые скорости и угловые ускорения. Поэтому кинематику твердого тела можно свести к кинематике движения материальной точки по окружности.
|
Положение материальной точки при движении по окружности можно однозначно охарактеризовать углом поворота 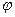 , который можно отсчитывать от положительной части оси ОХ против (по) часовой стрелки до радиуса R, проведенного от начала коор- , который можно отсчитывать от положительной части оси ОХ против (по) часовой стрелки до радиуса R, проведенного от начала коор-
|
динат к материальной точке (выбор направления отсчета 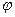 произволен).
произволен).
Угол, отсчитываемый в противоположном от выбранного направления, считается отрицательным.
 [рад] 1 рад =
[рад] 1 рад =  =57,3°.
=57,3°.
Положение материальной точки на окружности можно характеризовать числом оборотов N, которое может быть нецелым, тогда связь между N и 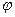 определяется
определяется
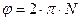 . (*)
. (*)
Производная от угла поворота материальной точки по времени называется угловой скоростью
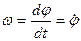
При равномерном вращении угловая скорость  численно равна углу поворота в единицу времени [рад/с].
численно равна углу поворота в единицу времени [рад/с].
Производная от числа оборотов N по времени есть частота вращения.
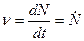
При равномерном вращении частота численно равна числу оборотов в единицу времени [Гц].
Продифференцировав правую и левую части уравнения (*), получим
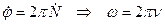
В общем случае  изменяется с течением времени.
изменяется с течением времени.
Производная угловой частоты по времени – угловое ускорение 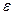 .
.
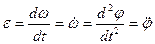
Определим связь линейных и угловых величин при вращательном движении, для чего отметим, что координаты материальной точки (x,y) связаны с 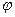 соотношениями
соотношениями
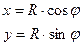
Дифференцируя их по времени, получим
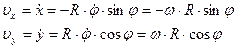 (**)
(**)
По теореме Пифагора найдем модуль вектора скорости 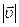 .
.

Поскольку мы находим модуль вектора скорости, нас интересует арифметическая величина корня, а 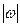 может быть меньше 0.
может быть меньше 0.
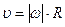
Учитывая, что 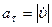 , продифференцировав его, получим
, продифференцировав его, получим 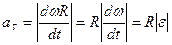 .
.

Продифференцировав проекции скорости (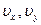 ) по времени с учетом (**), получим
) по времени с учетом (**), получим
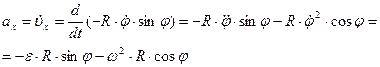
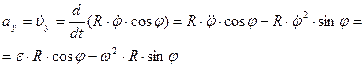
Тогда 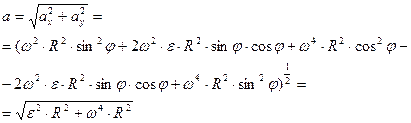
Модуль вектора 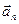 находим по формуле
находим по формуле 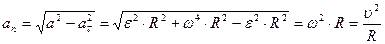

Замечание
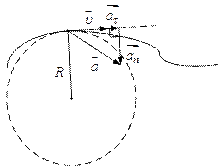
| В случае движения материальной точки вдоль произвольной плоской траектории, бесконечно малый участок 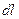 вблизи любой точки траектории можно рассматривать как дугу окружности, радиус которой R, называемый радиусом вблизи любой точки траектории можно рассматривать как дугу окружности, радиус которой R, называемый радиусом
|
кривизны траектории в рассматриваемой точке. Соотношение для величин 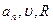 в этом случае остается таким же, как и в случае движения материальной точки по окружности радиуса R.
в этом случае остается таким же, как и в случае движения материальной точки по окружности радиуса R.
§4 Частные случаи движения материальной точки
1) 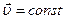
2) 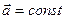
3) 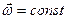
4) 
Движение с постоянной скоростью
Для выявления физического смысла положим в законе о движении - радиус-вектор,…Движение материальной точки с постоянным ускорением
, где - константа интегрирования. Физический смысл константы также определим при - скорость в начальный момент времени. Очевидно, что для координат…Движение материальной точки по окружности с постоянной угловой скоростью
Согласно определению угловой скорости
 . Проинтегрировав данное выражение, получим
. Проинтегрировав данное выражение, получим
 ,
,
где 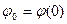 - начальное значение угла поворота.
- начальное значение угла поворота.
Движение материальной точки по окружности с постоянным угловым ускорением
где - начальная угловая скорость. Т.к. . Проинтегрировав данное выражение, получим ,Первый закон Ньютона
, если Найдем такие системы отсчета (или хотя бы одну, т.к. все остальные, движущиеся…Второй закон Ньютона
Если на тело действуют несколько сил, то вместо силы F следует подставить…Третий закон Ньютона
Третий закон Ньютона утверждает, что силы при взаимодействии двух тел всегда возникают парами. Они приложены к разным телам, при этом равны по величине и противоположны по направлению.
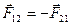
Закон всемирного тяготения
, где []Метафизический смысл
Закон сохранения импульса свидетельствует об однородности пространства (нет особых точек в пространстве, все точки равноправны). Закон сохранения… Импульс материальной точки есть произведение ее массы на скоростьТеорема о кинетической энергии
Эта теорема верна не только для поступательного движения твердого тела, но и в случае его произвольного движения. Кинетической энергией обладают только движущиеся тела, поэтому ее называют…Моменты инерции некоторых однородных () тел.
2) Момент инерции диска или цилиндра относительно оси симметрии тела. Выберем внутри цилиндра…Макроскопические параметры (P, V, T).
Тепловое движение молекул газа можно характеризовать кинетической энергией поступательного движения молекулы . Из опыта установлено, что при тепловом контакте выравнивается со временем, т.е. молекулы более нагретого газа теряют…Закон Дальтона.
Рассмотрим газовую смесь, состоящую из n-компонентов. Обозначим - количество молей i-той константы смеси,- число молей i-той константы. Давление, которое оказывал бы какой-либо из газов (констант) в отсутствии всех… Согласно определению парциальное давление i-той константы этого газа равно: .Работа газа
тогда конечное значение работы газа по изменению его объёма от до определяется суммой элементарных работ или интегралом . Согласно геометрическому смыслу интеграла модуль работы равен площади… Работа газа А не является функцией состояния в отличие от внутренней энергии , а зависит от формы кривой или от вида…Первое начало термодинамики.
Внутреннюю энергию тела можно изменять не только путём совершения работы… При отсутствии работы из закона сохранения энергии получаем, что , также как и , является функцией процесса при…Теплоёмкость идеального газа. Уравнение Майера.
Теплоёмкость газа при постоянном объёме называется изохорной теплоёмкостью и обозначается . В этом случае газ не совершает работу, а значит по первому закону термодинамики и .– Конец работы –
Используемые теги: Радиус-вектор, Скорость, Ускорение0.064
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Радиус-вектор, скорость, ускорение
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов