Кинематические пары

Механизмом называется система подвижно соединенных между собой твердых тел, предназначенных для преобразования незави­симых движений одного или нескольких из них в требуемые движения остальных тел. Твердые тела, из которых образованы механизмы, на­зываются звеньями, а соединение двух звеньев, допускающее их относительное движение, - кинематической парой. Каждое звено пред­ставляет собой одну деталь, выполненную без сборочных операций (рисунок 1.1, а), или кинематически неизменяемую сборочную единицу, состоящую из нескольких деталей (рисунок 1.1, б).

Звенья механизма, которым сообщаются независимые движения, называются ведущими. Ведомыми называются звенья, совершающие требуемые движения; на эти звенья действуют силы полезного со­противления, для преодоления которых механизм предназначен. Зве­но, относительно которого рассматривается движение остальных звеньев, называется стойкой. При исследовании механизмов на их схемах всем подвижным звеньям присваиваются порядковые номера: первый 1 - ведущему звену и последний п- ведомому. Стойку обычно нумеруют нулем, а для отличия от подвижных звеньев ее под­черкивают косыми штрихами. Кинематические пары обозначают ла­тинскими прописными буквами.

Поверхность, линия или точка, которыми данное звено сопри­касается с другим звеном, образуя кинематическую пару, называет­ся геометрическим элементом звена или просто элементом звена.

Пары с линейным или точечным контактом называются высшими (таблица 1.1, а, б, в, ж,), а с поверхностным - низшими (таблица 1.1, г, д, е, з, и, к ).

Форма элементов каждого звена пары и их взаимное рас­положение определяют основное свойство кинематических пар - вид относительного движения их звеньев. Для его определения одно звено пары обращают в стойку (делают неподвижным), а другому сообщают движения, допускаемые принятой формой

		Рисунок 1.1

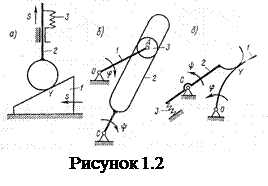
геометрических элементов. В низших парах относительное движение звеньев 1 и 2 (вращательное или поступательное) сопровождается скольжением геометрических элементов, а в высших - происходит чистое сколь­жение (рисунок 1.2, а), чистое качение (рисунок 1.2, б), скольжение и ка­чение одновременно (рисунок 1.2, в). Скольжение элементов звеньев высшей пары сопровождается износом (истиранием) и потерями мощ­ности на трение. Износ звеньев и потери будут уменьшены, если с помощью ролика 3 (рисунок 1.2, б) качение со скольжением или одно скольжение заменить чистым качением. Аналогично и в низших парах: для уменьшения износа и потерь трение скольжения часто за­меняют трением качения, вводя в зазор между элементами звеньев шарики (рисунок 1.3, а) или ролики (рисунок 1.3, б).

В этом случае низшие вращательные и поступательные пары скольжения обращаются в низшие вращательные и поступательные пары чистого качения.

При обращении одного звена пары в стойку можно определить также вид траекторий отдельных точек звена, оставшегося подвиж­ным. Если эти траектории являются плоскими кривыми, лежащими в параллельных плоскостях, то кинематическая пара является плоской (таблица 1.1, д,з,и). В пространственных парах траектория относительного движения точки подвиж­ного звена является про­странственной кривой (таблица1.1, а,б,в,г,е).

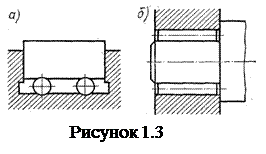Таблица 1.1

Класс пары	Разновидности пары	Число связей	Число степеней свободы
I     II     III     IV     V		--	--     --     --   --

Для того чтобы вид относительного движения звеньев пары соответствовал выбранным геометрическим элементам, последние должны на­ходиться в постоянном контакте или, иначе говоря, элементы звеньев пары должны быть замкнутыми. Замыкание в большинстве низших пар обеспечивается формой элементов и их контакт не может быть нарушен самопроизвольно (таблица 1.1, е,з,и,к). В высших парах постоянный контакт элементов звеньев осуществляется под действием силы тяжести подвижного звена (таблица 1.1, а,б,в,д,ж), силы упругости пружины 3 (рисунок 1.2, а,в) или приданием звеньям пары соответствующей формы (рисунок 1.2, б). В последнем случае замыкание называется геометрическим.

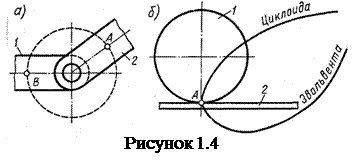
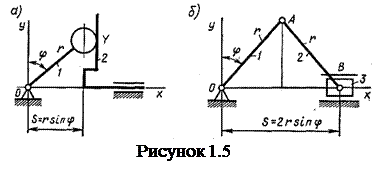
Существенным отличием высших пар от низших является их необ­ратимость. Если при обращении низшей пары (подвижного звена в неподвижное, а неподвижного в подвижное) вид траекторий контакти­рующих точек при относительном движении звеньев 1 и 2 остается неизменным (рисунок 1.4, а), то при обращении высших пар точки А₁ и A₂ описывают разные кривые (рисунок 1.4, б). Следовательно, низшие пары обеспечивают один и тот же характер относительного движе­ния независимо от того, какое звено пары обращено в стойку. Выс­шие пары позволяют получать самые разнообразные виды относи­тельного движения в зависимости от того, какие кривые выбраны в качестве профилей (кривых в сечении плоскостью вращения) звень­ев и какое звено (1 или 2) обращено в стойку. Это важное свойство, обусловившее широкое применение высших пар в приборостроении, дает возможность проектировать трехзвенные механизмы более ком­пактными, чем механизмы с одними низшими парами. На рисунке 1.5 показаны два синусных механизма, преобразующих вращение веду­щего звена 1 в поступательное движение ведомых звеньев 2 (рисунок 1.5, а) и 3 (рисунок 1.5, б) по закону S = r·sinφ. Первый из них (с высшей па­рой) - трехзвенный, а второй (с одними низшими парами) - четырехзвенный.

Положительным свойством низших пар является их относительно большая, чем у высших пар, несущая способность. Однако в малонагруженных механизмах приборов это преимущество существенного значения не имеет.

Определим число связей, налагаемых различными парами на относительное движение звеньев. Известно, что любое твердое тело S, если оно не связано с другими звеньями (рисунок 1.6, а), обла­дает шестью степенями свободы (W = 6), т. е. может совершать от­носительно неподвижной системы координат шесть независимых движений: три поступательных (x_а, y_а, z_а ) и три вращательных

(φ, β, α) (угол γ является зависимым, так как cos²α + cos²β + соs²γ = 1), показанных дуговыми стрелками. Если же тело S образует с другим телом кинематическую пару, эта пара свяжет какие-то не­зависимые координаты и уменьшит число независимых движений. Так, если бы тело S оказалось связанным с плоскостью z_а = 0 (рисунок1.6, б), оно потеряло бы одно независимое движение - способ­ность перемещаться вдоль оси z. Связь со второй плоскостью х_а = 0 (рисунок1.6, в) отняла бы у звена еще одну

степень свободы - возмож­ность перемещаться вдоль оси х.

Помещение точки А тела в начало неподвижной системы координат (рисунок 1.6, г) лишает тело S еще одного независимого движения (у_А = 0), и число его степеней свободы становится равным трем: α, β и φ. В результате перевода тела S на плоскость ху путем обращения в нуль угла γ (рисунок 1.6, д) исчезает еще одно независимое движение и остается только два: α, φ. Еще одна связь тела с неподвижной систе­мой координат делает его одноподвижным с независимым вращением α (рисунок 1.6, е) или φ (рисунок 1.6, ж).

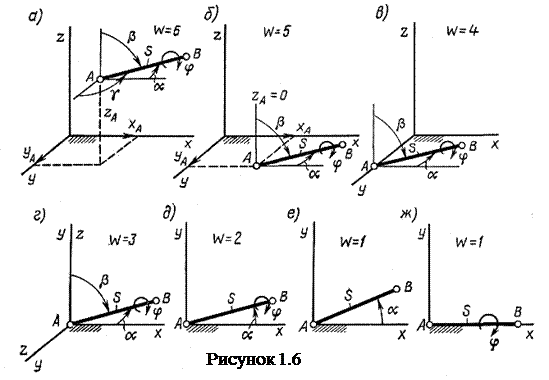Для определения числа связей, которые налагает та или иная пара на относительное движение ее звеньев, одно звено обращают в стойку, после чего устанавливают, какие движения второго звена остались свободными. Очевидно, что число связей, налагаемых на подвижное звено кинематической парой, не может быть больше пяти (рисунок 1.6, е, ж), так как шестая связь обратила бы подвижное звено в стойку.

По числу связей, налагаемых на относительное движение звеньев, кинематические пары делятся на пять классов (таблица 1.1): пары пятого класса (одноподвижные), лишающие относительное движение звеньев пары пяти степеней свободы; четвертого (двухподвижные) − четырех; третьего (трехподвижные) - трех; второго (четырехподвижные) − двух и первого (пятиподвижные) - одной. Число пар k-гo класса в механизме обозначают p_k .