рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- ЛОГИКА
Реферат Курсовая Конспект
ЛОГИКА
ЛОГИКА - раздел Философия, Санкт-Петербургский Государственный Университет Кафедра Логики Филос...
САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
кафедра логики философского факультета
В.И. Кобзарь
ЛОГИКА
Учебное пособие для студентов гуманитарных факультетов
Санкт-Петербург
ОГЛАВЛЕНИЕ
Введение .................................................................................................................... 5
§ 1. О структуре курса логики............................................................................ 15
§ 2. Логика как наука.......................................................................................... 18
§ 3. Методология логики.................................................................................... 25
§ 4. Мышление и язык. «Язык» логики.............................................................. 27
§ 5. Обзор истории логики.................................................................................. 30
Глава 1. Принципы (основные законы) и элементарные методы мыслительной деятельности.............................................................................................. 40
§ 1. Принцип тождества...................................................................................... 42
§ 2. Принцип противоречия................................................................................ 43
§ 3. Принцип достаточности............................................................................... 45
§ 4. Простейшие методы мыслительной деятельности.................................... 45
Глава 2. Понятие........................................................................................................ 49
§ 1. Определение понятия.................................................................................. 49
§ 2. Структура понятия........................................................................................ 52
§ 3. Виды понятий............................................................................................... 54
§ 4. Отношения между понятиями...................................................................... 56
§ 5. Операции с понятиями................................................................................. 60
Глава 3. Суждение.................................................................................................... 71
§ 1. Общая характеристика................................................................................ 71
§ 2. Определение простого категорического суждения, его структура
и виды.......................................................................................................... 75
§ 3. Отношения между простыми категорическими суждениями................... 78
§ 4. Операции с простыми категорическими суждениями............................... 82
§ 5. Модальные суждения................................................................................. 88
§ 6. Сложные суждения...................................................................................... 91
Глава 4. Умозаключение........................................................................................... 97
Дедуктивные умозаключения......................................................................... 100
§ 1. Простой категорический силлогизм и его структура.............................. 100
§ 2. Виды простого категорического силлогизма.......................................... 102
§ 3. Отношения между видами силлогизмов................................................. 108
§ 4. Операции с видами простого категорического силлогизма.................. 111
§ 5. Сокращенные, сложные и сложносокращенные силлогизмы................ 114
§ 6. Условные и разделительные силлогизмы............................................... 119
Глава 5. Индуктивные и традуктивные умозаключения..................................... 123
§ 1. Индукция, ее структурные особенности, виды....................................... 126
§ 2. Методы научной индукции....................................................................... 129
§ 3. Традуктивные умозаключения................................................................. 133
Глава 6. Формы научного мышления.................................................................... 137
§ 1. Проблема (вопрос)..................................................................................... 137
§ 2. Доказательство (опровержение).............................................................. 140
§ 3. Проблема и теория..................................................................................... 154
Заключение.............................................................................................................. 157
§ 1. Логические ошибки.................................................................................... 158
§ 2. Упражнения и задачи................................................................................ 162
Литература................................................................................................................ 173
Сыну и внуку моему, а в их лице -
"племени младому, незнакомому"
посвящается.
ВВЕДЕНИЕ
Слово "логика" большинством воспринимается как название науки о правильном мышлении. Желание правильно мыслить естественно и даже похвально. Но чтобы научиться правильно мыслить, надо знать правила, которым мысли подчиняются. Правила же лишь тогда будут полезны, когда предметная область их приложения четко осознается. И здесь возникает довольно сложная проблема: что же такое мысль, мышление? То же самое, что речь, «слово», которыми мы постоянно пользуемся, или нечто отличное от них?
Что слово не тождественно тому предмету, который оно обозначает (замещает его), достаточно очевидно. А смысл слова, хотя и теснейшим образом связан со словом, но все-таки не есть само слово, так же смысл слова не есть и сам тот предмет, признаки которого он отражает. Смысл (мысль) - нечто незримое, неосязаемое. Что же тогда?... Незримость мысли, не воспринимаемость ее органами чувств привносит значительные трудности и в понимание логики.
Слово "логика" в повседневной речи часто означает для нас взаимосвязанность, последовательность и не столько как простая, текучая непрерывность, сколько следование по необходимости. Когда говорят или признают: "логично", - то имеют в виду, как главное, что нечто следует из предшествующего обязательно. В этом смысле логичное (обязательное, необходимое) бывает лишь тогда, когда оно обуславливается тем или иным законом: то ли законом связи букв и слов в предложении, то ли законом связи между мыслями в рассуждении, то ли законом природы, то ли общественным законом.
Повседневное общение - это, как правило, разговор (речь), т.е. обмен словами, предложениями, но он же есть и обмен мыслями по поводу тех или иных предметов (на ту или иную тему), поскольку слова и предложения речи, обозначая, заменяя предметы, несут еще и определенную смысловую нагрузку. Мысли и слова, как ни крепко и тесно они связаны друг с другом, тем не менее, далеко не одно и то же. Мысли, будучи по природе своей непосредственно не наблюдаемым, идеальным образованием, в словах и предложениях находят свое материальное выражение. Конечно, мысли материализуются не только в речи, но во всей жизнедеятельности человека, в его практической, производительной деятельности, в продуктах труда. И Г.Гегель был совершенно прав, выступая против упрощенного представления о мышлении как только речевой деятельности. Реально мышление проявляет себя и в теоретической, и в практической деятельности человека.
Обнаружение "логики" в речи может означать и то, что человек, говоря на том или ином языке, соблюдает законы (правила) этого языка. Он правильно связывает буквы и звуки в словах, слова в предложениях, наконец, предложения друг с другом в процессе речи. Эти правила (законы) раскрывает, формулирует их и вооружает ими нас грамматика того или иного языка. Если правила соблюдаются, то человек говорит культурно, правильно (логично). Но это одна "логика", назовем ее грамматической. Другая логика связана с соблюдением в процессе речи законов связи и мыслей между собой. Но что такое мысль и какие законы относятся к ней?
Что касается грамматических правил (законов), то они всем давно известны, их изучают еще в начальной и средней школе на уроках родного языка. А вот законы (правила) связи мыслей, определенно, еще не изучались, поэтому в обыденной повседневности их почти никто и не знает, более того, большинство даже и не подозреваем об их существовании, что и понятно: как можно знать суть того, что еще не известно.
Мысль - явление столь специфичное, что в определенной мере его можно рассматривать и как явление таинственное. Проблема мысли та же, что и проблема души, духа и т.п. Поскольку это не предмет логики как науки, она и не решает его, а заимствует понимание и определение мысли из философии. Последняя характеризует мысль как обобщенный, отвлеченный, абстрактный, идеальный "образ" чего бы то ни было, существующий, естественно, только в голове человека. Этот "образ", конечно же, приходится понимать не как фотографию, не как карту, схему, таблицу и т.п., а более общо и отвлеченно - как умозрительный образ; так в свое время мы осознавали, что такое "треугольник", "плоскость" и т.п., поскольку в природе их самих по себе нет. При этом не следует никогда упускать из виду, что мысль не тождественна ни слову, в котором она лишь выражается, ни предмету, который она лишь отражает, хотя мысль, слово и предмет теснейшим образом взаимосвязаны.
Идеальность мысли и является одной из главных трудностей при осознании специфики ее, ибо это - та трудность, преодолеть которую нельзя, просто перешагнув через нее, а лишь пропустив ее через себя. Без твердого осознания специфики мысли, ее идеальности, дальнейшее движение по освоению логики будет безуспешным. "Сидящий" же, условно говоря, в каждом молодом человеке стихийный материалист не соглашается с этим.
Итак, если мысль есть идеальный образ, то его органами чувств, естественно, никто обнаружить не в состоянии. Мысль можно лишь осмыслить, или помыслить, мысль можно понять только мысленно. Раз мысль идеальна, бестелесна сама по себе, то ее как таковую не только нельзя ощутить (наблюдать и пр.), но, строго говоря, и передать на расстояние. А в этом случае, как же мы общаемся, понимаем, находясь на расстоянии, друг от друга?
Понимание наступает тогда, когда находятся средства, способы материализации находящихся в голове мыслей, и это материальное, т.е. слова и предложения, а короче - язык, или иные знаковые системы, являющиеся по природе своей материальными, мы передаем на любое расстояние. Таким образом, естественный язык для каждого человека выступает средством материализации его мыслей, а так как материальное (знаки, буквы, звуки, слоги, слова и предложения) допускает многообразные с собой действия, то слова (речь) можно произносить, записывать, хранить, преобразовывать, искажать и передавать. Но строго говоря, передаются при этом не мысли сами по себе, а вещественные (материальные) знаки мыслей, которые воспринимаются другими и, только если они владеют данным языком, то уже в их головах эти знаки преобразуются в адекватные источнику мысли. Без знания соответствующего языка, все эти воспринимаемые знаки так и могут остаться для нас бессмысленным набором символов, звуков, букв и пр.
Язык, тем самым, выступает в нескольких функциональных значениях: он является знаковой системой по обозначению, по замещению предметов, явлений, процессов действительности, и в то же время он носитель (выразитель) мыслей об этих предметах. Каждый человек, овладевающий разговорной речью, научается, пользуясь вместо предметов словами, манипулировать ими, что, естественно, легче делать, чем "ворочать" самими предметами.
Однако, и здесь не все так гладко. Хотя значения слов и более стабильны, чем смысловые их оттенки, но и значения одних и тех же слов могут быть разными, тем более, что смысловые оттенки столь зависимы от контекста, что могут приобретать даже противоположное значение или смысл, т.е. положительные по смыслу слова текста "говорят" об отрицательной характеристике чего-то или кого-то. Смысл слова, скорее всего, и есть то, что мы называем мыслью, хотя у логиков и лингвистов здесь нет еще полной согласованности.
Если попытаться представить эти взаимоотношения наглядно, то предмет, слово для его обозначения и смысл слова, отражающий свойства предмета, можно выразить такой схемой:
предмет
слово смысл
(мысль)
Таким образом, мысль о предмете выразима в слове, которое обозначает (замещает, заменяет) предмет, и в то же время материализует мысль. Отдельная мысль о предмете не может отразить все бесконечное многообразие присущих ему признаков и свойств, поэтому она отражает только наиболее важные, общие и в то же время отличительные, одним словом - существенные. Существенными являются те, которые отражают природу предмета, его внутренние, главные, коренные, необходимые свойства, изменение которых качественно меняют сам предмет.
Итак, логично будет, если рассуждая о том или ином предмете (как вещественно-материальном, так и мнимом, невещественном, нематериальном), будем свои мысли облекать в знаковые системы, правильно (по правилам, по законам) связанные между собой. В реальности делать это несложно, правила естественного языка (этой знаковой системы) давно известны. Значительно сложнее соблюдать правила связи между мыслями, ибо правила-то нам пока и не известны. Однако, теперь, хотя бы в первом приближении, мы знаем о специфике мысли, и поэтому правила языка не будем распространять на мысли, так же как и законы предметного мира тоже не будем распространять ни на слова, ни на мысли: закону тяготения, например, ни мысли, ни слова не подчиняются. Здесь необходим лишь небольшой тренинг на примерах, и вскоре каждый будет в состоянии отличать свойства слова от свойств предмета, словом обозначаемого и, наоборот, свойства предмета отличать от свойств слова.
Осознание специфики мысли, ее отличия и от предмета, который мыслью отражается, и от слова, в котором мысль выражается, позволят сосредоточиться только на мысли. Попытаемся теперь выявить, какие же законы присущи мыслям, каким законам они подчиняются, какими законами они регламентируются.
Мысль как идеальный образ может быть простой (отдельной) или сложной, состоящей из нескольких простых. Простая (отдельная) мысль отражает, как уже отмечалось, предмет в его существенных и отличительных признаках. Такие мысли в логике называются понятиями, как например, мысль о человеке, о столе, о доме и т.п. Такие мысли обычно выразимы отдельными словами или словосочетаниями: "дом", "стол", "человек", "дневное светило", "самый крупный город в нашей стране", "студент дневного отделения первого курса" и т.п.
Сложные мысли образуются из нескольких простых, связанных между собой определенным (по логике определенным, т.е. логичным) образом. Логика выделяет следующие более сложные мысли: суждение (простое и сложное), умозаключение (дедуктивное, индуктивное, традуктивное), доказательство и опровержение, гипотезу, теорию и некоторые другие. В них и между ними логика выделяет следующие связи и отношения: для простых суждений - совместимость, т.е. тождественность, подчиненность, частичное совпадение, они выразимы логической связкой "есть"; и несовместимость, т.е. противоречие, противоположность, соподчинение - они выразимы логической связкой "не есть". Для сложных суждений - соединение (логический союз "и"), разделение (логический союз "или"), условную связь ("если..,то") и связь тождественности ("тогда и только тогда, когда").
Кроме этих логических связей, выделяет логика и связи по среднему термину, по основанию и следствию, по члену деления и пр., которые могут стать понятными лишь при более обстоятельном знакомстве со строением этих сложных форм мысли, что и составит содержание учебника по логике.
Каждая из форм мысли (простая или сложная) имеет свое специфическое строение, свою структуру и, соответственно этому, свои как внутренние, так и внешние законы, свои признаки и свойства.
Так как любая наука, изучая ту или иную предметную область, выявляет законы этой предметной области, а законы - вещь общая, повторяющаяся, то, зная их, используя их, можно будет оптимизировать нашу интеллектуальную деятельность как в процессе рассуждения, так и в процессе ее анализа. Не зря, ведь, еще в период средневековья была сформулирована Роджером Бэконом (некоторые связывают это с Френсисом Бэконом) мысль: знание - сила! Если мы будем знать и соблюдать законы мысли (законы связи между мыслями), определенно, наши рассуждения будут строже, точнее, научнее, т.е. логичнее.
Как же обнаружить эти законы? Для этого надо знать все виды, обычно их называют формами, мысли и изучить каждую из них. Но в процессе рассуждения мысли постоянно видоизменяются и их трудно исследовать. Поэтому в науке (и в "Логике", раз уж она наука) принято рассматривать свой предмет в статике и в определенной последовательности, как правило, от простого к сложному. В нашем случае, простой формой мысли является понятие, более сложными - суждение, рассуждение (умозаключение), доказательство и т.д.
Структуры форм мысли без специальной подготовки трудно выделимы. Подготовив нас к ориентации в структуре языковых форм, мысленные средняя школа совсем не затрагивала. Поэтому эти формы, хотя они постоянно сопутствуют нашей речи, так трудно уловить в процессе разговора, полемики, внутренней речи, рассуждения, короче - в процессе дискурса.
Научный подход, научный метод исследования всегда требует расчленения (анализа) сложного до простейшего, до "единицы", до "элемента". Потом, на основании обстоятельного исследования "единицы", на основе полученных знаний о ее строении, свойствах и признаках, из этого простейшего синтезируются более сложные структуры, которые исследуются в том же порядке, но это исследование реализуется значительно легче, так как уже известно главное в его строении - основная "единица" структуры.
В итоге, мы как бы возвратимся к исходному (к речи, рассуждению, дискурсу), но это возвращение произойдет уже на основе знания каждого, входящего в речь (рассуждение, дискурс), структурного элемента. Это возвращение будет более высокой ступенью осознания (осмысления) предмета нашего исследования, так как при этом можно воспользоваться всем богатством накопленного до этого о нем знания. И если первоначально речь, рассуждение были для нас чем-то в своей общности и текучести неопределенным и нерасчлененным, то после аналитического исследования его составных частей, оно предстает как закономерная связь входящих в него элементов; знание предмета нашего изучения становится более конкретным, более определенным, более обстоятельным.
Во все времена слово "логика" было неоднозначным, таково оно и сейчас. Неоднозначно и выражение "наука логика". После "Науки логики" Г.В.Гегеля чаще приходится пользоваться более сложным выражением "логика как наука", чтобы отличить ее от "науки логики" Гегеля и от двух других значений слова "логика". "Логика науки" тоже не совсем определенное выражение, хотя им и часто пользуются. Скорее всего, его можно понимать как указывающее на что-то необходимое, закономерное, присущее любой отдельной науке, ее истории, ее строению, ее развитию, динамике; но может быть - это общие закономерности науки вообще. Таким образом, выражение "логика науки" может быть отнесено и к отдельной науке и к науке вообще. Если к отдельной науке, то данное выражение выделяет специфические особенности возникновения, формирования и развития именно этой науки, и они, возможно, неповторимы, уникальны, отражают специфику предметной области только этой науки. Если к науке вообще, то данное выражение выделяет, наоборот, общие закономерности и особенности развития всех наук. Всеми этими выражениями нам придется пользоваться, и часто только контекст будет определять (уточнять) значение их.
Итак, если мы рассматриваем то или иное рассуждение, текст, речь о чем-то, например, вот этот фрагмент: "Однажды весною, в час небывало жаркого заката, в Москве, на Патриарших прудах появились два гражданина" - мы должны прежде всего выяснить для себя, о чем здесь речь, что есть предмет речи (рассуждения), т.е. предмет мысли. Понятно, что здесь в довольно пространном предложении, говорится всего лишь о двух гражданах, появившихся в определенное время в определенном месте.
Если это предложение изобразить в каком-то условном, например, символическом виде, то выражаемая этим предложением мысль получит очень короткую форму: S (предмет мысли) обладает свойством Р (признак предмета мысли), т.е. "S есть Р". Получается, что сколь бы ни была сложна речь, рассуждение, основное в них символами может быть выражено довольно кратко. Для нас это важно, потому что символическое выражение, отражая главные элементы строения мысли, не отвлекает нас на второстепенное с этой точки зрения, например, содержание, хотя оно может быть и очень важно, но уже по другим, поэтическим ли, художественным или иным критериям. Задача же логики - строение мысли, структура ее.
Таким образом, символом S мы обозначили предмет нашей мысли (предмет речи, высказывания и пр.), а символом Р - признак, этому предмету присущий (или не присущий). Между этими двумя элементами мысли, в логике их принято называть субъект и предикат, явно или неявно присутствует определенное отношение. В нашем примере это отношение выражено словом "появились", что соответствует утверждению ("есть" и т.п.), хотя могло быть и отрицание ("не есть"). В русском языке отношение может выражаться разными словами, а порой и просто опускаться: Жучка - собака, студенты - учащиеся.
Далее, в рассматриваемом примере субъект выражен двумя словами, словом "два" и словом "гражданина", а предикат - куда как большим количеством слов. Но, выраженная в виде формулы "S - Р", эта мысль имеет всего три элемента: субъект (предмет мысли), предикат (признак предмета мысли) и связку, или отношение между ними - "есть" ("появились").
Мысль о двух гражданах есть мысль отдельная, простая, в ней отражается как количественная, так и качественная сторона нашего предмета мысли. Количественная сторона в логике называется объемом мысли, качественная - содержанием. Объем рассматриваемой мысли ограничен словом "два", в содержание же этой мысли войдут все признаки, присущие любым гражданам.
Теперь важно установить, каково же отношение между этими элементами в той или иной отдельной мысли. Простое рассуждение показывает, что в мысли о гражданине вообще (о любом гражданине нашей планеты) общих признаков будет значительно меньше, чем если бы разговор шел о гражданах России, ибо мысль о гражданине вообще не может отражать, как не общие, такие признаки как цвет кожи, глаз, национальность и пр., но чем меньше будет объем этой мысли, например, "гражданин России", тем больше признаков будет входить в ее содержание. Поэтому, самое меньшее содержание будет в самой общей по объему мысли, а самое богатое содержание будет в единичной мысли, в мысли об индивидуальном предмете. В итоге, мы необходимо приходим к выводу, что любая отдельная простая мысль есть единство ее объема и содержания, всегда находящихся в отношении обратной зависимости. В логике такая отдельная, простейшая мыслительная форма называется понятием и определяется как мысль, отражающая существенно-отличительное в предмете, а так как предметом мысли может быть все, что угодно, то можно сказать "отражающая существенно-отличительное в чем угодно". Понятие как одну из простейших форм мысли можно определять по-разному: и как мысль, отражающую существенно-отличительные признаки чего бы то ни было; и как мысль, структура которой есть диалектическая связь (обратная зависимость) противоположных элементов (объема и содержания); и как мысль, выражающаяся в языке отдельным словом или словосочетанием. Но подлинно научным определением понятия как формы мысли является все логическое учение о данной форме мысли -- теория логики о понятии. Подробнее об этом будет сказано в главе о понятии.
Объединение S и Р связкой "есть" формирует более сложную мыслительную структуру, более сложную форму мысли, которую в логике называют суждением. Различают простые суждения и сложные. Простые, в свою очередь, подразделяются на категорические, суждения существования и отношения. Формула "S – Р" есть выражение структуры простого категорического суждения. Чтобы понять особенности и законы этой структуры, необходимо исследовать и понятие как составную часть этой структуры, а потом и всю эту новую форму мысли уже как единство двух входящих в нее понятий.
В нашем содержательном примере из текста М. Булгакова количественный показатель субъекта данной мысли оговорен. Когда бы он не был оговорен, то по логике мы обязаны были бы уточнить этот показатель, потому что при анализе структуры любой мысли нельзя ничего, относящегося к элементам структуры этой мысли, упускать из виду или пропускать. Главными элементами строения этой, несмотря на многословие, все таки, простой мысли являются S и Р, т.е. два отдельных понятия: понятие, отражающее предмет нашей мысли и понятие, отражающее признак этого предмета. Третьим элементом этой мысли является связка (или отношение) между ними, в нашем случае она выражена утверждением "появились". Таким образом перед нами простое категорическое утвердительное суждение, а с учетом количественного показателя субъекта, так называемого квантора, - простое категорическое частноутвердительное суждение. Квантор подразделяет суждения на три разновидности: единичное, частное и общее.
Единичность субъекта выразима в языке словами "этот", "один", "данный", "единственный" и пр., хотя может и не иметь явного выражения, определяясь контекстом. Множественность тоже выразима разными словами: "некоторые", "существуют такие", "не все", "большинство", "меньшинство", "часть", "два" и т.п., но в логике преимущественно используют всего лишь два из этих выражений, а именно: "некоторые" и "существуют такие". Для отображения же всего объема предметной области, всего множества субъектов, используются слова "все", "без исключения", "ни один", "всякий", "каждый" и т.п. Количественные показатели в логике обобщенно называют квантором и различают всего два его вида: квантор общности ("все" и пр.) и квантор существования ("некоторые" и пр.). Единичное суждение в логике обычно включают в общее и отдельно не рассматривают, поэтому в логике и нет квантора единичности.
Из нескольких простых суждений могут состоять сложные. Поскольку мы уже знаем структуру простого суждения, то при изучении сложного, состоящего из нескольких простых, структуру простого можно, условно говоря, "сжать", обозначив его всего лишь каким-нибудь символом, или буквой, например, В. Тогда становится ясным, что главным отличительным элементом сложного суждения будет выступать новая логическая связь между простыми суждениями, которую в логике и называют "логический союз", ибо он формирует, связывает между собой несколько простых суждений. В логике различают всего лишь четыре логических союза: соединительный, разделительный, условный и тождественности.
При анализе сложных суждений нет необходимости детально анализировать входящие в него простые, поскольку они уже известны, поэтому их обычно и обезличивают, оставляя за ними только одно неотъемлемое их свойство - быть либо истинными, либо ложными. Например, В (символ для одного простого суждения - "S есть P") можно связать разделительным союзом или с символом С (другое простое суждение - "S есть P1") и получить в итоге сложное суждение, читаемое "В или С". Такова формула сложного суждения и понятно, что ее проще анализировать, чем если бы записывали: "S есть Р или S есть Р1".
С помощью новых логических связей из нескольких то ли простых, то ли сложных суждений формируются еще более сложные мыслительные формы - умозаключения (рассуждения). И в них главным элементом выступают логические связи, поскольку они-то и создают новую форму, новую мыслительную конструкцию. Эти логические связи будут обстоятельно рассмотрены в соответствующих разделах учебника, сейчас же лишь дается общее представление о предмете логики как науки, в который входят и эти связи.
Помимо последовательности рассмотрения форм мысли - от простой к сложной, - немаловажна для логики и последовательность рассмотрения каждой формы мысли в отдельности. В "Логике", ведь, логичным должно быть все, и содержательное ее наполнение (что достаточно естественно), и внешнее структурное оформление этого содержания. Но вот оно-то многими совершенно выпускается из виду. Поэтому, в одних учебниках логическое содержание начинают излагать с понятия, в других - с суждения, в третьих - с формулировки основных законов мышления (основных законов логики) и т.п. Правда, эта непоследовательность зачастую обосновывается различными философскими взглядами на простейшую форму мысли, поэтому ее можно и не считать столь уж важной. Но другая последовательность, последовательность рассмотрения каждой формы мысли в отдельности, внутрисодержательная последовательность, выдерживается и того меньше. Между тем, она более всего подчеркивает логичность в содержании самой логики.
Со времени создания логики как науки, а особенно со времени превращения ее в учебную дисциплину, остро встала не всегда явно осознаваемая задача - нахождение наиболее оптимального и эффективного способа ее преподавания. Похоже, эта задача мало занимала внимание специалистов, хотя явно, что она существенна, важна. От нее в немалой степени зависит не только эффективность преподавания, но и успешность использования этой науки, ее практическое применение изучающими. Трудно, ведь, согласиться с тем, что логика преподается только ради нее самой, или ради престижа, но так же трудно не признать и крайне низкую результативность овладения этой наукой.
Причин, обуславливающих эту неэффективность много. Предпочтительнее сосредоточиться на той, которая менее всего должна быть присуща этой науке, но которая на протяжении веков была неотъемлемой для ее изложения. Здесь имеется в виду, конечно же, определенная последовательность оформления, структурирования ее содержания в учениках и учебных пособиях, а также и определенная последовательность изложения этой науки в процессе преподавания. Поскольку логичное, логика - это обязательно необходимая, закономерная связь, то таковой должна быть связь и внутри самой науки логики между различными элементами ее содержания. Это то, что может быть названо "логика логики"; другими словами, логика должна не только формулировать нормативы, закономерности для различных мыслительных структур (для других наук), но и сама должна по этим же нормам (закономерностям) структурировать свое содержание. Если науки есть системы определенным образом упорядоченного знания, то, согласно понимания структуры как закономерной связи элементов внутри целого, все содержание той или иной науки (система ее знания) должно быть увязано внутри себя по определенному закону. Логика как особая наука, выполняющая методологическую роль по отношению к другим наукам, должна представлять собой образец подобной внутренней упорядоченности.
Прежде всего, конечно, нужно установить составляющие элементы нашей науки, а уж потом и устанавливать определенную взаимосвязь между ними. К числу элементов науки логики, помимо основного предмета ее исследования - форм мысли, можно отнести:
принципы (основные законы), принимаемые или разделяемые этой наукой;
используемые ею методы, т.е. инструментарий данной науки;
ее основные понятия (категории), т.е. "язык";
открываемые в рамках самой науки внутренние законы, законы ее предмета (законы форм мыслей);
доказанные в рамках самой науки положения - определения, или теоремы;
ошибочные (неправильные) мыслительные структуры, просто ошибки.
Поскольку предмет формальной логики специфичен, он невещественен, идеален (мысли, ведь, сами по себе в природе не существуют, визуально их не воспринять, не потрогать, не взвесить, не измерить и пр.), то соответственно этой природе необходимы и особые средства исследования предметного поля логики нужны особые критерия различения элементов внутри этого "поля".
Предметом изучения логики являются формы мысли, которыми пользуются люди в своей интеллектуальной и практической деятельности. Форм этих несколько, среди них одни проще по своему строению, другие сложнее. Последовательность рассмотрения этих форм тоже предполагает определенность. А между тем, как уже отмечалось, в большинстве учебников и учебных пособий по логике последовательность рассмотрения форм мысли редко бывает одинаковой, что невольно наталкивает на мысль: не есть ли это показатель нелогичности, т.е. отсутствие закономерной упорядоченности между формами мысли. Мы будем выдерживать в этом плане общенаучный принцип рассмотрения предмета: от простого к сложному, т.е. раз понятие есть элемент суждения как формы мысли, а суждение, в свою очередь, элемент умозаключения, то и рассматривать мы их будем в последовательности: понятие, суждение, умозаключение.
Однако, установление упорядоченности (закономерности) в связях между формами мысли не исчерпывает всех закономерностей логического материала. Не менее важна и необходимая последовательность при рассмотрении каждой из форм мысли. Тенденция такой закономерности просматривается во многих учебниках и пособиях по логике, но четко и явно она не оговаривается и не выдерживается. А ведь логическое, подчеркиваем еще раз, по природе своей - это обязательно упорядоченное, необходимое, закономерное.
Отмеченные особенности нашей позиции определяют не только последовательность рассмотрения форм мысли, но накладывают свой отпечаток и на рассмотрение некоторых особенностей самих форм и методов мысли.
О СТРУКТУРЕ КУРСА ЛОГИКИ
Изданные в последние годы учебники и учебные пособия по логике, несмотря на обилие присущих им достоинств, имеют все же общий недостаток — некоторую… Общенаучная последовательность изложения материала от простого к сложному… Вторая последовательность изложения содержания логики, как правило, не оговариваемая, но иногда обнаруживаемая в…ЛОГИКА КАК НАУКА
Слово "логика" для обозначения науки о мышлении, о формах и законах его, ввел в самом начале III в. до н.э. основатель стоического… В русском языке слово «логика» используется для обозначения: а) необходимой, закономерной связи предметов и событий в окружающем мире, связи последующего с предыдущим (логика…МЕТОДОЛОГИЯ ЛОГИКИ
Логика занимает особое место в системе наук. Особенность положения определяется тем, что логика, как и философия в целом, выполняет по отношению к… Во-первых, как совокупность методов, используемых и той или иной науке. В… Во-вторых, как учение о методах. В этом смысле методологией обладают только философия и логика, ибо философия…МЫШЛЕНИЕ И ЯЗЫК. "ЯЗЫК" ЛОГИКИ
Как уже подчеркивалось, мысли сами по себе не имеют вещественно-телесной формы выражения, т.е. не существует мыслей в виде некоего самого по себе… Мышление неотрывно от языка. Мышление и язык исторически и генетически… Поскольку каждая форма мысли имеет свое языковое выражение, то обстоятельнее мы это рассмотрим позже, когда дойдем до…ОБЗОР ИСТОРИИ ЛОГИКИ
Общеизвестно, что подлинное знание той или иной науки (дисциплины, предмета) предполагает знание не только сущности этой науки, т.е. ее структуры,… Хотя первые учения о рассуждении, о формах и способах (методах) мышления… Принято именно Аристотеля (384—322 до н.э.) считать отцом логики, хотя Аристотель, как известно, учился у Платона,…ПРИНЦИПЫ (ОСНОВНЫЕ ЗАКОНЫ) И ЭЛЕМЕНТАРНЫЕ МЕТОДЫ МЫСЛИТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
Каждой науке соответствуют определенные положения, принимаемые в этой науке без доказательства, без обоснования — в силу их фундаментальной… Другое дело, когда, учитывая особенности предметной области логики, эти… Осваивая принципиальные положения (основные законы) логики, важно знать особенности исторического их осознавания и…ПРИНЦИП ТОЖДЕСТВА
Итак, первым принципом логики как науки является положение: всякая мысль тождественна сама себе. В виде формулы этот принцип записывается - "А… В качестве следствий принципа тождества можно сформулировать следующие… Противоречит ли закон тождества диалектическим законам? Учитывая своеобразие предмета логики, легко установить, что…ПРИНЦИП ПРОТИВОРЕЧИЯ
Закон тождества находит свое проявление во многих положениях логики. Можно сказать, что и в законе противоречия легко просматривается закон… Какие же мысли не тождественны между собой? Конечно же, противоречащие мысли.… Закон исключенного третьего: противоречащие мысли не могут быть одновременно ни истинными, ни ложными, т. е. если…ПРИНЦИП ДОСТАТОЧНОСТИ
В литературе по логике нет разночтений по первым трем законам, они были известны еще Аристотелю и в разных формулировках встречаются в его работах,… Обе формулировки носят явно выраженный онтологический характер, поэтому о…ПРОСТЕЙШИЕ МЕТОДЫ МЫСЛИТЕЛЬНОЙ ДЕЯТЕЛЬНОСТИ
Если принципы выполняют роль фундамента, основы здания науки, то методы - роль инструментария, роль средств строительства этого здания. Ими… Освещая простейшие (элементарные) методы мыслительной деятельности,… В большинстве учебников и учебных пособий по логике, как правило, анализ, синтез и другие методы рассматриваются в…ПОНЯТИЕ
Проблема простейшего элемента той или иной системы, той или иной науки исследовалась давно. В ее разработку внесли свой вклад Аристотель, Ф. Бэкон,… Такая точка зрения является результатом нечеткого, нестрогого понимания… Поскольку понятие состоит всего лишь из двух элементов, а суждение составляют как минимум два понятия, и в нем еще…ОПРЕДЕЛЕНИЕ ПОНЯТИЯ
Понятие есть форма мысли, отражающая общие, существенные и отличительные признаки чего бы то ни было, что может быть предметом нашей мысли. Понятие… Общими признаками (свойствами) являются те, которые присущи хотя бы нескольким… Существенным по природе предмета признаком будем считать тот, который отражает внутреннее, коренное свойство предмета,…СТРУКТУРА ПОНЯТИЯ
Как цельная форма мысли понятие представляет собой закономерное единство двух составляющих его элементов: объема и содержания. Объем — структурный… Закономерная связь объема и содержания понятия определяет целостность данной… Обратное отношение объема и содержания понятия выступает главным законом структуры данной формы мысли. Такие законы…ВИДЫ ПОНЯТИИ
За счет изменения одного из элементов структуры понятия последние могут подразделяться на виды. Так, по количественному признаку (по объему) понятия… Единичными понятиями являются те, которые отражают всего лишь один… Общими понятиями являются те, объемы которых отражают два и более однородных предмета (явления, процесса) вплоть до…ОТНОШЕНИЯ МЕЖДУ ПОНЯТИЯМИ
Перечисленные виды понятий находятся между собой в определенных отношениях, и прежде всего в отношении сравнимости и несравнимости. В отношении… В отношении несравнимости находятся те понятия, ни в объеме ни в содержании… Среди сравнимых понятий легко выделимы понятия, находящиеся в отношении совместимости и несовместимости. Совместимые…ОПЕРАЦИИ С ПОНЯТИЯМИ
Накопленные знания о понятии, об этой элементарной форме мысли позволяют нам воспользоваться ими для самого главного - для оперирования (действования, или действия) с ними. Все раннее полученные знания о понятии, рассматриваемые по отдельности, представляют собой односторонние сведения о нем, это, говоря на языке философии, абстрактные в этой односторонности, неполноте знания. Только в совокупности своей они представляют богатое определениями знание о данной форме мысли и в этом богатстве выступают как знание конкретное. Вот это знание и следует использовать для действий, для оперирования понятиями.
Обычно к операциям с понятиями (или над понятиями) относят отрицание, умножение, сложение, вычитание, обобщение, ограничение, деление и определение. Операции - самая важная (порой и самая сложная) часть учения о понятии, затрагивающая либо один элемент понятия, либо оба сразу.
Простейшей логической операцией с понятиями является отрицание. Операция осуществляется простым прибавлением к любому исходному понятию отрицательной частицы «не». Данная операция может производиться неограниченное число раз с одним и тем же понятием. Учитывая специфику мысли, ясно, что всякий раз при этом отрицание отрицательного понятия дает положительное понятие, т.е. двойное отрицание снимается, или нейтрализуется. Так, отрицание отрицательного понятия «не-студент» даст в итоге понятие «не-не-студент», являющееся по существу положительным понятием «студент». Операция отрицания, таким образом, сколько бы раз она не совершалась, все равно дает только два возможных вида понятия: утвердительное или отрицательное. Некоторые авторы положительное и отрицательное понятия рассматривают как дополнительные. В этом смысле, например, понятие «успевающий студент» и понятие «неуспевающий студент», дополняя друг друга, отражают универсальную для них область — объем понятия «студент».
К числу простейших логических операций с понятием следует отнести сложение, вычитание и умножение понятий. Операция сложения представляет собой объединение объемов двух или более понятий, даже если эти понятия и не пересекаются, не совпадают между собой по объему. Так, объединив понятие «школьник» и понятие «студент», мы получим область, отражающую признаки, присущие тому и другому понятию в рамках общего для них родового понятия «учащийся». В наглядном виде эта операция дает заштрихованную область на схеме:
Ш С
У
Операция умножение состоит в отыскании области, которая обладает одновременно свойствами как одного, так и другого понятия. Так, умножение понятий «студент» и «спортсмен» дает область студентов, являющихся в то же время спортсменами, и наоборот. Схематически:
Ст СП
Вычитание объема одного понятия из объема другого даст, в зависимости от видов рассматриваемых понятий, усеченную область объема. Вычитание возможно только между совместимыми, а точнее - между пересекающимися и подчиненными понятиями. Так, вычитание объема понятия «студент», из объема понятия «учащийся», дает такую область:
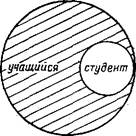
Вычитание объема понятия «студент» из объема понятие «спортсмен» дает несколько иную область:
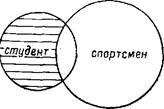
Понятно, что результат вычитания тождественных понятий нельзя представить наглядно.
Обобщение рассматривается в логике и как метод, и как операция с понятием. Как операция с понятием обобщение заключается в увеличении объема исходного понятия — это переход от понятия с меньшим объемом к понятию с большим объемом за счет, естественно, уменьшения содержания исходного понятия. Так, переход от понятия «студент» к более общему понятию «учащийся» или «человек» совершается путем отбрасывания одного или нескольких содержательных признаков исходного понятия. Таким образом, увеличение объема понятия, т.е. обобщение, в тоже время есть и уменьшение содержания. Пределом обобщения выступают категории философии как наиболее широкие по объему понятия. Категории - это высший род, и с какого бы понятия мы не начали обобщение, конечным результатом его будет та или иная философская категория. В нашем примере, продолжая обобщение понятия "студент", мы получим после понятия "человек" понятие "примат", "млекопитающее", "позвоночное", "животное", "живой организм", наконец, "материя". Далее обобщить невозможно.
Обратная обобщению логическая операция ограничение есть переход от понятия с большим объемом к понятию с меньшим объемом. Ограничение совершается прибавлением к содержанию исходного понятия одного или нескольких новых признаков. Так, если к содержанию понятия «студент» прибавим хотя бы такой признак, как обучение в университете, то получим новое, содержательно более богатое понятие «студент университета». Продолжая эту операцию, можно получить понятие «студент Санкт-Петербургского университета» (студент СПбГУ), «студент СПбГУ гуманитарного факультета», «студент СПбГУ философского факультета», «студент СПбГУ 1-го курса философского факультета» и так вплоть до понятия о конкретном, отдельном студенте. Ясно, что пределом ограничения выступает единичное понятие, ограничить которое невозможно. Единичное понятие при минимуме объема имеет самое богатое содержание, наибольшее количество признаков. Такое понятие называется низшим видом, индивидом.
Несмотря на то, чти пустые (нулевые) понятия своим объемом не отражают реально существующие материальные объекты, тем не менее, как мысли они могут быть и обобщены. и ограничены. Например, нулевое понятие «кентавр» может быть обобщено — «мифологический образ», может быть ограничено — «кентавр Беотии», «кентавр Хирон». В подобных случаях мы имеем дело с мысленными формами, а мысли сами по себе, независимо от того, отражают они реальность или порождают ее в виде мнимых, нереальных, воображаемых предметов, как мысли они обладают собственными, отличными от предметов, свойствами. Мысли приобретают относительную самостоятельность и с ними можно производить определенные действия. Обобщение и ограничение пустых понятий дают, как правило, тоже пустые единичные или общие понятия. Обобщаются и ограничиваются и абстрактные понятия, но обобщаются они, как правило, сразу философской категорией «свойство», или "признак", "качество", а ограничение может быть доведено до единичности, до индивида.
Деление — логическая операция, раскрывающая объем понятия, это распределение объема исходного понятия на виды, группы, классы, части по единому для них признаку (основанию деления). В делении различают делимое понятие, основание (признак) деления и члены деления. Основанием деления должен быть общий для всех членов деления признак; видоизменение этого признака как раз и отличает один член деления от другого. Наличие основания деления отличает эту операцию от простого расчленения предмета на части. Рубль, например, мы можем разделить на составляющие его полтинники, гривеники, копейки и пр. Деление, конечно, тоже расчленение, но особое, и не предмета, а объема понятия и при этом еще по особому признаку. Деление понятия в логике — это такое раскрытие объема его, где каждый член деления, как составная часть объема понятия, сохраняет свойства делимого, т.е. целого, в то время как расчленение предмета дает такие части, которые не обладают свойствами целого (расчленяемого, делимого). Копейка, например, в отдельности, гривенник или полтинник не составляют рубля, а разделенное по объему понятие "рубль" дает в результате такие группы как "бумажный" или "металлический рубль", которые полностью сохраняют свойства делимого понятия, его содержательные признаки. Минута не составляет часа, она лишь шестидесятая часть его, поэтому понятие «час» не делится по объему на «минуты», не включает в свой объем понятие «минута». Понятие «час» может быть распределено по объему на «час академический», «час астрономический», «час учебный» и пр. Тут все члены деления сохранили свойства делимого, а вот части этого предмета — «минута», «секунда» и пр., каждая в отдельности, естественно, часом не являются. Делению поддаются общие понятия, единичные понятия, объемы которых индивидуальны, делению не подлежат.
Главным законом структуры этой логической операции является требование - деление должно быть соразмерным. Это значит, что объем делимого понятия должен быть равен сумме объемов всех членов деления. Выполнение этого требования на практике не так просто, как может показаться, и предполагает основательные знания того предмета, той предметной области, которую отражает делимое понятие. Знание логических требований к этой операции не освобождает человека от необходимости знать и сам предмет (предметную область).
Уточняющими этот главный закон структуры данной операции являются следующие логические требования: деление должно производиться по единому, общему для членов деления признаку (основанию); признак деления должен быть четким, ясным, осознаваемым; члены деления должны исключать друг друга; деление должно быть полным, непрерывным, без скачков и пропусков.
Как правило, признаком (основанием) деления выступает существенный признак, но возможны и случаи, когда таким основанием деления выступает и несущественный, даже случайный признак (при недостаточно глубоком исследовании предметной области). Так было в классификации растительных видов К. Линнея, когда признаком деления выступало количество тычинок в цветке растений. Деление же понятия "треугольник" на "остроугольные", "прямоугольные" и "тупоугольные" осуществляется по существенному признаку остроты угла, видоизменение которого и отличает один член деления от другого, члены деления при этом исключают друг друга, а совокупный объем их равен объему исходного, делимого понятия, т.е. в делении нет пропусков, оно полное деление.
В зависимости от основания деления различают три вида данной логической операции: деление по видоизменению признака, дихотомическое деление и наиболее важный в науке вид деления — классификация (кодификация, систематизация, тарификация, стратификация, типология и пр.). Деление по видоизменению признака мы уже рассмотрели.
Дихотомия, или дихотомическое деление, — это деление любой предметной области, любого объема (множества, класса) всего лишь на два члена деления. А мы знаем из отношений между понятиями, что всю предметную область, весь ее объем исчерпывают только противоречащие (взаимодополняющие) понятия, поэтому дихотомия — это и есть деление на противоречащие члены деления, на два взаимоисключающие друг друга понятия. Например, мир природы можно делить на органический и неорганический. Общий объем этих двух понятий соответствует объему делимого понятия, так что дихотомия никогда не нарушает главного закона этой операции: она всегда соразмерна. Дихотомически делить можно по разным признакам. Тот же мир природы мы можем делить на живой и не-живой, на животный и не-животный, растительный и не-растительный, на молекулярный и не-молекулярный и т.п. Если строго выдерживать деление на противоречащие понятия, то ошибиться невозможно, но ошибки возможны при делении на противоположные понятия. Так, деля понятие "дерево" на "хвойное" и "не-хвойное", или "лиственное" и "не-лиственное" мы делим дихотомически, правильно; деля же это понятие на "хвойное" и "лиственное", т.е. тоже казалось бы дихотомически, мы не застраховано от ошибок, так как противоположные понятия не исчерпывают всю предметную область.
Классификация - настолько сложная по своей структуре операция, что ее вправе рассматривать не просто как особый вид деления, а и как самостоятельный вид научного исследования, как довольно проблематичную задачу по систематизации, упорядочивания предметной области. Классическим вариантом классификации по существенному признаку, классификации, отражающей закономерные связи в определенной предметной области, является система химических элементов Д.И. Менделеева. Однако, достичь такого совершенства в других предметных областях не всегда удается, например, при классификации наук. (См.: Кедров Б.М. Классификация наук. М., 1961).
Так как логическая операция деления лежит в основе всякой классификации, то и определяется она как такое распределение объема (множества, предметной области и пр.) на составляющие его виды (группы, классы и пр.) по единому основанию (признаку деления), при котором каждый вид занимает строго определенное место в системе других и обладает в зависимости от этого места определенными свойствами. Классификация, таким образом, не только распределяет, упорядочивает предметную область, но и устанавливает некоторые свойства видов этой предметной области, и поэтому выполняет роль не только систематизирующую, но и прогностическую, предсказательную, она есть вид опережающего отражения действительности, опережающего познания. Зачастую классификации выступают завершающим моментом научного исследования различных предметных областей - это и классификация (систематизация) растительных и животных видов, химических элементов, наук, правовых норм и пр.
Классификации подразделяются на искусственные (по несущественному признаку) и естественные (по существенному признаку). Выделяют также научные и ненаучные классификации и т.п.
Определение понятия есть логическая операция, раскрывающая содержание понятия, т.е. это перечисление тех существенных и отличительных признаков того или иного предмета (объекта), которые отражаются мыслью (определяемым понятием) о нем. Конечно, эти признаки являются и общими, но поскольку общность отражается объемом, то она не входит в содержание понятия. Поскольку существенных признаков, как правило, не так уж и много, то определения в большинстве своем лаконичны и эта их краткость является большим достоинством, потому что определения, раскрывая главное, легко запоминаются, воспроизводятся и ими удобно пользоваться.
Как логическая операция, как нечто целое, определение состоит из двух элементов: определяемого понятия, называемого дефиниендум и сокращенно записываемого dfd., и определяющих понятий, называемых дефиниенс и сокращенно записываемых dfn. Определяющие - это те понятия, с помощью которых раскрывается содержание определяемого. Законом связи этих двух элементов определения, законом структуры данной операции является требование логики, аналогичное требованию к делению, - определение должно быть соразмерным. Этот основной закон структуры данной логической операции записывается в виде формулы: Dfd=dfn. Требование его достаточно понятно, а конкретизацией и дополнением его выступают другие правила определения:
Определение не должно заключать в себе круга, т.е. определяемое понятие нельзя определять через само себя или через понятия, которые, в свою очередь, определяются с помощью определяемого понятия. Простейшим видом "круга" в определении выступает тавтология: то же, через то же. Например: человек есть человек; бизнес есть бизнес; масло есть масляное; окончание - это то, что стоит в конце; этого не может быть, потому что этого быть не может и т.п. Несколько сложнее тавтологии - определение через понятие, которое в свою очередь определяется через исходное: комичное то, что смешно, а смешное то, что комично; вращение есть движение вокруг оси, ось же есть прямая, вокруг которой происходит вращение; это правда, потому что это - истина, а истинно это потому, что правильно. Когда же подобный круг опосредуется не одним, а несколькими звеньями, то его «закругленность» делается менее заметной и узнаваемой, и ее неподготовленный человек, возможно, и не обнаружит. Например: человек есть разумное существо, потому что он мыслит; мыслит же тот, кто способен рассуждать; а рассуждает человек, потому что наделен разумом, следовательно, человек разумен. Или: логика - наука о правильном мышлении; правильное мышление - мышление по логическим правилам, поэтому правильное мышление - логичное мышление, а раз оно логичное мышление, то, значит, научное мышление, поскольку логика есть наука и т.п.
Именно поэтому в логике формулируется и такое правило - определение должно быть ясным, четким, свободным от двусмысленности, туманности и противоречивости; определение должно быть лаконичным. Запутанные определения не выполняют своей основной роли, они не раскрывают в краткой форме содержания определяемого понятия, их усложненные формулировки трудно запомнить и ими поэтому сложно пользоваться: «драка есть такое состояние, субъекты которого, выходя за рамки границ правовой объективности, совершают неправомерные вторжения в область охраняемых государством объективных прав личности, нарушая, тем самым, или стремясь нарушить целость физических покровов личности многократным нарушением таковых прав».
Своеобразным кругом в определении можно рассматривать и случай, когда определяемое (неизвестное) определяется через неизвестное: олигоцен - третья эпоха палеогена; сепулькарии - объекты, служащие для сепуления; туляремия - инфекционное заболевание септицемического типа, возбудителем которого является бацилюс туляренце.
Наконец, последнее правило-пожелание: определение, по возможности, не должно быть отрицательным, ибо отрицание не раскрывает сущности, не перечисляет существенные признаки предмета, отражаемого определяемым понятием: эвкалипт - дерево, которое не растет в Английском парке Старого Петергофа. Сказать, что тот или иной человек не есть ученый, еще не значит перечислить те существенно-отличительные признаки его, которые входят в содержание единичного понятия (мысли) об этом человеке. Правда, полностью обойтись без отрицательных определений в науке невозможно, особенно при определении некоторых принципиальных положений, некоторых аксиом (точка - то, что не имеет частей) и пр.
Определения в науке выступают обычно итогом исследования того или иного предмета, той или иной предметной области, являясь лаконичной, удобной для употребления формулировкой сущности исследуемого, хотя подлинным определением предмета (предметной области), конечно же, выступает вся научная теория, учение о нем. Если определением в науках обычно завершается исследование, то изложение науки, наоборот, начинается с определения. В логике особенно. Учитывая специфичность ее предмета, который невозможно представить в наглядном виде, определение в логике и выполняет роль общей характеристики, как бы внешнего описания предмета мысли, предмета исследования, изложения, поэтому в логике всякое изложение обычно и начинается с определения.
Как логическая операция с понятием, определение по структуре своей и по способности раскрывать возможно полнее содержание того или иного понятия, подразделяется на явное и неявное. Явные определения, перечисляя существенные и отличительные признаки определяемого, раскрывая его сущность, подразделяются на: определение через ближайший род и видовое отличие (назовем его одним словом, термином - дефиниция), генетическое определение и номинальное. Слово "дефиниция" часто употребляется в самом широком смысле, как любое определение. Но, на наш взгляд, дефиниция есть более строгое определение, наиболее научно значимое, это определение через ближайший род и видовое отличие.
Дефиниция своим развернутым названием выделяет два этапа в своей структуре: первый — подведение определяемого понятия под ближайшее к нему родовое (не просто под любое с большим объемом, а обязательно - под ближайшее для него родовое), и второй этап — перечисление тех существенно-отличительных признаков, которые собственно и составляют специфику содержания определяемого понятия. Приводимое раннее определение логики как науки выдержано именно как дефиниция, как дефинитивное определение. Определяемое понятие «логика» подводилось под ближайшее к нему родовое «философская наука» и далее перечислялись его отличительные, т.е. видовые, специфические признаки.
Генетическое определение указывает способ формирования, возникновения или образования определяемого предмета. Такие определения хорошо знакомы многим еще со школьного курса геометрии. Например, окружность там определяется как замкнутая кривая на плоскости, образованная движением точки В отрезка АВ вокруг неподвижной точки А. В этом определении легко выделима та же структура, что и у дефиниции, потому что «замкнутая кривая» определенно выступает родовым понятием по отношению к определяемому, а описание способа формирования его есть как бы перечисление отличительных признаков определяемого предмета.
Номинальное определение, или определение имени, слова есть определение, которое направлено лишь на раскрытие смысла, значения, назначения и особенностей слова (имени, знака), не касаясь существенных признаков того предмета, который данным словом обозначен. Номинальными будет, таким образом, все статьи этимологических и толковых словарей, так как в них речь идет не о предметах, а о словах. Номинальным будет, например, следующее определение слова «лавсан»: это - слово, образованное сокращением названия «лаборатория высокомолекулярных соединений». При этом, данное определение ничего не говорит о сущности нового синтетического материала, полученного в этой лаборатории. Или, определяя слово "философия", говорим, что оно составлено из двух древнегреческих слов "филэо" - любовь и "софос" - мудрость, тоже, ведь, при этом не говорим о сущности данной науки, не раскрываем ее содержания. Определяя микроскоп как слово, которым называют инструмент наблюдения очень мелких предметов, мы тоже даем, скорее, номинальное определение. Номинальное - от средневекового термина ноумен, которым пользовались номиналисты, признававшие существование единичного, а все общее объявлявшие лишь словом, понятием. Разновидностей номинальных определений много, можно выделять номинальное определение синтаксического, семантического, знакового характера.
К неявным определениям относится довольно большая группа приемов, сходных с определением: остенсивное определение, или указание, описание, метафора, сравнение, гипербола, характеристика, операциональное определение, контекстуальное определение, определение через перечисление, определение через противоположность и некоторые другие. Поскольку многие из них не имеют прямого отношения к логике, это филологические особенности, то охарактеризуем лишь некоторые из них.
Указание — словесное сопровождение непосредственно воспринимаемой вещи (явления, процесса), на которую указывают пальцем. В логике этот прием называют «остенсивное определение», т.е, буквально - указание пальцем. Остенсивным определением обычно пользуются при ознакомлении ребенка с незнакомым ему предметом, или при общении с людьми, не владеющими языком общения, да и при изучении иностранных языков.
Описание — более подробная словесная характеристика того предмета, который наблюдается непосредственно, или словесное художественное изображение той или иной картины для представления ее другим, как это имеет место в художественной и иной литературе (например, описание Днепра у Гоголя).
Сравнение (различение), или метафора, — прием, используемый при сопоставлении двух или нескольких предметов (понятий), когда один из предметов более известен, чем другой. Например, совесть — это внутренний суд; дети — цветы жизни, экзаменационная сессия - период истребительных войн, мозг учащегося - поле сражения и пр. Литературно-художественная, да и научная, метафора это тоже сравнение: жизнь - сцена, а люди - актеры на ней и пр. Различение - тоже сравнение, только акцент здесь не на сходстве: отвага отличается от безрассудства тем, что направлена на благородное дело, а вот безрассудство может быть связано и с позерством, эгоистическими целями, неблаговидными поступками.
Характеристика — это более подробное описание предмета с выделением отличительного, характерного, а то и существенного признака (признаков) в предмете (явлении, процессе). Характеристика помимо описании предполагает и некоторое обобщение, стремление проникнуть в сущность через внешние признаки, через являющееся, поверхностное, что всем знакомо хотя бы по служебным и иным характеристикам.
Операциональное определение — определение действием, экспериментом, заключающееся в выполнении специальных правил, приемов, определенной последовательности. Кислота определяется, например, как такое вещество, которое окрашивает лакмусовую бумагу в красный цвет.
Контекстуальное определение - определение через текст, в котором определяемое явно не называется, а характеризуется, описывается косвенно, иносказательно.
Определение через перечисление предметов, входящих в объем определяемого понятия или тех, на которые распространяется определяемое понятие, используется довольно часто и особенно тогда, когда явного определения, раскрывающего сущность, дать не удается. Это, например, следующее юридическое определение понятия «близкие родственники»: это «родители (усыновители), дети, братья, сестры, а также дедушка и бабушка».
Определение через противоположность, через полярное отношение используется тогда, когда у понятия нет более широкого для него родового понятия. Так, известные из философии определения категорий «материя», «движение», «сознание», «пространство», «время», «случайность», «необходимость» и пр. являются определениями через противоположность, через отношение их к своей парной, но полярной им категории.
К приемам, сходным с определением можно отнести и так называемые определения через пример, схему, чертеж, таблицу и пр.
Глава 3.
СУЖДЕНИЕ
ОБЩАЯ ХАРАКТЕРИСТИКА СУЖДЕНИЯ
Форма мысли, представляющая собой логическую связь двух и более понятий, могущая быть истинной или ложной, называется суждением. Между понятиями,… Всякое суждение выразимо предложением, но не всякое предложение может выражать… Однако, признаки суждения и признаки предложения (знакового комплекса) не совпадают и не тождественны друг другу. Если…ЕГО СТРУКТУРА И ВИДЫ
Опираясь на уже известное определение простого суждения, категорическое суждение (суждение действительности) можно определить как такое, в котором… Как и любое суждение, простое категорическое суждение может быть истинным… Структура простого категорического суждения обычно представляется трехэлементной, т.е. такое суждение состоит из…ОТНОШЕНИЯ МЕЖДУ ПРОСТЫМИ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ
Между известными видами простых категорических суждений устанавливаются следующие отношения: противоречия (контрадикторности), противоположности… Отношение противоречия (контрадикторности) устанавливается между суждениями,… Отношение противоположности (контрарности, противности) устанавливается между общими суждениями, но разными по…ОПЕРАЦИИ С ПРОСТЫМИ КАТЕГОРИЧЕСКИМИ СУЖДЕНИЯМИ
Накопленное богатство знаний об этой форме мысли послужит нам базой для определенных действий, операций с суждением. Действия эти совершаются с суждением как целостным единством составных его элементов и не меняют исходную истинностную характеристику этого суждения; действия также не должны нарушать другие требования и законы логики. Операции - это, условно говоря, "практические" интеллектуальные действия с данной формой мысли, реализующие накопленные о ней знания. К логическим операциям с простыми категорическими суждениями относятся отрицание, обращение, превращение и противопоставление. Помимо этих операций к действию с суждениями следует отнести и преобразования по логическому квадрату, которые позволяют, исходя из одного суждения, получить три остальных с определенными истинностными характеристиками. Некоторые авторы рассматривают эти действия как "непосредственные" умозаключения, т.е. как выводы из одного исходного суждения (посылки); однако, данная операция не дает нового суждения, которое бы несло и новое содержание, что свойственно умозаключению, а выступает лишь действием по видоизменению элементов исходного суждения.
Отрицание суждения связано, естественно, с отрицательной частицей "не" и прежде всего понимается как отрицание главного элемента этой мыслительной структуры - связки, как замена утвердительной на отрицательную и наоборот, т.е. отрицать можно не только утвердительное суждение, но и отрицательное. Такое понимание отрицания суждения можно считать главным. Этим действием истинное исходное суждение превращается в ложное, а ложное - в истинное. Однако, отрицать исходное суждение можно по-разному. Можно отрицать суждение через отрицание квантора, через отрицание субъекта, через отрицание предиката, через отрицание нескольких элементов суждения сразу. Не всегда подобные действия (в силу сложности структуры суждения) могут гарантировать сохранение истинности исходного суждения. В традиционном курсе логики отрицание суждения специально и обстоятельно не рассматривается. Здесь много сложностей, в частности: так как суждение "Не все S есть Р" тождественно частноутвердительному суждению "Некоторые S есть Р", то получается, что даже подчиненное суждение порой может выступать отрицанием общего: общеутвердительное суждение "Все S есть Р" можно отрицать частноутвердительным же суждением "Только некоторые S есть Р", или "Не верно, что все S есть Р". Боле разработанной в логике является операция отрицания суждения под названием превращение.
Превращение представляет собой операцию, связанную с изменением качества исходного суждения (т.е. связки), при этом предикат выводного суждения должен противоречить предикату исходного. Таким образом, утвердительное суждение превращается в отрицательное, а отрицательное в утвердительное. Превращение есть операция с использованием в сущности двойного отрицания: первое отрицание — замена связки на противоположную, второе — замена предиката исходного суждения противоречащим ему понятием. По формуле это будет выглядеть:
S есть Р или S не есть Р
S не есть не-P S есть не-Р
Общеутвердительное суждение превращается в общеотрицательное. В смысловом отношении оба эти суждения одинаковы, но логический вид их различен:
Все студенты есть учащиеся (А) Все S есть Р
Все студенты не есть не-учащиеся [Е). Все S не есть не-P
Общеотрицательное суждение превращается и общеутвердительное:
Все рыбы не есть млекопитающиеся (Е) Все S не есть Р
Все рыбы есть не-млекопитающиеся (А) Все S есть не-P
Частноутвердительное суждение превращается в частноотрицательное:
Часть студентов есть спортсмены (I) Некоторые S есть Р
Часть студентов не есть не-спортсмены (О). Некоторые S не есть не-Р
Частноотрицательное суждение превращается в частноутвердительное:
Некоторые книги не есть интересные (О) Некоторые S не есть Р
Некоторые книги есть не-интересные (I). Некоторые S есть не-Р.
Итоговая таблица:
А превращается в Е
Е превращается в А
I превращается в О
О превращается в I
Обращение — логическая операция с простым категорическим суждением, заключающаяся в перестановке местами субъекта и предиката исходного суждения. Таким образом, субъект исходного суждения становится предикатом выводного суждения, а предикат исходного — субъектом выводного. При этом качество суждения и объем входящих в него понятий не меняются. Обращение — операция довольно простая, в символах выполняется почти механически. Если исходное суждение имеет вид «S есть Р», то выводное, получаемое в результате обращения, будет «Р есть S»:
Такая обобщенная форма записи обращения не учитывает особенностей видов простого категорического суждения, а тем самым и объемных характеристик, входящих в суждение понятий. С учетом же их, общеутвердительное суждение (А) обращается, как правило, в частноутвердительное (I), ибо предикат в утвердительном суждении, как известно, нераспределен. А согласно требованию логики, соответственно закону тождества, понятие (иначе говоря — термин: этим словом в логике называют любое понятие, входящее в суждение), не распределенное в исходном суждении, не может быть распределено в выводном. В тех исключительных случаях, когда объемы предиката и субъекта общеутвердительного суждения тождественны между собой, обращение может быть прямым, без ограничения, т.е. общеутвердительное суждение обратимо в общеутвердительное: «Все квадраты есть ромбы с прямыми углами» обращается в общеутвердительное суждение «Все ромбы с прямыми углами есть квадраты». В большинстве же случаев общеутвердительное суждение обращается в частноутвердительное:
«Все студенты — учащиеся»
«Некоторые учащиеся — студенты».
Общеотрицательное суждение (Е) в силу того, что в нем и субъект и предикат всегда распределены, будет обращаться прямо, без ограничения в общеотрицательное: Ни один круг не есть треугольник (Е)
Ни один треугольник не есть круг (Е)
Частноутвердительное суждение обращается в частноутвердительное же, что вполне понятно, ибо в этом суждении и субъект и предикат нераспределены. Такое обращение называется тоже прямым:
Некоторые спортсмены — студенты (I)
Некоторые студенты — спортсмены (I)
Тот исключительный для частноутвердительного суждения случай, когда объем предиката его полностью входит в объем субъекта этого же суждения, т.е. когда предикат есть вид по отношению к субъекту (роду), и поэтому распределен, в этом случае частноутвердительное суждение обращается в общеутвердительное. Этом случай называется обращением с обобщением. Выполнить эту операцию можно, лишь зная истинность конкретного по содержанию суждения:
Некоторые учащиеся - студенты (I)
Все студенты - учащиеся (А)
Что касается частноотрицательного суждения, то оно, как общепринято в логике, считается не поддающимся обращению. И это достаточно очевидно, ибо формула частноотрицательного суждения «Некоторые S не есть Р» не позволяет однозначно уточнить соотношение его субъекта и предиката. Между тем, оно допускает три случая, в круговых схемах выразимых так:
Некоторые S не есть Р
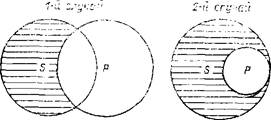
Какой именно вариант соотношения субъекта и предиката имеется в виду, из формулы частноотрицательного суждения не ясно. Снять эту неопределенность возможно лишь зная конкретное содержание исходного суждения, но логика конкретным содержанием не занимается, поэтому она отказывается от обращения такого суждения и это записано в большинстве учебников по логике.
Однако, как нам представляется, частноотрицательное суждение можно обращать и во всех отмеченных случаях. Даже более того, для обращения частноотрицательного суждения не обязательно и знать конкретное содержание его: во всех случаях результатом обращения будет общеотрицательное суждение, т.е. возможно обращение с обобщением, хотя для первого случая более естественным является обращение прямое. Например:
Некоторые студенты не есть спортсмены (О)
Некоторые спортсмены не есть студенты (О).
Но это же суждение может обращаться и в общеотрицательное. Обоснование таково: так как во всех отрицательных суждениях предикат всегда распределен, то он при перестановке его на место субъекта выводного суждения может браться во всем своем объеме:
Некоторые студенты не есть спортсмены (О)
Все спортсмены не есть эти "некоторые студенты" (Е}
И во 2-м случае частноотрицательное суждение, опять же, обращается в общеотрицательное:
Некоторые учащиеся не есть студенты (О)
Все студенты не сеть эти «некоторые учащиеся» [Е)
Так же и в 3-м случае обращение частноотрицательного суждения возможно с обобщением, например:
Некоторые студенты не есть птицы (О)
Все птицы не есть эти ''некоторые студенты" (Е)
Хотя в этом последнем случае, как мы знаем из действительности, не только "некоторые студенты", но все они не есть птицы, однако, по принципиальным для логики соображениям, мы не меняем объем исходного понятия, так как термин, не распределенный в исходном суждении, не может быть распределенным в выводном.
Итоговая таблица для операции обращения следующая:
А обращается в I (А)
Е обращается в Е
I обращается в I (А)
О не обращается
Такова общепринятая таблица, но так как мы отстаиваем иную точку зрения, а именно, что частноотрицательное суждение тоже обращается, то добавляем: О обращается в Е.
Последняя логическая операция — противопоставление — есть действие, в результате которого меняется качество исходного суждения (связка меняется на противную), меняются местами субъект и предикат его, и при этом субъект (или предикат) выводного суждения должен противоречить предикату (или субъекту) исходного. Эта операция может рассматриваться и как самостоятельная, и как комбинированная из двух предшествующих.
Противопоставленное исходному суждение мы можем получить двумя способами. Первый способ: вначале исходное суждение (Все S есть Р) превращается (Все S не есть не-Р), а потом превращенное обращается (Все не-Р не есть S). В данном случае, конечное суждение будет противопоставленным предикату исходного суждения. Второй способ: вначале исходное суждение (Все S есть Р) обращается (Некоторые P есть S), а потом обращенное превращается (Некоторые Р не есть не-S). Здесь конечное суждение будет противопоставленным субъекту исходного суждения. Такой результат получить применяя операцию противопоставления сразу, руководствуясь ее определением, значительно сложнее, особенно в связи с получением из общего суждения частного. Например:
Все S есть Р
Некоторые Р не есть не-S.
Поэтому, более простой и надежный вариант - поэтапное противопоставление, последовательное выполнение превращения и обращения в одном случае, и наоборот - в другом.
Общеутвердительное суждение противопоставляется в общеотрицательное (противопоставление предикату), и в частноотрицательное (противопоставление субъекту). Например:
Все студенты — учащиеся Все студенты — учащиеся
Все не-учащиеся не есть студенты. Некоторые учащиеся не есть не-студенты.
Общеотрицательное суждение противопоставляется в частноутвердительное (противопоставление предикату), и в общеутвердительное (противопоставление субъекту). Например:
Все студенты не есть птицы Все студенты не есть птицы
Некоторые не-птицы есть студенты. Все птицы есть не-студенты
Частноутвердительное суждение не противопоставляется предикату, потому что уже первая процедура - превращение частноутвердительного исходного суждения - даст нам частноотрицательное, а оно, как известно, не обращается; противопоставление, тем самым, не завершается. Субъекту же частноутвердительное суждение противопоставляется. Выполним эту операцию поэтапно:
Некоторые студенты - спортсмены
Некоторые спортсмены - студенты
Некоторые спортсмены не есть не-студенты
Частноотрицательное суждение, наоборот, противопоставляется предикату частноутвердительным суждением, и не противопоставляется субъекту, поскольку чрстноотрицательное суждение не обращается. Например:
Некоторые студенты не есть спортсмены
Некоторые студенты есть не-спортсмены
Некоторые не-спортсмены есть студенты
Продолжая же реализовывать нашу особую точку зрения на обращение частноотрицательного суждения, следует отметить, что с этой точки зрения возможны как противопоставление частноутвердительного суждения предикату, так и противопоставление частноотрицательного суждения субъекту. При противопоставлении частноутвердительного суждения предикату получаем общеотрицательное суждение, а при противопоставлении частноотрицательного субъекту - общеутвердительное суждение. Например:
Некоторые студенты - спортсмены
Некоторые студенты не есть не-спортсмены
Все не-спортсмены не есть эти "некоторые студенты"
Некоторые студенты не есть спортсмены
Все спортсмены не есть эти "некоторые студенты"
Все спортсмены есть не эти "некоторые студенты"
Сводная таблица операций
С простыми категорическими суждениями
МОДАЛЬНЫЕ СУЖДЕНИЯ
Мы не будем говорить о выделяемой логиками модальности в широком смысле (об этом можно прочесть в специальной литературе). Будем рассматривать лишь… Необходимость безотносительна ко времени (прошлому, настоящему и будущему) и… Действительность соответствует настоящему времени и подчеркивается связками "есть", "не есть",…ПРОСТОЙ КАТЕГОРИЧЕСКИЙ СИЛЛОГИЗМ И ЕГО СТРУКТУРА
В простом категорическом силлогизме символом "S", как и обычно, обозначается субъект вывода и соответствующее ему понятие в посылке. Это -… Все студенты - учащиеся Некоторые спортсмены - студентыВИДЫ ПРОСТОГО КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА
В зависимости от занимаемого средним термином места в посылках (а он может занимать любое место, то ли субъекта в обеих посылках, то ли предиката в… Умозаключение, в посылках которого средний термин занимает место субъекта в… Умозаключение, средний термин которого занимает место предиката в обеих посылках, называется второй фигурой простого…ОТНОШЕНИЯ МЕЖДУ ВИДАМИ КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА
Отношения между видами категорического силлогизма есть в сущности отношения между фигурами и модусами их. Сопоставляя модусы фигур, легко… Все остальные фигуры и их модусы находятся в зависимости от первой фигуры и ее… При внешнем сопоставлении фигур легко обнаружить, что по конфигурации первая и четвертая фигуры противоположны друг…ОПЕРАЦИИ С ВИДАМИ ПРОСТОГО КАТЕГОРИЧЕСКОГО СИЛЛОГИЗМА
К операциям с данной формой мысли следует отнести то, что частично уже было затронуто, а именно - сведение модусов II-IV фигур к модусам первой фигуры, поскольку она занимает особое привилегированное положение в сравнении с остальными. Ее место определяет и старшинство модусов первой фигуры, подчиняющее их положение по отношению к другим модусам. Как же совершается сведение модусов в каждом отдельном случае?
Конкретный прием сведения модусов закодирован в их названии. Если в названии модусов II-IV фигур встречается согласная "m", то эти модусы сводимы путем простой перестановки посылок местами. Это достаточно очевидно для четвертой фигуры, но менее - для третьей и второй. В них перестановка посылок сопровождается еще и другими действиями, о которых напоминают другие согласные в названии модусов. Наличие в названии модусов согласной "p" говорит о том, что суждение перед этой согласной необходимо обратить, а при наличии в названии модусов согласной "s" - что суждения перед данной согласной обращаются прямо, без ограничения. Так как обращение без ограничения возможно либо с общеотрицательным суждением, в котором и субъект и предикат всегда распределены, либо с частноутвердительным суждением, в котором и субъект и предикат не распределены, то можно быть уверенным, что перед согласной "s" всегда будет или общеотрицательное (Е), или частноутвердительное (I) суждение.
Суммируем сказанное: модусы II-IV фигур, названия которых начинаются соответствующими согласными, сводимы к модусам первой фигуры с такими же заглавными буквами, кроме двух - модуса Baroco и Bocardo, о чем свидетельствует согласная "с" в их названии; наличие в названии модусов согласной "m" говорит о необходимости при сведении поменять посылки местами; наличие согласной "р" - что суждения перед нею обращаются; а наличие согласной "s" - что они обращаются без ограничения. Остальные согласные - для благозвучия.
Возьмем, например, модус четвертой фигуры Bramantip, название которого говорит, что он сводим к модусу Barbara. Раз в названии модуса встречаются две согласные, имеющие определенное процессуальное значение, - m и р, то выполняя последовательно соответствующие действия, именно - вначале меняем посылки местами, а потом обращаем выводное суждение, - в итоге и получаем модус Barbara первой фигуры:
Все мои друзья - студенты (А) P --- M Это IV фигура.
Все студенты - учащиеся (А) M --- S
Некоторые учащиеся - мои друзья (I) S --- P
Меняем посылки местами и одновременно обращаем вывод:
Все студенты - учащиеся (А)
Все мои друзья - студенты (А)
Все мои друзья - учащиеся (А)
В итоге получаем модус Barbara первой фигуры. Понятно, что по четвертой фигуре вывод не мог быть общим суждением, так как субъект вывода является предикатом утвердительной меньшей посылки, а предикат утвердительных посылок, как правило, нераспределен; зато по первой фигуре вывод, естественно, общий, поскольку субъект вывода является субъектом общеутвердительной меньшей посылки.
Модусы Сеsаrе, Саmеstres, Саmеnеs сводимы к модусу первой фигуры Сеlаrеnt. Например:
Все коровы не есть птицы (Е) P --- M
Все воробьи - птицы (А)S --- M
Все воробьи не есть коровы (Е) S --- P
Это модус Cesare второй фигуры. Согласная s в его названии показывает, что сведение к модусу Celarent первой фигуры возможно всего лишь одним действием - прямым обращением большей общеотрицательной посылки, т.е. суждения перед согласной s:
Все птицы не есть коровы (Е) М --- Р
Все воробьи - птицы (А)S --- M
Все воробьи не есть коровы (Е) S --- P
Возьмем другой модус:
Все тигры - позвоночные (A) P --- M
Все насекомые не есть позвоночные (E) S --- M
Все насекомые не есть тигры (E) S --- P
Это модус Camestres II фигуры, в названии которого присутствуют две значащие для нашей операции согласные - m и s, при этом s в названии модуса встречается дважды. Данный модус простым обращением большей посылки (так как она общеутвердительное суждение и обращается только в частноутвердительное суждение, не могущее быть большей посылкой первой фигуры) превратить в модус I фигуры невозможно. Поэтому, вначале обратим общеотрицательную меньшую посылку (она обращается прямо), потом поменяем, согласно m, посылки местами и, наконец, обратим тоже прямо общеотрицательный вывод. В итоге получаем модус Celarent первой фигуры:
Все позвоночные не есть насекомые (E) M --- P
Все тигры - позвоночные (A)S --- M
Все тигры не есть насекомые (E) S --- P
Модус Camenes четвертой фигуры сводим к модусу Celarent простой перестановкой посылок местами и прямым обращением общеотрицательного вывода. Например, исходный модус IV фигуры:
Все птицы имеют клюв (А) P --- M
Все имеющие клюв не являются насекомыми (Е)M --- S
Все насекомые не являются птицами (Е) S --- P
Выполняем зашифрованные в названии модуса действия:
Все имеющие клюв не являются насекомыми (Е) М --- Р
Все птицы имеют клюв (А)S --- М
Все птицы не являются насекомыми (Е) S --- Р
Модусы Dаrарti, Disamis, Datisi, Dimaris сводимы к модусу Dаrii. Например, модус Darapti третьей фигуры:
Все киты - млекопитающиеся (A) M --- P
Все киты живут в воде (А) M --- S
Некоторые живущие в воде - млекопитающиеся (I) S --- P
Этот модус сводим всего лишь обращением меньшей посылки, являющейся общеутвердительным суждением, обращаемым с ограничением в частноутвердительное. В итоге получаем модус Darii первой фигуры:
Все киты - млекопитающиеся (A) M --- P
Некоторые, живущие в воде, - киты (I) S --- M
Некоторые, живущие в воде, - млекопитающиеся (I) S --- P
Модусы Festino, Felapton, Ferison, Fesapo, Fresison сводимы к модусу Ferio. Например, Felapton третьей фигуры:
Ни один тигр не есть травоядное (Е) М --- Р
Все тигры - хищники (А)М --- S
Некоторые хищники не есть травоядные (О) S --- P
Данный модус сводится обращением меньшей посылки, а так как она общеутвердительное суждение, то обращается в частноутвердительное, и в итоге получается модус Ferio первой фигуры:
Ни один тигр не есть травоядное (E) M --- P
Некоторые хищники - тигры (I) S --- M
Некоторые хищники не есть травоядные (О) S --- P
СОКРАЩЕННЫЕ, СЛОЖНЫЕ И СЛОЖНОСОКРАЩЕННЫЕ КАТЕГОРИЧЕСКИЕ СИЛЛОГИЗМЫ
Своеобразными видами простого категорического силлогизма выступают сокращенные, сложные и сложносокращенные силлогизмы. Структура их в целом ясна из… Естественно, что полными силлогизмами как в повседневной, так и научной… В логике выделяют четыре вида сокращенных, сложных и сложносокращенных силлогизмов, это - энтимема, эпихейрема,…УСЛОВНЫЕ И РАЗДЕЛИТЕЛЬНЫЕ СИЛЛОГИЗМЫ
К числу силлогистических умозаключений относят умозаключения из условных, разделительных суждений, их сочетаний с простыми категорическими суждениями и между собой. Таким образом, можно говорить об условном, разделительном, условно-категорическом, разделительно-категорическом и условно-разделительном силлогизмах (умозаключениях).
Силлогизм, в котором хотя бы одна из посылок — суждение условное, является условным силлогизмом. Когда в умозаключении обе посылки суждения условные, тогда силлогизм называется чисто условным. Когда одна из посылок — суждение условное, а другая — суждение категорическое, тогда силлогизм называется условно-категорическим. Когда же одна из посылок — суждение условное, а другая — суждение разделительное, тогда силлогизм называется условно-разделительным.
Умозаключение, в котором хотя бы одна из посылок — суждение разделительное, называется разделительным силлогизмом. Аналогично условному и здесь выделяют чисто разделительное умозаключение, когда обе посылки — разделительные суждения; разделительно-категорическое умозаключение и, наконец, разделительно-условное, которое, собственно, то же самое, что и условно-разделительное. Структуру этих умозаключений определяют входящие в них посылки, и эту структуру следует рассмотреть более обстоятельно в каждом отдельном случае.
Чисто условный силлогизм состоит из двух условных суждений, структура каждого из которых уже известна: условное суждение состоит из основания, следствия и логического союза между ними. Хотя структуру условного суждения можно представлять в субъектно-предикатной записи, например: "Если S есть Р, то S1 есть Р1", но такая запись лишь усложняет анализ, поэтому будем пользоваться сокращенной записью этих суждений, сохраняющих и даже выделяющих главные структурные элементы сложных суждений - логический союз и отдельные простые суждения. Обозначив входящие в условное суждение простые суждения отдельными символами, получим формулу условного суждения: Если В, то С. Используя символ и для логического союза, получаем еще более сокращенную запись: «В --> C»
Пользуясь этой сокращенной записью, чисто условный силлогизм можно представить такой схемой:
Если В, то С В -->С
Если С, то ДС -->Д
Если В, то Д В -->Д
Легко заметить, что роль среднего термина в чисто условном силлогизме выполняет простое суждение, являющееся в первой посылке следствием, а во второй посылке основанием этого условного суждения. Такая структура напоминает собой четвертую фигуру категорического силлогизма, однако разница существенна: там средний термин — общее для посылок понятие, здесь — общее простое суждение. Например:
Если через проводник пропустить ток, то он нагреется
Если проводник нагреется, то он расширится
Если через проводник пропустить ток, то проводник расширится.
Чисто условный силлогизм имеет единственный вариант своей структуры и простотой своей напоминает собой модус Barbara первой фигуры категорического силлогизма и особенно в аристотелевской манере его записи:
А сказывается обо всех Б
Б сказывается обо всех В
А сказывается обо всех В
Это не случайно, потому что данная структура отражает общую, присущую количественным (объемным), временным, пространственным, причинно-следственным и другим отношениям закономерность: величины (предметы, объемы и пр.), находящиеся в определенном отношении к третьей, находятся в том же определенном отношении и между собой.
Условно-категорический силлогизм состоит из условной (будем считать ее большей, ибо она сложное суждение) и категорической (будем называть ее меньшей, ибо она - простое суждение) посылок. Структура этого умозаключения допускает четыре разновидности, четыре ее модуса, определяемых законами связи элементов в условном суждении. Этих законов два: при истинности основания условного суждения - следствие его будет обязательно истинным, и наоборот, при ложности следствия условного суждения - основание его будет обязательно ложным. Если в условно-категорическом умозаключении от утверждения (констатации, признания истинности) основания условного суждения в меньшей категорической посылке переходит в заключении этого силлогизма к утверждению следствия условного суждения, то такой вывод правилен, он соответствует нормам логики:
Если В, то С В -->С
В В
С С
Это умозаключение представляет собой утверждающий модус (modus роnеns) условно-категорического силлогизма.
Если в условно-категорическом силлогизме мысль переходит от отрицания следствия (признания, констатации его несоответствия действительности, т.е. ложности) условного суждения в меньшей посылке, то необходимо в заключении силлогизма отрицать само основание условного суждения:
Если В, то С В -->С
не-Сне-С
Не-В не-В
Это умозаключение представляет собой отрицающий модус (modus tollеns) условно-категорического силлогизма.
Оба модуса — утверждающий и отрицающий — гарантируют необходимость и истинность вывода при истинности посылок. Два остальных модуса этого вида силлогизма не дают необходимо истинного вывода, так как их структурные особенности не соответствуют правилам, законам логики. Модусы эти называются неправильными, неправомочными, проблематичными, правдоподобными. Они дают знание, которое в одном случае (что определяется содержанием посылок) может быть ложным, в другом истинным. Формулы этих модусов записываются так:
В -->С В -->С
не-В С
(возможно, не-С) (возможно, В)
? ?
Чисто разделительный силлогизм составляют разделительные посылки, например:
Четырехугольники суть равносторонние или они неравносторонние
Равносторонние четырехугольники есть квадраты или ромбы
Четырехугольники есть неравносторонние, или квадраты, или ромбы
Символически это можно записать так:
S есть Р или S есть Р1
Р есть Р2 или Р3
S есть Р1 или Р2 или Р3
Умозаключение, в котором на месте большей посылки — суждение разделительное, а на месте меньшей посылки — суждение категорическое, называется разделительно-категорический силлогизм. Как и условно-категорический силлогизм, разделительно-категорический тоже имеет всего два правильных модуса: утверждающе-отрицающий, или роnеndо-tоllеns, и отрицающе-утверждающий, или tоllеndо-роnеns. Например:
Деревья у нас либо лиственные, либо хвойные
Данное наше дерево - хвойное
Данное дерево - не лиственное
Другой пример:
Деревья у нас либо лиственные, либо хвойные
Данное наше дерево - не хвойное
Данное дерево - лиственное
В этих разделительно-категорических силлогизмах меньшая посылка в первом случае утвердительное суждение, а вывод отрицателен, во втором - отрицательная, но вывод положителен. Соответственно, эти модусы и называются - утверждающе-отрицающий (роnеndо-tollеns) и отрицающе-утверждающий (tollendo-ponens).
В разделительно-категорическом силлогизме можно выделить четыре их разновидности, или модуса:
В v С В v С В v С В v С
В не-В С не-С
не-С С не-В В
Однако, легко обнаружить, что здесь фактически лишь два их вида, поскольку каждый из них имеет свою пару. Поэтому, обычно и говорится, что разделительно-категорический силлогизм имеет только два правильных модуса: утверждающе-отрицающий и отрицающе-утверждающий.
В использовании условных и разделительных умозаключении следует соблюдать не только требования к силлогизмам, но и все требования логики к сложным суждениям, входящим в это умозаключение. Условное суждение должно отражать естественные, причинно-следственные зависимости, ибо только в этом случае вывод по условно-категорическому силлогизму будет правильным. В случае же когда основание и следствие условного суждения не соответствуют своему структурному значению (когда их, например, поменяют местами), в силлогизме, где участвует условное суждение, вывод с необходимостью следовать не может: когда человек болен лихорадкой, то у него высокая температура, но когда у него высокая температура, это еще не значит, что он болен лихорадкой.
И в разделительном силлогизме правильность вывода будет гарантирована лишь тогда, когда в разделительной посылке будут перечислены все члены деления (деление должно быть полным), и при этом члены деления должны исключать друг друга, что следует из уже известного правила деления.
Наиболее сложным из рассматриваемых является условно-разделительный силлогизм. Он составляется из условной (будем считать ее большей) и разделительной (будем считать ее меньшей) посылок. Обычно условно-разделительные умозаключения называют лемматическими (от древнегреческого lemma - предположение). Структурно они подразделяются на дилеммы, трилеммы и полилеммы.
Дилемма — условно-разделительный силлогизм с двумя взаимоисключающими выводами, альтернативами. Смысл дилеммы заключается в необходимости выбора одного из двух возможных, как правило, взаимоисключающих друг друга решений. Различают два вида, или модуса, дилеммы: утверждающий и отрицающий. Утверждающий иначе называют конструктивной дилеммой, отрицающий модус — деструктивной дилеммой.
В конструктивной (утверждающей) дилемме условная (большая) посылка устанавливает два возможных основания и два вытекающих из них следствия. В разделительной (меньшей) посылке говорится о возможности только одного из двух оснований. В заключении же утверждается возможность только одного из двух следствий. Например:
Если Иванов - дисциплинированный студент, то он регулярно посещает учебные занятия; если же Иванов - недисциплинированный студент, то он часто пропускает учебные занятия.
Иванов либо дисциплинированный студент, либо недисциплинированный.
Иванов либо регулярно посещает учебные занятия, либо часто пропускает их.
В виде схемы этот модус структурно представляется более наглядно:
Если В то С; если Д, то К
Либо В, либо Д
Либо С, либо К
В логике выделяют и упрощенный вариант конструктивной дилеммы, когда в условной посылке из двух разных оснований вытекает одно и то же следствие:
Если В, то С; если Д, то С
Либо В, либо Д
С
Главная особенность этих рассуждений заключается в переходе мысли от основания к следствию условного суждения, т.е. в соблюдении того закона, который определяет структурные зависимости элементов условного суждения.
В деструктивной (отрицающей) дилемме большая условная посылка устанавливает два возможных следствия из двух оснований. В разделительной меньшей посылке отрицаются оба возможных следствия. В заключении необходимо отрицаются и сами основания:
Если В, то С; если Д, то К
Либоне-С, либо не-К
Не-В либо не-Д
В логике чаще рассматривается упрощенный вариант деструктивной дилеммы. В ней в большей условной посылке два возможных следствия устанавливаются из одного и того же основания:
Если наш товарищ — студент химического факультета, то он либо студент очного отделения, либо студент вечернего отделения.
Наш товарищ или не студент очного отделения, или не студент вечернего отделения.
Наш товарищ не студент химического факультета.
Это рассуждение вполне может соответствует действительности, поскольку специфика этой специализации не допускает возможности заочного обучения.
В деструктивной дилемме срабатывает уже другой закон структуры условного суждения, а именно: ложность следствия условного суждения необходимо влечет за собой и ложность самого основания этого суждения:
Если В, то С или Д
Не-С или не-Д
Не-В
Условно-разделительные силлогизмы еще в древности пользовались большой популярностью и им соответствовали многие исторические и курьезные случаи. Известна дилемма, с которой скифы будто бы обращались к Александру Македонскому:
Если ты бог, то благодетельствуй людям, если ты человек, то не забывай о человечности
Но ты или бог, или человек
Сл.: Ты или благодетельствуй людям, или не забывай о человечности.
А известный из истории философии случай с Эватлом, учеником Протагора, который обязался заплатить учителю за обучение после первого же выигранного им в суде дела. Эватл в судах после учебы не участвовал и Протагор, чтобы получить с ученика плату за обучение, сам обратился в суд, сказав Эватлу:
Если я выиграю дело, то ты заплатишь мне по решению суда; если же я проиграю, то ты заплатишь мне по нашему договору
Но я или выиграю дело, или проиграю его
Следовательно, в любом случае ты должен будешь заплатить мне.
Казалось бы, выхода нет. Но не зря Эватл прошел курс обучения у столь авторитетного софиста. Он нашелся ответить учителю не менее убедительной дилеммой:
Если я выиграю дело, то не заплачу тебе по решению суда; если же проиграю дело, то не заплачу по нашему договору
Но я или выиграю дело, или проиграю
Следовательно, в любом случае я не заплачу.
Трилемма — условно-разделительный силлогизм с тремя взаимоисключающими выводами-решениями. Типичный пример трилеммы — ситуация с витязем на распутье: если прямо поедешь, то голову потеряешь; если направо поедешь — коня потеряешь; если налево поедешь — женату быть. Структурные требования дилеммы так же относимы и к трилемме и поэтому на ней останавливаться нет необходимости.
Когда же в условно-разделительном умозаключении выбор предстоит из более чем трех взаимоисключающих решений (вариантов), то такое умозаключение называется полилеммой. Некоторые же и трилемму называют полилеммой, поэтому у них всего два вида лемматических умозаключений: дилемма и полилемма.
Общая схема видов дедуктивных умозаключений интересна своей наглядностью, она позволяет едином взором охватить их все:
Виды дедуктивных умозаключений
(силлогизмов)
простой категорический
силлогизм
первая вторая третья четвертая
фигура фигура фигура фигура
4 4 6 5
модуса модуса модусов модусов
условный
силлогизм
разделительный
силлогизм
чисто условно-
условный категорический
разделительно- чисто
категорический разделительный
сокращенные,
сложные и
сложно-сокращенные
категорические
силлогизмы
энтимема эпихейрема
полисиллогизм сорит
условно-разделительный
(лемматический)
дилемма трилемма полилемма
конструктивная деструктивная
Глава 5
ИНДУКТИВНЫЕ И ТРАДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
ИНДУКЦИЯ, ЕЕ СТРУКТУРНЫЕ ОСОБЕННОСТИ, ВИДЫ
Индуктивное умозаключение — это мыслительная структура (форма мысли), вид умозаключения, в котором общий вывод следует из двух и более частных или… В виде схемы структура индуктивного умозаключения имеет такой вид: S1 есть РМЕТОДЫ НАУЧНОЙ ИНДУКЦИИ
Метод единственного сходства, или просто метод сходства, — это умозаключение о причине наблюдаемого явления, основанное на сравнении нескольких… 1-й случай: БВГ — обстоятельства, предшествующие явлению "в" 2-й случай: ДЕВ — обстоятельства, предшествующие явлению "в"ТРАДУКТИВНЫЕ УМОЗАКЛЮЧЕНИЯ
Традуктивные умозаключения — это рассуждения, в которых посылки и заключение являются суждениями одинаковой степени общности. Если дедукция —… Пять больше трех Три больше двухГлава 6
ФОРМЫ НАУЧНОГО МЫШЛЕНИЯ
К научным формам мысли правомерно отнести проблему (вопрос), доказательство (опровержение), гипотезу и теорию, поскольку эти формы мысли и стимулируют научные исследования, и способствуют обоснованию получаемых ими результатов, и свидетельствуют о довольно сложном характере данных форм мысли, и, кроме того, являются формами опережающего познания. Конечно, к научным формам мысли следует отнести и принцип, закон, категорию и некоторые другие, но поскольку они по структуре своей могут соответствовать в одних случаях понятиям, в других случаях - суждениям, то они как бы и не требуют особого рассмотрения с формально-логической позиции, ибо эти формы мысли уже исследованы. Но если к ним подходить с содержательной их стороны, то такой подход будет выходить за рамки предмета и задач формальной логики, и поэтому данные формы мысли, скорее, - предмет исследования теории познания (гносеологии), чем логики.
§ 1. ПРОБЛЕМА (ВОПРОС)
Проблема — форма мысли, отражающая и выражающая в виде вопроса (задачи, задания, системы их) наше знание о неизвестном (наше знание о незнании), и своей постановкой требующая теоретического или практического преодоления этой неизвестности, т.е. разрешения проблемы. Проблема, таким образом, и форма мысли, и форма организации исследования чего бы то ни было; она носит стимулирующий научное исследование, а в целом и любой человеческий труд, характер. Проблема — это вопрос, ответ на который не всегда содержится в накопленном знании и требует дополнительных теоретико-практических, т.е. физических или интеллектуальных, а то и тех и других одновременно, усилий, исследований. Она всегда связана с некоторой практической или теоретической трудностью, требующей физических, интеллектуальных усилий, преодоления неопределенности, результатом которой и выступает решение проблемы. Можно говорить о проблеме для себя, для отдельного человека (группы людей), и можно выделять проблемы для человечества, для общества в целом. Если решения первых проблем обычно уже содержится в накопленном знании и требуются лишь дополнительные, как правило, индивидуальные усилия для нахождения соответствующих связей между знаниями и проблемой (задачей, заданием и пр.), то вторые - более существенны, важны и ответ на них обычно не содержится в наличном знании (базисе), а требует дополнительного поиска таких знаний, дополнительного исследования и соответствующих усилий.
Проблема возникает обычно, когда встречается какое-то затруднение, когда что-то неясно, и эту неясность необходимо снять, устранить. Если неясность не имеет четкой формулировки, то эта неопределенность выступает как предпроблемная ситуация, как неопределенное затруднение. Со временем, конечно, эта неопределенность снимается, проблема формулируется четко и ясно.
Структурно вопрос и проблема состоят из одинаковых элементов. Вопрос, зачастую, — это форма выражения проблемы, а проблема — такой вопрос, ответ на который временно или принципиально затруднен. Вопрос — форма мысли, отражающая недостаточность исходной информации и структурными составляющими своими ориентирующая человека на ее преодоление. В языковой оболочке вопрос как форма мысли выражается вопросительным предложением. В структуре проблемы и вопроса обычно выделяют базис (основу), т.е. исходную информацию, затруднение и ориентацию.
Базис (основа), или предпосылка вопроса, — это то накопленное знание, та исходная информация, в которой и обнаруживается некое непреодолимое содержанием базиса затруднение, указывающее, что базис недостаточен, что его необходимо для преодоления затруднения расширить, углубить, дополнить. Неполнота и необходимость преодоления недостаточности исходной информации в вопросе выделяются такими операторами, как "кто", "что", "когда", "почему", "как" и пр. Эти же операторы выступают и ориентирующими элементами.
По разным основаниям выделяют довольно много видов, или типов вопросов: простые вопросы и сложные, полные и неполные, осмысленные и неосмысленные, содержательные и несодержательные, определенные и неопределенные, правильно поставленные (корректные) и неправильно поставленные (некорректные, каверзные), "к-вопросы" и "ли-вопросы" и т.п. Поскольку еще нет общепринятой классификации вопросов, скажем только о наиболее распространенных их типах.
Восполняющие, или "к-вопросы" — это вопросы с операторами, "как", "кто", "когда", "где", "что" и пр. Среди них различают простые вопросы — с одним из этих операторов, и сложные — состоящие из нескольких простых операторов, например: "Кто, где, когда и как ...?". Сложные "к-вопросы" всегда можно разбить на несколько простых. Содержанием своим "к-вопросы" направлены на поиски недостающего знания, и в ответ они требуют точной и исчерпывающей информации.
Уточняющие же вопросы, или "ли-вопросы", требуют ответов лаконичных, однозначных - "да" или "нет". Они, в свою очередь, делятся на простые безусловные с оператором "верно ли, что", и простые условные с операторами "верно ли, что если.., то", а также на сложные конъюнктивные, сложные дизъюнктивные, сложные импликативные вопросы. Понятно, что последние состоят из конъюнктивно, дизъюнктивно и импликативно связанных между собой простых "ли-вопросов", составляющих сложные.
Логически корректными, правильно поставленными будут те вопросы, базисы которых (предпосылки) — истинные суждения, например: "Как дойти до Киева?". Некорректными, неправильно поставленными, а то и каверзными будут те вопросы, базисы которых (предпосылки) ложны или неопределенны, например: "Кто отец Кащея Бессмертного?", "Как пройти туда, не знаю куда?", "Как найти то, не знаю что?", "Где в Африке находится город Курск?" и т.п. Полным считается тот вопрос, который содержит в себе и информацию о той области, где следует искать неизвестное, например: "В какой части Европы находится государство Люксембург?".
Для правильной постановки вопроса следует выполнять такие логические нормы:
1. Вопрос должен быть корректно поставлен. Каверзные, провокационные и неопределенные вопросы недопустимы.
2. Вопрос должен быть простым, т.е. кратким, ясным, четким. Длинные, запутанные вопросы затрудняют их понимание, усложняют ответ на них, а порой и лишают возможности дать правильный ответ. Сложные вопросы лучше разбивать на несколько простых.
3. В сложных разделительных вопросах необходимо перечислять все члены деления (альтернативы).
4. Наконец, последнее, поскольку вопрос не есть суждение, то не следует приписывать ему истинностные характеристики суждения.
Так как вопрос зачастую выступает формой выражения проблемы, то эти правила можно рассматривать и как правила проблемы.
Вопрос, как и проблема, раскрывает свою сущность лишь в единстве (в связи, сопоставлении) с ответом, с решением. Ответ должен быть четким, ясным, определенным, информативным, непротиворечивым, нетавтологичным; он должен снимать или, по крайней мере, уменьшать неопределенность вопроса. Ответы могут быть прямыми или косвенными, полными, исчерпывающими или частичными, допустимыми или недопустимыми, правильными или неправильными и пр. Допустимыми могут быть прямые, полные, частичные ответы. Недопустимыми — те, которые не согласуются с основой вопроса, с базисом, или нарушают правила.
Вопиющим примером недопустимого (по логике) вопроса, т.е. вопроса, формулировкой своей нарушающего логические нормы, является вопрос Всесоюзного референдума 17 марта 1991 г.: "Считаете ли вы необходимым сохранение Союза Советских Социалистических Республик как обновленной федерации равноправных суверенных республик, в которых в полной мере гарантированы права и свободы человека любой национальности?", с которым основная масса нашего народа связывала в то время возможность оказать влияние на наметившуюся тенденцию "разбегания" республик. Однако, результат референдума был предопределен.
С логической точки зрения вопрос сложен, и в силу этого ответ на него затруднен. Правильнее было бы, тем более для референдума, формулировать его в простом виде. В такой же формулировке он представляет собой совокупность нескольких, конъюнктивно связанных друг с другом вопросов. Конъюнкция, как известно, бывает правильной (дающей истинное сложное образование) только в одном случае, когда все входящие в него элементы обладают одной и той же значимостью. В данном же случае, как показал в результате своего логического анализа этого вопроса кандидат технических наук Юрий Грязнов в статье газеты "Смена" от 13 марта 1991 г. - на девять "да" всегда найдется одно "нет". Он разбил этот сложный вопрос на 9 простых и показал, что практически невозможно на все дать, как того требует референдум, одинаковый ответ. А раз так, то референдум теряет свое значение. "Например, - пишет Ю.Грязнов, - требование, чтобы все республики были советскими означает, что не допускается возможность, чтобы хоть одна из республик выбрала для себя иной способ народовластия, скажем, президентское правление или парламентскую республику. Далее, утверждение, что Союз должен быть сохранен, означает, по существу, что выход какой-либо республики из Союза исключается. Таким образом, этот вопрос фактически выносит на референдум статью Конституции о праве республик на выход из Союза. Наконец, необходимо заметить, что суверенные республики могут образовывать конфедерацию, но не федерацию, а образование федерации исключает суверенность республик, так что высказывания... являются несовместимыми, и давая ответ "да" на одно из них, вы обязаны дать ответ "нет" на второе...". С нарушителями своих законов природа беспощадна: нарушивший - да умрет! Нарушителям законов логики такая опасность не грозит, однако, чтобы достичь оптимально-эффективного результата в любом деле необходимо знать не только законы природы, общественные законы (правовые, экономические, законы производства, рынка) и пр., но и еще законы связи мыслей между собой.
§ 2. ДОКАЗАТЕЛЬСТВО (ОПРОВЕРЖЕНИЕ)
Доказательство — логическая форма мысли, обосновывающая истинность того или иного положения посредством других положений, истинность которых уже обоснована или самоочевидна. Поскольку свойством быть истинной или ложной обладает лишь одна из уже рассмотренных элементарных форм мысли, а именно - суждение, то речь в определении доказательства, естественно, идет о нем, и слово "положение" выступает в данном случае синонимом суждения. Иными словами, в доказательстве истинность того или иного суждения обосновывается обращением не к действительности, как это принято в обыденной повседневной практике, да порой и во многих науках, а к другим суждениям, истинность которых уже известна. Доказательство — это подлинно опосредованная мыслями форма отражения действительности, более оперативная и эффективная, поскольку манипуляция мыслями о предметах значительно проще манипуляции самими предметами; поскольку логические связи между мыслями обнаружить значительно легче, чем обнаруживать связи между самими предметами, наконец - логическими связями удобно пользоваться.
Доказательство в логике и в повседневной жизни понимается по-разному. В обыденности, в речи под доказательством понимают: факты, с помощью которых обосновывается истинность какого-то положения, т.е. саму действительность; источники сведений о фактах, документы, рассказы очевидцев, летописи, мемуары и пр. Логика же исследует доказательство только как мыслительную структуру, как форму мысли, как конструкцию логически связанных между собой нескольких мыслей, обосновывающих исходную мысль; как форму более сложную, чем умозаключение, поскольку доказательство может состоять из нескольких умозаключений. В отдельных случаях доказательство сводимо и к одному умозаключению. При этом структурно доказательство по своему строению как бы обратно умозаключению, т.е. между элементами доказательства и умозаключения имеется как сходство, так и различие.
Структурно доказательство, как и умозаключение, трехэлементно, в нем выделяют тезис, аргументы (или основания) и демонстрацию.
Тезис доказательства — это то положение, истинность которого следует обосновать. Понятно, что это положение может быть выражено только в форме суждения, ибо только оно может быть либо истинным, либо ложным. Тезиса в форме понятия быть не может, ведь понятия могут быть не только конкретными, единичными, общими, утвердительными и отрицательными, но и абстрактными, нулевыми, а вопрос об истинности последних просто некорректен.
Аргументы, или основания (иногда - посылки) — это те положения, которые используются для обоснования тезиса, истинность которых уже обоснована или не нуждается в обосновании в силу своей, как правило, умозрительной самоочевидности.
Демонстрация, или способ доказательства, — это вид логической связи как между самими аргументами, так и между аргументами и тезисом. Аргументы и тезис, поскольку они суть суждения, могут связываться между собой либо по фигурам категорического силлогизма, либо по правильным модусам условно-категорического, разделительно-категорического, условно-разделительного, чисто условного или чисто разделительного силлогизмов.
Сопоставляя структурные элементы доказательства и умозаключения, легко выделить определенное их сходство и различие. Простейшее доказательство может выглядеть в виде одного, как бы перевернутого умозаключения, например, простого категорического. Тезисом в этом доказательстве будет то суждение (положение), которое в силлогизме является выводом. Аргументами будут выступать посылки умозаключения, а демонстрацией — логическая связь между посылками, обуславливающая возможность вывода-тезиса. Если в силлогизме мы переходим от посылок к выводу, в доказательстве как бы наоборот — от тезиса к поиску аргументов, логическая связь между которыми и обосновывает тезис.
Анализируя каждый элемент структуры доказательства, логика сформулировала для них определенные правила, выступающие законами доказательства, соблюдение которых, в конечном счете, гарантирует не только структурную правильность доказательства, но и необходимую истинность обосновываемого тезиса, естественно, при истинности аргументов. Нарушения правил приводят к алогизмам. Сознательное нарушение правил — это софизм, нечаянное, непредумышленное нарушение — паралогизм. Правила эти таковы.
Правила тезиса:
1. Тезис должен быть четко и ясно сформулирован, без расплывчатости, двусмысленности, противоречивости.
2. Тезис на всем протяжении доказательства должен оставаться одним и тем же, самим собой.
Эти простые требования логики наиболее эффективно могут быть использованы лишь специалистами в своих предметных областях, потому что логик, не владея конкретным материалом в той или иной области, конечно же, не сможет заочно установить, достаточно ли четко сформулирован тот или иной тезис. Ошибочно думать, будто бы логика может научить специалистов других областей чуть ли не делать открытия. Вовсе нет. Требования логики при всей своей простоте, но в силу общности, нуждаются в конкретизации применительно к тому или иному предмету, к той или иной предметной области, а это всегда остается за специалистами в этих областях. Роль логики здесь методологическая, т.е. ориентирующая, направляющая, указующая, но не подменяющая специалиста, не решающая за него.
Наиболее типичными ошибками, связанными с нарушением правил тезиса, являются ошибки под названием "подмена тезиса", "слишком широкое доказательство", "слишком узкое доказательство", "довод к публике", "довод к человеку" и т. п.
Пример "довода к человеку". Студент приходит на экзамен (пусть это будет экзамен по логике) для доказательства, что он знает данный учебный предмет, т.е. его тезис формулируется примерно так: я знаю логику. Однако, часто вместо ответа на заданный контрольный вопрос по логике студент жалуется профессору, что у него проблемы с жильем, что его бытовые условия тяжелы, что стипендии не хватает, приходится подрабатывать, недосыпать, пропускать лекции, учебную литературу обстоятельно читать некогда и пр. Короче, профессору навязывается мысль, что предъявлять к такому студенту даже элементарную требовательность — жестоко, негуманно, что так может поступать только человек злой, каковым профессор, естественно, быть не захочет. Студент напирает на чувства, стремится вызвать сострадание к себе. О настоящем же тезисе экзаменационной ситуации, каковым должно быть знание логики, речь уже не идет. Тезис подменен. Приемов таких софистических уловок много, ими пользуются как сознательно, так и бессознательно. Все они не носят чисто логического характера. Приемы эти психологические. Человек по природе не может избавиться от особенностей своей психики, его восприятие эмоционально. Многие софистические уловки и опираются, они как бы расчитаны на эти особенности человека.
Трудно не попасться на такую уловку в следующем примере-задачке: "В автобусе едут 10 человек. На первой остановке входят 5 и выходят 2 человека. На второй остановке выходят 3 и не входит ни одного. На следующей — входят 7, а выходят 4 человека; на следующей — вошли 3 и не вышло ни одного, наконец, на последней остановке вышли 10 и вошли 4 человека. Сколько было... остановок?" Здесь только в конце задания становится ясно, что тезис изначально четко не выделен, умышленно не сформулирован, в задании сознательно акцентируются детали, имеющие косвенное отношение к тезису, т.е. тезис скрыто подменен, что является нарушением логики. Однако, именно в таком резком переходе и вся соль подобных задачек. Они - хороший психологический тренинг.
Правила аргументов (оснований):
1. Аргументы должны быть положениями истинными.
2. Истинность аргументов должна быть независимой от тезиса.
3. Аргументы должны являться достаточным основанием для тезиса, должны с необходимостью обосновывать тезис; тезис из аргументов должен следовать по законам логики, с необходимостью.
Очевидно, что и эти требования логики — просты и ясны до банальности. Тем не менее, не всегда так просто определить, какие же положения бесспорно истинны, какие же положения могут безусловно выступать в качестве аргументов, какие положения могут выполнять роль оснований для того или иного тезиса.
Вне всякого сомнения (такова уж их сущность, природа, такова их роль), в качестве аргументов могут выступать принципиальные положения (принципы, аксиомы, постулаты) любой науки (догматы церкви в рамках ее предметного поля), ибо эти положения являются исходными, основополагающими, заданными, устанавливающими "метрику" исследуемого предметного мира, или любой иной (даже идеальной, мнимой) предметной области. Они принимаются за истинные в силу своей предельной простоты, умозрительной самоочевидности или конвенции (или веры). Например: точка — это то, что не имеет частей. Понятно, что это положение не требуется обосновывать, доказывать, оно в своей простоте умозрительно самоочевидно. Это — аксиома. Или, -- мир един в своей материальности, материя первична, дух, сознание - вторичны. Эти положения одинаково невозможно логическими средствами ни обосновать, доказать, ни опровергнуть, их можно (что обычно и делается) принять или отвергнуть, проигнорировать, просто не знать, не обращать на них внимание и пр. С таким же успехом можно принять и иные, противоположные принципы, ибо и они логически недоказуемы, как и неопровержимы. Постулаты принимаются по договору, предположению, допущению.
Столь же несомненно и бесспорно, что в качестве аргументов могут выступать законы (законы природы, законы общества, законы мышления и познания). Обоснование этих законов обычно уже дано в той или иной науке, в той или иной области деятельности, и это обоснование обычно общезначимо, общепринято. Поэтому, любой сциентистски ориентированный человек в процессе доказательства своего тезиса может воспользоваться этими законами как аргументами, и они, в силу общепризнанности научного авторитета, будут выполнять роль веских и достаточных, необходимых аргументов. В качестве таковых могут выступать также и ранее обоснованные, доказанные положения, например, теоремы, определения и пр.
Сложнее обстоит дело, когда в качестве аргументов используются так называемые "факты". Если под ними понимают буквально самоочевидное в настоящее время, непосредственно воспринимаемое, то сами по себе такие факты не нуждаются в обосновании и могут использоваться как аргументы, но только в момент их непосредственного восприятия. Когда же речь идет о прошлом, о фактах бывшей действительности, которые приводятся то ли свидетелями, то ли документами, то ли описываются летописями, мемуарами и пр., тогда их "самоочевидность" сама становится проблемой. Разночтения в понимании этих фактов могут быть вызваны как тенденциозностью свидетелей, очевидцев; субъективностью восприятия ими этих фактов; односторонней целенаправленной их интерпретацией; так и из-за использовании различных средств, способов наблюдения, из-за различных точек зрения и пр. Как поступать в таких случаях, тем более, что факты, как известно, с одной стороны, — вещь сама по себе бессловесная (ведь, факты отражаются и интерпретируются людьми); с другой — упрямая и даже доказательная.
Верно, адекватно отраженный в суждениях факт, конечно же, может в отдельных случаях быть основанием для доказательства тезиса. Но поскольку адекватность отражения факта во многом зависит, определяется чисто человеческими, только что отмеченными свойствами, поскольку на отражение факта может оказывать влияние и неосознаваемое, подсознательное, то или иное состояние психики, а то и болезнь, настроение и пр., то один и тот же факт может быть отражен и понят людьми по-разному. Для снятия разногласий в понимании одного и того же факта, чтобы факты стали подлинными аргументами, в них следует выявлять общее, к ним следует подходить, учитывая их существенные, коренные, основные признаки и свойства, естественную их взаимосвязь между собой; факты следует рассматривать в системе, всесторонне, во взаимосвязи. Это осознавали многие, но наиболее известная, отражающая суть дела, цитата на этот счет из недалекого прошлого принадлежит В.И. Ленину, писавшему: "Факты, если взять их в их целом, в их связи, не только "упрямая", но и безусловно доказательная вещь. Фактики, если они берутся вне целого, вне связи, если они отрывочны и произвольны, являются именно только игрушкой или кое-чем еще похуже... Необходимо брать не отдельные факты, а всю совокупность относящихся к рассматриваемому вопросу фактов, без единого исключения, ибо иначе неизбежно возникает подозрение, и вполне законное подозрение, в том, что факты выбраны или подобраны произвольно, что вместо объективной связи и взаимозависимости исторических явлений в их целом преподносится "субъективная" стряпня для оправдания, может быть, грязного дела". (Ленин В.И. Полн. собр. соч. Т. 30. С. 350—351).
Ошибок, связанных с нарушением правил аргументов, много, назовем лишь некоторые, наиболее типичные и распространенные. Это — "ложный аргумент", "ложное основание", "основное заблуждение", "предвосхищение основания", "круг в доказательстве", "не следует, не вытекает", "от сказанного в относительном смысле, к сказанному в абсолютном смысле" и наоборот, и др.
Известный гоголевский герой, встречая православных, заметил, что все они едят галушки. На этом основании, особо не утруждая себя, он заключил, сформулировав свой тезис: всяк, кто не ест галушек, - басурманин. Вот другой пример "доказательства", приводимого Геродотом в его "Истории". Царь Египта Псамметих решил установить, какие люди древнейшие на свете. "Поэтому он придумал вот что. Царь велел отдать двоих новорожденных младенцев (от простых родителей) пастуху на воспитание среди стада (коз). По приказу царя никто не должен был произносить в их присутствии ни одного слова. Младенцев поместили в отдельной пустой хижине, куда в определенное время пастух приводил коз и, напоив детей молоком, делал все прочее, что необходимо. Так поступал Псамметих и отдавал такие приказания, желая услышать, какое первое слово сорвется с уст младенцев после невнятного детского лепета. Повеление царя было исполнено. Так пастух действовал по приказу царя в течение двух лет. Однажды, когда он открыл дверь и вошел в хижину, оба младенца пали к его ногам и, протягивая ручонки, произносили слово "бекос". Пастух сначала молча выслушал это слово. Когда затем при посещении младенцев для ухода за ними ему всякий раз приходилось слышать это слово, он сообщил об этом царю; а тот повелел привести младенцев перед свои царские очи. Когда же сам Псамметих услышал это слово, то велел расспросить, какой народ и что именно называет словом "бекос", и узнал, что так фригийцы называют хлеб. Отсюда египтяне заключили, что фригийцы еще древнее их самих". (Геродот. История. М., 1972. С. 80—81). Аргументом в этом "исследовании" служила сформированная в сознании Псамметиха еще до этого жестокого "эксперимента" установка, что первое слово любого ребенка, изолированного от влияния общества, будет и первым словом человечества. Это типичное "предвосхищение основания", "основное заблуждение".
Что касается правил демонстрации, то все они уже рассмотрены ранее. Так как связь аргументов между собой, связь аргументов и тезиса может осуществляться только по форме умозаключений, то правилами этой связи и выступают правила простого категорического силлогизма (как общие, так и правила фигур), условно-категорического, разделительно-категорического, чисто условного, чисто разделительного, условно-разделительного силлогизмов, силлогизмов отношения и пр. В некоторых случаях возможны в качестве правил демонстрации и правила методов научной индукции, поскольку вывод в них делается на основании хотя и опытного, наблюдаемого, но знания, отражающего главные, существенные, сущностные, определяющие связи и зависимости.
Общие правила категорического силлогизма, что из двух отрицательных (частных) посылок вывод с необходимостью не следует, или, что при отрицательности (частности) одной из посылок вывод будет только отрицательным (частным), что из положительных посылок отрицательный вывод не следует и пр. - все эти и другие правила простого категорического силлогизма вполне могут выступать правилами демонстрации доказательства, ибо нарушение любого из них приводит к алогизму, к логической ошибке. Ошибок, связанных с нарушением правил демонстрации, в силу их множественности, трудно перечислить, общее их название - "не следует", "не вытекает" и т.п.
Доказательство выполняет самую существенную роль в науке. Научное знание обязательно должно быть доказательным. Немаловажна роль доказательства в политике, дипломатии, в судебной практике, в педагогическом и воспитательном процессе, в пропаганде. Аристотель понимал доказательство как умение убеждать словом в ходе беседы, обсуждения, спора, полемики, дискуссии, в ходе обмена мыслями, и указывал, что люди только тогда более всего убеждаются в истинности того или иного положения, когда оно представляется им в виде доказательства, структура которого, обнажая связи между мыслями, и выступает убеждающим элементом. Действительно, именно тогда и происходит обоснование, аргументация того или иного положения {тезиса), когда становятся очевидными его связи с бесспорными, аргументативными положениями. В самом деле, все выступления, речи, лекции, научные работы ориентированы на обоснованность высказываемого, утверждаемого, отстаиваемого, на придание убедительности этому содержанию. И достичь такого результата стремятся не только содержательной насыщенностью, значимостью высказываемого, не только силой аргументов, но и их логической, закономерной взаимосвязью между собой.
Используемое в литературе слово "аргументация" явно производно от слова "аргумент" и должно бы пониматься, скорее, как процесс поиска необходимых и достаточных положений (оснований доказательства), процесс установления закономерных связей между ними, позволяющих тезису следовать из них с необходимостью. Тем не менее, это слово часто понимают как синоним доказательства, хотя аргументация и не тождественна логическому доказательству, она скорее соответствует тому, что можно назвать процессом доказательства, доказыванием. Доказательство структурно определенно, а аргументация в этом отношении довольно расплывчата. Распространенная многозначность повседневного словоупотребления способствует нечеткости в понимании аргументации, которую желательно снимать. Основной особенностью аргументации выступает то, что она более ориентирована на аргументы, на поиск веских, весомых, достаточных положений, в то время как доказательство немыслимо без логической взаимосвязи тезиса, аргументов и демонстрации, связи аргументов между собой, связи их с тезисом.
Аргументация иногда рассматривается как главное содержание всего логического учения, как его теория вывода, где вывод выступает завершающим аргументацию тезисом, но тогда аргументация даже более, чем доказательство. В нашей же интерпретации тезис доказательства выступает началом аргументации и он же завершает ее. Тезис формулируется до аргументов, затем следует их поиск (вот, собственно, что есть аргументирование, аргументация); найденные аргументы логически связываются как между собой, так и с тезисом (это тоже можно назвать аргументацией), и тезис, таким образом, завершает данный процесс. А это - структура доказательства.
Доказательство — логическая процедура обоснования тезиса, который вначале может выступать в виде проблемы (вопроса), задачи, требующей своего разрешения. В силу этого, процесс поиска разрешающих проблему (задачу), обосновывающих тезис аргументов становится наиболее важным в доказательстве. Поэтому, хотя тезис и является первым элементом доказательства, все-таки главным и определяющим элементом доказательства следует считать аргументы и логические связи между ними (аргументирование). Именно связи между аргументами, между аргументами и тезисом являются тем существенным элементом доказательства, который регламентируется формальной логикой.
Разумеется, в зависимости от характера тезиса способ аргументации будет особым. Ведь, в качестве аргументов могут выступать не только принципы, принципиальные положения наук, аксиомы, постулаты, законы (природы, общества, мышления и познания), ранее доказанные положения (теоремы, определения), самоочевидные факты реальности, совокупность их и пр., но и такие, например, положения, как "презумпция невиновности" в праве, или интуитивно разделяемые людьми принципы их взаимоотношений: "человек человеку — друг, брат и товарищ" или "человек человеку — волк" и т.п. Эти аргументы в их разнообразном сочетании могут быть использованы для обоснования как единичного, так и частного, общего тезиса.
В математике и математической логике наиболее распространен как вид доказательства метод аксиоматизации. Аргументация в этом случае выступает как процесс обоснования истинности того или иного тезиса посредством других истинных положений (аргументов) и в конечном счете как процесс должна опираться на принятые "начала", аксиомы. Если для диалектико-материалистической философии естественно обращение к реальности, поскольку для этой философии практика выступает не только источником, начальным моментом, основой всякого познания, но и его же критерием истины, то критерием правильности построения аксиоматических доказательств, или доказательств в рамках аксиоматических систем, выступает уже не действительность, а правила и требования, законы логики.
Логические требования относительно тех или иных рассуждений опираются, конечно же, и на структурные особенности форы мысли, и эти структуры могут выступать аргументами для некоторых выводов (тезисов). Структура той или иной мысли, как закономерная связь элементов, составляющих это целое, может выступать достаточным основанием для других мыслей, хотя и зависимых от первой, но являющихся иным, чем исходная, видом ее. Структура той или иной мысли может оказывать влияние на другие, более сложные мысли, на другие мысленные структуры, в которые она входит как составная часть. Так, истинная общая мысль "Все S есть Р" может сама по себе (самодостаточно) выступать аргументом для другой истинной мысли, что "Некоторые Р есть S", что "Все S не есть не-Р", что "Некоторые S есть Р", что "Все (или некоторые) не-Р не есть S". Эта же исходная мысль своей структурой определяет (аргументирует) ложность таких мыслей, как "Все (некоторые) S не есть Р". Структура суждения может оказывать влияние на умозаключение и т.п. И это аргументативно.
В том-то и проявляется методологическая роль логики, что она, не зная (отвлекаясь от) конкретного содержания наших мыслей, опираясь лишь на их структуру, используя известные логике закономерные связи элементов этих структур, позволяет делать определенные в истинностном отношении выводы. Поясним сказанное содержательным примером. Пусть исходной истинной мыслью будет общеутвердительное суждение "Все студенты - учащиеся". Согласно логике, эта мысль есть достаточное основание для получаемой из нее другой истинной мысли — "Некоторые студенты - учащиеся", "Некоторые учащиеся - студенты". И пусть такие мысли и не содержательно новые, но новые в логическом отношении, они — суждения другого вида. Если исходная мысль была общеутвердительной, то производные — частноутвердительные. Из этой же истинной исходной мысли можно получить и отрицательную истинную мысль: "Все студенты не есть не учащиеся" или "Все не учащиеся не есть студенты"; а также и частноотрицательную - "Некоторые студенты не есть не учащиеся" или "Некоторые не учащиеся не есть студенты". Истинность этой исходной мысли является также достаточным основанием для ложности такой мысли, как "Все (или некоторые) студенты не есть учащиеся". И такие, структурой определяемые зависимости по истине, присущи всем видам простых категорических суждений, да и не только им. Известны закономерные зависимости между элементами условного, разделительного и других суждений, которые тоже могут выступать достаточным основанием для определенных выводов из них. Таким образом, доказывание, аргументирование порой выступает умением применять требования и законы логики, ее теорию к тем или иным формам мысли, к мыслительным структурам, к процедурам рассуждений, и в аргументировании не всегда выделимы три элемента доказательства.
Аргументация может совершаться по-разному. Приведенные примеры — образцы непосредственной аргументации, но логика рассматривает и более опосредованные. Так, простой категорический силлогизм предполагает уже две посылки, два аргумента для обоснования истинности какого-то тезиса. Возможна и еще более сложная по своей структуре аргументация в виде полисиллогизма, как цепь умозаключений, где вывод предшествующего силлогизма становится аргументом для следующего.
Как правило, доказательство (аргументация) во всех областях знания проходит в виде сокращенных рассуждений, использующих энтимемы, эпихейремы, сориты и пр. Знание полной структуры этих мыслительных форм позволяет восстанавливать сокращенные умозаключения и, тем самым, проверять их логическую правильность.
Различают доказательства дедуктивного и индуктивного характера. Дедуктивные доказательства более распространены в математике, теоретической физике, философии и других науках, имеющих дело с неспецифицированными объектами, с объектами, не воспринимаемыми непосредственно. Индуктивные же доказательства — в опытных, экспериментальных, прикладного характера науках.
По способу доказывания, по типу связи аргументов и тезиса доказательства подразделяются на прямые и косвенные. Прямые доказательства — те, в которых тезис обосновывается аргументами непосредственно, прямо, т.е. используемые аргументы выполняют, например, роль посылок простого категорического силлогизма, где вывод из них выступает тезисом нашего доказательства. Иногда прямые доказательства называют еще и прогрессивными. Так, для доказательства тезиса "Мой друг сдает экзамен по логике" мы приводим следующие аргументы:
Мой друг - студент философского факультета и
Все студенты философского факультета сдают экзамен по логике.
Эти аргументы позволяют нам по модусу ВаrЬarа первой фигуры категорического силлогизма сразу получить вывод, совпадающий с нашим тезисом. Это — прямое, прогрессивное доказательство, состоящее из одного умозаключения, хотя доказательство и не обязательно сводимо к одному, доказательство может состоять и из нескольких умозаключений.
Это же самое доказательство может быть оформлено и в несколько ином, как бы свернутом, условно-категорическом виде: "Если все студенты философского факультета сдают экзамен по логике, то и мой друг сдает экзамен по логике, потому что он - студент философского факультета". Более точно условно-категорический силлогизм выглядит так:
Если все студенты философского факультета сдают экзамен по логике, то и мой друг сдает экзамен по логике
Мой друг - студент философского факультета
Мой друг сдает экзамен по логике.
Здесь, в первой посылке, в условном суждении сформулировано общее положение, во второй - в категорическом суждении - установлено, что основание условного суждения истинно. Согласно логической норме: при истинности основания условного суждения, следствие его будет обязательно истинно, - мы и получаем в качестве вывода наш тезис
Другое дело — косвенное доказательство, аналитическое, или регрессивное. В нем истинность тезиса обосновывается опосредованно, путем обоснования ложности антитезиса, т.е. положения (суждения), противоречащего тезису; либо путем исключения всех членов разделительного суждения по разделительно-категорическому силлогизму, кроме нашего тезиса, являющегося одним из членов этого разделительного суждения. В том и в другом случае необходимо опираться на требования логики к этим формам мысли, на законы и правила логики, строго соблюдать их. Так, при формулировке антитезиса надо следить за тем, чтобы он был действительно противоречащим тезису, а не противоположным ему, потому что противоречие не допускает одновременной ни истинности, ни ложности этих суждений (положений), а противоположность -допускает их одновременную ложность. При противоречии, обоснованная истинность антитезиса, выступает основанием ложности тезиса, а обоснованная ложность антитезиса, наоборот, косвенно обосновывает истинность тезиса. Обоснование же ложности противоположного тезису положения, не гарантирует, не обосновывает истинность самого тезиса, так как противоположные суждения могут быть и одновременно ложными. Косвенными доказательствами обычно пользуются тогда, когда нет аргументов для прямого доказательства, когда невозможно по разным причинам обосновать тезис прямо.
Общеизвестными образцами косвенного доказательства от противного, или путем приведения к абсурду, являются некоторые доказательства в геометрии. Например, не имея аргументов для прямого обоснования тезиса о том, что если две прямые параллельны третьей, то они параллельны и между собой, допускаем противное (постулат), а именно, что эти прямые не параллельны между собой. Раз так, значит они где-то пересекутся между собой и тем самым будут иметь общую точку. В этом случае получается, что через точку, лежащую вне третьей прямой, проходят две прямые, параллельные ей. А это противоречит ранее обоснованному положению, что через точку, лежащую вне прямой, можно провести только одну прямую, параллельную данной. Значит, наше допущение неверно, оно приводит к абсурду, к противоречию с уже известными истинами (или с принятыми аксиомами). В обобщенном, внесодержательном схематизированном виде это доказательство можно представить так: необходимо обосновать тезис В. Прямых аргументов для этого у нас нет. Допускаем, что истинно положение не-В. т.е. антитезис. Выводим из этого допущения следствия, например, не-С, не-Д. Когда в процессе сопоставления их с нашими основаниями (аксиомами), или с уже доказанными положениями, например, С, Д, обнаруживается несоответствие, противоречие между ними, то приходится с необходимостью признать ложность нашего допущения — ложность антитезиса. А этим, косвенно, доказывается (обосновывается) истинность тезиса.
Используются косвенные доказательства и в логике. Так, не имея прямых аргументов для обоснования тезиса: меньшая посылка в первой фигуре простого категорического силлогизма должна быть утвердительной, - допускаем противное, т.е. что она - отрицательная. Дальнейшее рассуждение показывает, что при отрицательности меньшей посылки, большая должна быть утвердительной, поскольку из двух отрицательных посылок вывод не следует. При отрицательности одной из посылок - вывод всегда отрицательный. В отрицательном выводе предикат должен быть распределен, поскольку во всех отрицательных суждениях предикат всегда распределен. Предикатом вывода в нашем случае есть понятие, являющееся предикатом большей утвердительной посылки. В утвердительных суждениях, известно, предикат как правило нераспределен. Вот тут-то и обнаруживается само противоречие - получается, что одно и то же понятие, не распределенное в посылке, как предикат утвердительного суждения, оказывается необходимо распределенным в заключении, как предикат отрицательного вывода. Логика своим требованием «термин, не распределенный в посылке, не может быть распределен в заключении» подобного не допускает. Таким образом, косвенно обосновывается тезис: меньшая посылка по первой фигуре должна быть суждением утвердительным.
Другой вид косвенного доказательства — разделительное доказательство. Оно обосновывает тезис путем исключения всех членов разделительного суждения, кроме тезиса. Ясно, что данный вид доказательства будет осуществляться по разделительно-категорическому или условно-разделительному силлогизмам. Например, возьмем тезис "S есть Р", или одним символом — В. Равносильными тезису являются положения "S есть P1", т.е. С; "S есть Р2", т.е. Д и т.д. В сокращенной записи это будет формула ВvСvД. При этом, В, С, Д должны полностью исчерпывать предметную область (наше деление должно быть соразмерным, полным), а члены деления должны исключать друг друга. Устанавливаем в каждом отдельном случае, что С ложно, что в действительности имеет место не-С. То же самое и относительно Д и т.д. И когда таким образом обоснуем ложность всех членов разделительного суждения, т.е. исключим члены деления, кроме нашего тезиса, только тогда можно с уверенностью считать, что тезис В косвенно обоснован. При этом, и это немаловажно, необходимо соблюсти все требования логики к разделительному суждению, к процессу деления объема данной предметной области. А главные требования логики к делению заключаются в том, чтобы расчленение предметной области совершалось по одному четкому признаку (основанию деления), чтобы деление при этом было последовательным (без скачков, пропусков), полным, соразмерным, чтобы члены деления исключали друг друга.
Из действий с доказательством, или над доказательством, как определенной формой мысли, определенной мыслительной структурой, наиболее известно всего лишь одно - отрицание его. Отрицание доказательства называется опровержением. Опровержение — это обоснование ложности или несостоятельности того или иного элемента доказательства, а иногда и доказательства в целом. Многие свойства опровержения определяются свойствами доказательства, потому что опровержение структурно мало чем отличается от доказательства. Опровержение может быть направлено против тезиса доказательства, против аргументов его, против демонстрации. Опровергая тезис, опровержение необходимо формулирует антитезис; опровергая аргументы - выдвигает другие; опровергая демонстрацию доказательства - показывает (демонстрирует) своей структурой строгое соблюдение логических связей между своими аргументами и антитезисом.
Обоснование истинности антитезиса можно рассматривать и как доказательство антитезиса, и как опровержение тезиса. Зато обоснование несостоятельности аргументов еще не доказывает ложности самого тезиса, а лишь указывает на ложность или недостаточность приведенных аргументов для обоснования тезиса, лишь отвергает их: вполне возможно, что таких аргументов много, но по разным причинам они в доказательстве не использовались. Таким образом, опровержение аргументов назвать антидоказательством не всегда возможно.
Так же и с опровержением демонстрации. Обосновывая неправильность (нелогичность, ошибочность) связи тезиса с аргументами, или связи между аргументами в доказательстве, мы лишь указываем на нарушение логики, но этим не отрицаем сам тезис, не отрицаем сами аргументы. И то, и другое может оказаться вполне приемлемым, стоит лишь найти более правильные непосредственные или опосредованные связи между ними. Поэтому, не всякое опровержение можно называть опровержением доказательства в целом, точнее, не всякое опровержение отбрасывает доказательство в целом. И это следует иметь в виду при определении опровержения.
Соответственно видам опровержения (опровержение тезиса, опровержение аргументов и опровержение демонстрации) можно указать и способы опровержения, которые используются в них. Так, тезис может быть опровергнут путем доказательства антитезиса и путем выведения следствий из тезиса, противоречащих действительности. Аргументы могут быть опровергнуты как путем обоснования их ложности (аргументы только кажутся истинными, или некритически принимаются за истинные), так и путем обоснования того, что для доказательства тезиса приведенных аргументов мало. Опровержение можно осуществить и путем обоснования того, что используемые аргументы сами нуждаются в обосновании. Ну и, наконец, опровержение можно осуществить и путем установления того, что источник фактов (оснований, аргументов) для обоснования тезиса является недостоверным, недоброкачественным: фальшивые документы, псевдолетописи, подделанные мемуары и пр.
Способов опровержения демонстрации, в силу множества самих правил демонстрации, достаточно много. Опровержением в этом случае будет указание на нарушение любого правила посылок категорического силлогизма при связи их между собой; указание на нарушение связи их с тезисом; указание на нарушение правил фигур категорического силлогизма и их модусов; указание на нарушение правил условного и разделительного силлогизмов и многое другое.
ГИПОТЕЗА И ТЕОРИЯ
Говоря о гипотезе, следует четко отличать ее от обычного, рядового предположения, потому что всякая гипотеза, конечно же, есть предположение, но не… Предположение и догадка могут в определенной степени носить субъективный… Рассмотрение гипотезы только как предположения сводит ее лишь к модальному суждению типа "возможно, что...".…ЗАКЛЮЧЕНИЕ
Хотя И. Кант и отмечал, что логика после Аристотеля, в силу своего совершенства, не сделала и шага вперед, что ее содержание уже не подвержено… Компьютеризация не только научно-технической, но даже и просто… Разработка парадоксов импликации привела к развитию разнообразных вариантов релевантных логик. В последние десятилетия…ЛОГИЧЕСКИЕ ОШИБКИ
Первым систематизатором логических (софистических и паралогистических) ошибок является Аристотель. Его работа "О софистических… Анализируя ошибки, Аристотель посчитал необходимым оговорить четыре рода… Аристотель выделяет шесть видов преднамеренных ошибок—софизмов, основывающихся на неправильном употреблении словесных…УПРАЖНЕНИЯ И ЗАДАЧИ
Понятие
дом, стол, человек, совесть, война, не-дом, безумство, белизна, севернее, национальность, не больше, деревянность; завод-гигант, летчик-космонавт,… Пример: "студент" — это простое, положительное, конкретное, общее,… 2. Изобразить в круговых схемах отношения между следующими понятиями:Суждение
Рыбы дышат жабрами. Часть народонаселения нашей планеты — белые. Не дано человеку прожить без греха. Только имеющие высшее образование могут… Пример: "Не все стихи запоминаются сразу" — Это предложение может… 2. Выразить в символическом виде структуру следующих суждений:Сложные суждения
Если воду нагреть, то она расширится. Линии бывают прямыми, или кривыми, или ломаными. Лекция была краткой, и интерес к ней не угасал на всем ее… Пример: "Если на улице идет дождь, то асфальт на улице мокрый" —… 2. Равносильны ли между собой (и почему) следующие пары формул сложных суждений:Умозаключение
1. Назвать составные элементы предложенных умозаключений:
Все французы суть европейцы
Некоторые виноделы — французы
Некоторые виноделы — европейцы.
Все рыбы дышат жабрами
Все киты не дышат жабрами
Все киты не есть рыбы.
Некоторые мои знакомые — студенты
Все студенты—учащиеся
Некоторые учащиеся — мои знакомые.
Все киты—млекопитающие
Все киты живут в воде
Некоторые живущие в воде—млекопитающие.
Пример: Все студенты — учащиеся
Иванов — студент
Иванов — учащийся.
В данном умозаключении роль субъекта выполняет слово "Иванов", т.е. это меньший термин умозаключения; соответственно и посылка, в которой он находится, является меньшей посылкой. Предикатом вывода является понятие "учащийся", это — больший термин; соответственно и посылка, в которой он находится, тоже большая. Средним термином этого умозаключения является понятие о студентах.
2. Составить из предложенных суждений умозаключения:
Все металлы — электропроводны.
Все планеты — шарообразны.
Все млекопитающие — позвоночные.
Все студенты — учащиеся.
Железо — электропроводно.
Золото есть металл.
Стекло не электропроводно.
Земля — планета.
Некоторые млекопитающие живут в воде.
Некоторые студенты — отличники.
Железо есть металл.
Земля шарообразна.
Золото — электропроводно.
Некоторые живущие в воде — позвоночные.
Все позвоночные — высокоорганизованные животные.
Все млекопитающие имеют красную кровь.
3. Нарушены ли законы логики (какие) в следующих умозаключениях:
Логика учит правильно рассуждать
Грамматика не есть логика
Грамматика не учит правильно рассуждать.
Все студенты — учащиеся
Некоторые студенты — спортсмены
Некоторые спортсмены — учащиеся.
Ни одна кошка не есть человек
Все люди смертны
Некоторые смертные не есть кошки.
Все студенты—учащиеся
Некоторые учащиеся — отличники
Некоторые отличники — студенты.
Все волки — хищники.
Это животное — хищник
Это животное — волк.
Некоторые учащиеся — отличники
Все студенты — учащиеся
Все студенты -- отличники
Все слова выражают какие-то мысли
Все жесты выражают какие-то мысли
Все жесты — слова.
Некоторые студенты — спортсмены
Все студенты — учащиеся
Некоторые учащиеся — спортсмены.
Фарфор не проводит электричества
Стекло не проводит электричества
Стекло есть фарфор.
Некоторые учащиеся — студенты
Некоторые студенты - отличники
Некоторые отличники — учащиеся.
Все рыбы живут в воде
Этот организм живет в воде
Этот организм — рыба.
Некоторые учащиеся — отличники
Некоторые учащиеся — студенты
Некоторые студенты — отличники.
Некоторые студенты — отличники
Некоторые учащиеся — студенты
Некоторыс учащиеся — отличники.
Пример: Все рыбы живут в воде
Инфузории живут в воде
Инфузории — рыбы.
Данное умозаключение построено по второй фигуре категорического силлогизма, так как средний термин в нем занимает место предиката в обеих посылках. В нем нарушено правило этой фигуры: одна из посылок должна быть суждением отрицательным. В данном же умозаключении обе посылки утвердительны. Вывод в таком случае не следует с необходимостью.
4. Что следует (и следует ли) из таких сочетаний:
В-->C B-->C B-->C B-->C B v C B v C B v C B v C
B Cне-B не-СB Cне-Вне-С
? ? ? ? ? ? ? ?
B-->C v D B-->C, D-->F B-->C, D-->F B-->C, D-->C M --- P
не-С v не-DB v D не-С v не-FB v D S --- M
? ? ? ? ?
5. Восстановить до полного силлогизма следующие энтимемы:
Наше дело правое, мы — победим. Все металлы электропроводны, а золото металл. Все газы при нагревании расширяются, поэтому и азот расширяется. Некоторые студенты отличники, а они бывают и медалистами.
Пример: "Юпитер, ты сердишься, значит -- ты не прав" — В данной энтимеме выводом является суждение "Ты (Юпитер) не прав", а меньшей посылкой, поскольку в ней находится субъект вывода "Юпитер", — суждение "Юпитер сердится". Зная, что средним термин отсутствует в выводе, но присутствует в посылках, легко определить, что им является понятие "сердиться". Теперь не сложно восстановить большую посылку, состоящую из предиката вывода и среднего термина:
Все сердящиеся не правы
Юпитер сердится_________ _
Юпитер не прав.
6. Проверить логическую правильность следующих эпихейрем:
Ложь вызывает недоверие, так как она извращает действительность
Лесть есть ложь, так как она есть умышленное извращение действительности
Лесть вызывает недоверие.
Все студенты сдают экзамены, так как они подтверждают этим свои знания Иванов — студент, так как он учится на нашем факультете
Иванов сдает экзамены.
Все спортсмены — физически развитые люди, так как они на тренировках выдерживают большие физические нагрузки
Некоторые студенты — спортсмены, так как они выступали на мировых чемпионатах
Некоторые студенты — физически развитые люди.
7. К какому виду полисиллогизмов относятся следующие:
Все позвоночные — теплокровные
Все млекопитающие — позвоночные
Все млекопитающие теплокровные
Все хищники — млекопитающие
Все хищники — теплокровные
Кошки - хищники
Кошки -- теплокровные.
Тигры -- позвоночные
Все позвоночные -- животные
Тигры -- животные
Животные есть организмы
Тигры -- организмы
Организмы материальны
Тигры -- материальны
Материальные образования изменяются
Тигры изменяются.
8. Проверить логическую правильность следующих соритов:
Все планеты вращаются вокруг Солнца
Земля — планета
Все вращающиеся вокруг Солнца планеты — шарообразны
Все шарообразные отбрасывают круглую тень
Земля отбрасывает круглую тень.
Все прямоугольники — параллелограммы
Все квадраты — прямоугольники
Все ромбы с прямыми углами — квадраты
Данная фигура есть ромб
Данная фигура—параллелограмм.
Буцефал есть лошадь
Лошадь -- четвероногое
Четвероногое есть животное
Животное есть живое
Живое есть организм
Организм есть материя
Буцефал есть материя.
Животное есть материя
Четвероногое есть материя
Лошадь есть четвероногое
Буцефал есть лошадь
Буцефал — материя
9. Выразить структуру условных силлогизмов в символическом виде:
Если на улице сильный дождь, то нам следует взять зонт; но если на улице сильный ветер, то нам следует надеть плащ
На улице или сильный ветер, или сильный дождь
Нам следует или взять зонт, или надеть плащ.
Если растение лишить кислорода, то оно погибнет
Растение не погибло
Растение не лишено кислорода.
Если Петров -- студент химического факультета, то он студент дневного факультета или студент вечернего
Петров или не студент дневного факультета, или не студент вечернего
Петров не студент химического факультета.
10. Выразить структуру разделительного силлогизма в символическом виде:
Треугольники являются остроугольными или неостроугольными
Неостроугольные треугольники - прямоугольные или тупоугольные
Треугольники являются остроугольными, или прямоугольными, или тупоугольными.
Студенты химического факультета или дневники, или вечерники
Данный студент химического факультета -- дневник
Данный студент химического факультета -- не вечерник.
Студенты — это учащиеся вузов или средних специальных учебных заведений
Данный студент — учащийся университета
Данный студент не учащийся среднеспециального учебного заведения.
Индукция
В Баку есть метро В Ереване есть метро В Тбилиси есть метроДоказательство
— Так как все студенты есть учащиеся, то и некоторые спортсмены нашего факультета тоже учащиеся. — Когда число делится на 20, то оно делится и на 5. Данное число делится на… — Всякий, кому суждено умереть, — умрет; всякий, кому суждено выздороветь, — выздоровеет. И умрет, и выздоровеет он…Опровержение
— Общее мнение, что здесь имела место месть, несостоятельно, ибо мститель руководствуется только личными мотивами, желанием воздать обидчику за… — Данное опровержение есть одновременно опровержение аргумента, ибо… — Заключение, что "Иванов — местный житель", сделанное на основании посылок "Все местные жители —…ЛИТЕРАТУРА
Основная
Аристотель. Органон // Соч.: В 4 т, Т. 2. М., 1976. Арно А., Николь П. Логика, или Искусство мыслить. М., 1991.Справочно-вспомогательная
Горский Д.П., Ивин А.А., Никифоров А.Л. Краткий словарь по логике. М., 1991. Жоль К.К. Логика в лицах и символах. М., 1993. Ивин А.А. Искусство правильно мыслить. М., 1990; По законам логики. М., 1992.– Конец работы –
Используемые теги: Логика0.034
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: ЛОГИКА
Что будем делать с полученным материалом:
Если этот материал оказался полезным для Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов