рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Философия
- /
- Базис векторов. Координаты вектора относительно базиса
Реферат Курсовая Конспект
Базис векторов. Координаты вектора относительно базиса
Базис векторов. Координаты вектора относительно базиса - раздел Философия, Элементы линейной алгебры и аналитической геометрии 1. Введенные Линейные Операции Позволяют Из Чисел И Векторов Составлять Выраж...
1. Введенные линейные операции позволяют из чисел и векторов составлять выражения вида
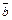 = a1
= a1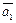 + a2
+ a2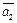 + … + an
+ … + an ,
,
которые называются линейной комбинацией векторов 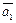 ,
, 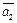 , …,
, …,  с коэффициентами a1, a2, …, an.
с коэффициентами a1, a2, …, an.
2. Система векторов 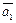 ,
, 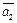 , …,
, …,  называется линейно независимой, если равенство
называется линейно независимой, если равенство
a1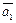 + a2
+ a2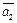 + … + an
+ … + an =
=  ,
,
возможно тогда и только тогда, когда все коэффициенты равны нулю. В противном случае она называется линейно зависимой.
3. Базисом векторного пространства называется упорядоченная система векторов { } такая, что:
} такая, что:
1) эта система линейно независима,
2) любой вектор пространства является линейной комбинацией векторов этой системы.
4. Число векторов в базисе называется размерностью пространства.
5. Базис называется ортонормированным, если базисные векторы являются ортами и ортогональны (перпендикулярны) друг другу. Для трехмерного пространства обозначение: 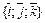 .
.
6. Если 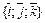 – базис трехмерного пространства, то для любого вектора
– базис трехмерного пространства, то для любого вектора 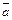 этого пространства существует единственная тройка чисел
этого пространства существует единственная тройка чисел
х1, х2, х3, таких, что
 . (5)
. (5)
Говорят, что вектор 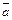 разложен по векторам базиса, а числа х1, х2, х3 называются коэффициентами разложения.
разложен по векторам базиса, а числа х1, х2, х3 называются коэффициентами разложения.
7. Декартовыми координатами вектора 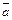 в базисе
в базисе 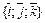 называются коэффициенты разложения этого вектора по базису. Обозначение:
называются коэффициенты разложения этого вектора по базису. Обозначение: 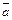 ={х1; х2; х3}. Один и тот же вектор в двух различных базисах имеет разные декартовы координаты.
={х1; х2; х3}. Один и тот же вектор в двух различных базисах имеет разные декартовы координаты.
8. Рассмотрим векторное пространство R3 и пусть  ,
, 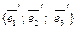 – два различных базиса. По формуле (5) имеют место разложения
– два различных базиса. По формуле (5) имеют место разложения 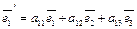 ,
,  и
и  . Эти равенства можно представить в виде матричного равенства:
. Эти равенства можно представить в виде матричного равенства:  . Матрица
. Матрица  называется матрицей перехода от базиса
называется матрицей перехода от базиса  к базису
к базису 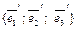 .
.
9. Пусть произвольный вектор  в базисе
в базисе  по формуле (5) имеет разложение
по формуле (5) имеет разложение 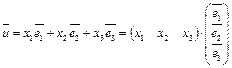 и пусть в базисе
и пусть в базисе 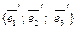 имеет разложение
имеет разложение 
 . Связь между старыми координатами
. Связь между старыми координатами  и новыми координатами
и новыми координатами 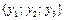 выражается формулой:
выражается формулой:
 ,
,
где А – матрица перехода от первого базиса ко второму.
– Конец работы –
Эта тема принадлежит разделу:
Элементы линейной алгебры и аналитической геометрии
Волжский институт строительства и технологий... филиал государственного образовательного учреждения... высшего профессионального образования...
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Базис векторов. Координаты вектора относительно базиса
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?







Новости и инфо для студентов