рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Кривые второго порядка

Реферат Курсовая Конспект

Выберите учебное заведение

Кривые второго порядка

Кривые второго порядка - раздел Философия, Элементы линейной алгебры и аналитической геометрии 1. Окружностью Радиуса R С Центром В ...

1. Окружностью радиуса R с центром в точке C(a; b) называется геометрическое место точек плоскости, для которых расстояние до центра С равно R. Каноническое уравнение окружности с центром в точке

и радиусом

(рис. 1):

Рис. 1

2. Параболой называется геометрическое место точек плоскости, одинаково удаленных от данной точки F, называемой фокусом и от прямой, называемой директрисой. Если фокус взять в точке

, а директрису задать уравнением

, где p > 0, то получим параболу (рис. 2), каноническое уравнение которой имеет вид:

Рис. 2

Если фокусы и директрисы брать тремя другими способами, то получим еще три параболы (табл. 1).

Таблица 1

Уравнение параболы	Фокус	Директриса

3. Эллипсом называется геометрическое место точек плоскости, сумма расстояний от которых до двух данных точек F₁ и F₂, называемых фокусами (|F₁F₂| = 2c) есть величина постоянная, равная 2a > 2c.

Каноническое уравнение эллипса (рис. 3):

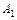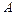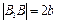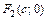Точки , , и – вершины эллипса; отрезок – большая ось, отрезок – малая ось; параметры и – большая и малая полуоси; точки и – левый и правый фокусы; число 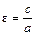– эксцентриситет; и – левый и правый фокальные радиусы. Параметры , и 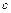связаны равенством .

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Элементы линейной алгебры и аналитической геометрии

Волжский институт строительства и технологий... филиал государственного образовательного учреждения... высшего профессионального образования...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Кривые второго порядка

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Баврин, И.И. Общий курс высшей математики / И.И. Баврин, В.Л. Матросов. – М.: Просвещение, 1995. – 464 с. 2. Данко, П.Е. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Поп

Матрицы
1. Числовой матрицей или просто матрицей называется прямоугольная таблица из чисел aij, состоящая из m строк и n столбцов и записывается в виде

Определители квадратных матриц
1. Определителем матрицы 2-го порядка называется число, равное

Системы линейных уравнений
1. В общем случае система m линейных уравнений с n неизвестными имеет вид (

Метод Гаусса
Метод Гаусса решения систем линейных уравнений состоит в том, что последовательным исключением неизвестных при помощи элементарных преобразований систему приводят к такому виду, чтобы матрица систе

Простейшие задачи на плоскости
1. Расстояние между двумя точками и

Различные виды уравнения прямой на плоскости
1. Углом наклона прямой к оси Ох называется наименьший положительный угол a (0 £ a < p), на который надо повернуть против часовой стрелки ось Ох до совмещения с данной прямой

Взаимное расположение двух прямых на плоскости
1. Угол между двумя прямыми и

Базис векторов. Координаты вектора относительно базиса
1. Введенные линейные операции позволяют из чисел и векторов составлять выражения вида =

Действия над векторами в координатной форме
1. Если и

Различные виды уравнения плоскости
1. Общее уравнение плоскости: , где

Взаимное расположение двух плоскостей
1. Угол между плоскостью с нормальным вектором

Различные виды уравнений прямой в пространстве
1. Общие уравнения прямой: где

Взаимное расположение двух прямых в пространстве
1. Угол между прямой с направляющим вектором

Взаимное расположение прямой с плоскостью
1. Угол между прямой с направляющим вектором