рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Основные правила дифференцирования

Реферат Курсовая Конспект

Выберите учебное заведение

Основные правила дифференцирования

Основные правила дифференцирования - раздел Философия, Введение в анализ. Дифференциальное исчисление. Функций одной переменной 20. ...

20. . 21. .

22. , C = const. 23. .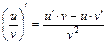

24. Дифференцирование сложной функции: пусть сложная функция y = f(j(x)) задана на интервале (a; b) и х₀ Î (a; b), тогда если внутренняя функция t = j(x) в точке х₀ имеет конечную производную , а внешняя функция y = f(t) в точке t₀ = j(x₀) имеет конечную производную , то сложная функция y = f(j(x)) в точке х₀ имеет конечную производную, которая вычисляется по правилу:

25. Дифференцирование функции, заданной параметрически: если функция задана параметрически то производная вычисляется по формуле: .

26. Дифференцирование функции, заданной неявно: если функция задана неявно уравнением , то для нахождения ее производной дифференцируют обе части этого уравнения, считая сложной функцией от и полученное уравнение разрешают относительно .

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Введение в анализ. Дифференциальное исчисление. Функций одной переменной

Волжский институт строительства и технологий... филиал государственного образовательного учреждения... высшего профессионального образования...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Основные правила дифференцирования

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

САМОСТОЯТЕЛЬНОЙ РАБОТЫ
1. Баврин, И. И. Общий курс высшей математики / И. И. Баврин, В. Л. Матросов. – М. : Просвещение, 1995. – 464 с. 2. Данко, П. Е. Высшая математика в упражнениях и задачах / П. Е. Данко, А.

Основные теоремы о действиях над функциями, имеющими конечный предел
7. . 8.

Виды неопределенностей
15. Если и

Замечательные пределы
18. Первый замечательный предел: . Он используется для раскрытия неопределенности вида

Непрерывность функции в точке. Точки разрыва
22. Пусть функция y = f(x) определена в некоторой окрестности точки x = a и в самой точке x = a. Функция непрерывна в точке, если: 1

Производные и дифференциалы высших порядков
27. Пусть функция y = f(x) на интервале (a; b) имеет непрерывную производную

Применения производной
32. Если на некотором промежутке , то на этом промежутке функция