Применения производной

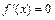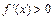32. Если на некотором промежутке , то на этом промежутке функция постоянна; если , то функция возрастает; если , то функция убывает.

33. Если функция непрерывна в точке и при переходе через точку первая производная меняет знак с «+» на «–», то в точке функция имеет максимум; если первая производная меняет знак с «–» на «+», то в точке функция имеет минимум.

34. График дифференцируемой на интервале (a; b) функции y = f(x) называется выпуклым, если на этом интервале он расположен ниже любой своей касательной (рис. 3, а) и называется вогнутым, если он расположен выше любой своей касательной (рис. 3, б).

Если на некотором промежутке 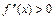, то на этом промежутке функция вогнута; если , то функция выпукла.

35. Если функция непрерывна в точке и при переходе через точку вторая производная меняет знак, то точка – точка перегиба.

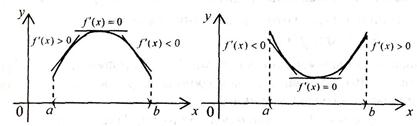
а) б)