Тема 10. Статистическое изучение взаимосвязи социально-экономических явлений

Задача 1.Имеются данные о величине средней урожайности зерновых ц/га и затратах на минеральные удобрения руб/ га пашни по хозяйствам района (табл. 27).

 

Таблица 27

№	Исходные данные	Расчетные данные
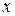
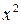
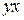
	9,49
	7,57
	9,95
	9,23
	11,97
	8,56
	11,18
	7,93
	15,75
	13,61
	2,99
	12,57
	10,93
	9,86
	7,39
	9,23
	15,4
	13,14
	12,12
	10,27
	9,12
	13,42
	10,29
	14,55
	15,26
Итого	271,78				х
В среднем	10,87	66,64	х		х
	2,9261	13,1602	х	х	х

 

Необходимо:

1. Рассчитать коэффициент парной линейной корреляции, парной линейной детерминации, сделать выводы по каждому коэффициенту.

2. Построить уравнение парной линейной регрессии, спрогнозировать 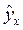при различных значениях фактора, то есть рассчитать:

· максимально возможную величину ;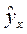

· минимальную ;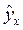

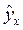· для средних значений фактора.

3. Провести статистическую оценку:

· уравнения регрессии;

· параметров уравнения регрессии и коэффициент корреляции.

Решение.

1. Рассчитаем коэффициент парной линейной корреляции:

Коэффициент парной линейной корреляции показывает, что затраты на минеральное уравнение оказывают сильное влияние на величину урожайности зерновых.

Коэффициент парной линейной детерминации рассчитывается как квадрат коэффициента парной линейной корреляции;

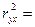
Показывает, что _____% всей вариации результативного признака обусловлено включенным в модель фактором.

2. Уравнение парной линейной регрессии имеет вид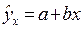

При расчете параметров уравнения при помощи МНК необходимо решить систему из двух нормальных уравнений.

Рассчитаем все возможные значения в таблице 27 подставим в систему;

Разделим первое уравнение на ____, а второе на ______.

Вычтем из второго уравнение первое

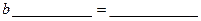
Отсюда

Подставим в первое уравнение систему и рассчитаем :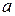

Получили уравнение парной линейной регрессии:

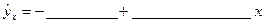
Параметр , называется коэффициентом регрессии. В задаче он показывает, что при увеличении затрат на минеральные удобрения на 1 руб/га пашни средняя урожайность зерновых, в среднем, возрастет на ____________ ц/га.

Подставляя в уравнение значение фактора 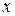рассчитаем – табл. 27.

Рассчитаем максимально возможную величину 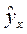. Коэффициент регрессии 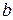положителен, поэтому возьмем максимальное значение фактора 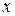(при отрицательном значении 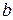берем минимальное значение фактора ).

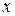Рассчитаем минимально возможную величину 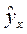. Коэффициент регрессии 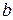положителен, поэтому возьмем минимальное значение фактора 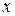(при отрицательном значении 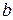берем максимальное значение фактора ).

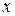Рассчитаем величину 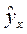при средних значениях фактора .

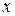3. Проведем статистическую оценку уравнения регрессии его параметров и коэффициента корреляции.

Статистическую значимость уравнения регрессии определяют при помощи критерия Фишера ().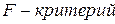

Рассчитаем фактическое значения критерия Фишера:

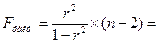
Теоретическое значение берем таблицы 5%-го уровня распределения F (приложение 1).

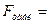
Так как 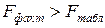, уравнение регрессии признается статистически значимым.

Статистическую значимость параметра 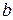и коэффициента корреляции 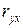определяют при помощи критерия Стьюдента ().

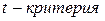Для парной линейной модели фактическое значения .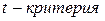

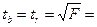
Табличное значение 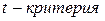берем из таблицы «Значение критерия t Стьюдента при уровне значимости 0,10, 0,05 и 0,01» (приложение 2)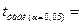

Так как, фактические значения критерия Стьюдента больше табличных коэффициент регрессии и корреляции следует признать статистически значимым.

 

Приложение 1

Таблица 5%-го уровня распределения F (уровень значимости 0,05)

v₁ – число степеней свободы для большей дисперсии;

v₂ – число степеней свободы для меньшей дисперсии.

v2	v2
	18,51	19,00	19,16	19,25	19,30	19,33	19,36	19,37
	10,13	9,55	9,28	9,19	9,01	8,94	8,88	8,84
	7,71	6,94	6,59	6,39	6,26	6,16	6,09	6,04
	6,61	5,79	5,41	5,19	5,05	4,95	4,88	4,82
	5,99	5,14	4,76	4,53	4,39	4,28	4,21	4,15
	5,59	4,74	4,35	4,12	3,97	3,87	3,79	3,73
	5,32	4,46	4,07	3,84	3,69	3,58	3,50	3,44
	5,12	4,26	3,86	3,63	3,48	3,37	3,29	3,23
	4,96	4,10	3,71	3,48	3,33	3,22	3,14	3,07
	4,84	3,98	3,59	3,36	3,20	3,09	3,01	2,95
	4,75	3,88	3,49	3,26	3,11	3,00	2,92	2,85
	4,67	3,80	3,41	3,18	3,02	2,92	2,84	2,77
	4,60	3,74	3,34	3,11	2,96	2,85	2,77	2,70
	4,54	3,68	3,29	3,06	2,90	2,79	2,70	2,64
	4,49	3,63	3,24	3,01	2,85	2,74	2,66	2,59
	4,45	3,59	3,20	2,96	2,81	2,70	2,62	2,55
	4,41	3,55	3,16	2,93	2,77	2,66	2,58	2,51
	4,38	3,52	3,13	2,90	2,74	2,63	2,55	2,48
	4,35	3,49	3,10	2,87	2,71	2,60	2,52	2,45
	4,32	3,47	3,07	2,84	2,68	2,57	2,49	2,42
	4,30	3,44	3,05	2,82	2,66	2,55	2,47	2,40
	4,28	3,42	3,03	2,80	2,64	2,53	2,45	2,38
	4,26	2,40	3,01	2,78	2,62	2,51	2,43	2,36
	4,24	3,88	2,99	2,76	2,60	2,49	2,41	2,34
	4,22	3,37	2,98	2,74	2,59	2,47	2,39	2,32
	4,21	3,35	2,96	2,73	2,57	2,46	2,37	2,30
	4,20	3,34	2,95	2,71	2,56	2,44	2,36	2,29
	4,18	3,33	2,93	2,70	2,54	2,43	2,35	2,28
	4,17	3,32	2,92	2,69	2,53	2,42	2,34	2,27
	4,08	3,23	2,84	2,61	2,45	2,34	2,25	2,18
	4,03	3,18	2,79	2,56	2,40	2,29	2,20	2,13
	4,00	3,15	2,76	2,52	2,37	2,25	2,17	2,10
	3,94	3,09	2,70	2,46	2,30	2,19	2,10	2,03
∞	3,84	2,99	2,60	2,37	2,21	2,09	2,01	1,94

Окончание прил. 1

Таблица 5%-ного уровня распределения F (уровень значимости 0,05)

v₁ – число степеней свободы для большей дисперсии

v₂ – число степеней свободы для меньшей дисперсии

v2	v1
								∞
	19,38	19,39	19,40	19,41	19,42	19,43	19,44	19,46	19,50
	8,81	8,78	8,76	8,74	8,71	8,69	8,66	8,62	8,53
	6,00	5,96	5,93	5,91	5,87	5,84	5,80	5,74	5,63
	4,78	4,74	4,70	4,68	4,64	4,60	4,56	4,50	4,36
	4,10	4,06	4,03	4,00	3,96	3,92	3,87	3,81	3,67
	3,68	3,63	3,60	3,57	3,52	3,49	3,44	3,38	3,23
	3,39	3,34	3,31	3,28	3,23	3,20	3,15	3,08	2,93
	3,18	3,13	3,10	3,07	3,02	2,98	2,93	2,86	2,71
	3,02	2,97	2,94	2,91	2,86	2,82	2,77	2,70	2,54
	2,90	2,86	2,82	2,79	2,74	2,70	2,65	2,57	2,40
	2,80	2,76	2,72	2,69	2,64	2,60	2,54	2,46	2,30
	2,72	2,67	2,63	2,60	2,55	2,51	2,46	2,38	2,21
	2,65	2,60	2,56	2,53	2,48	2,44	2,39	2,31	2,13
	2,59	2,55	2,51	2,48	2,43	2,39	2,33	2,25	2,07
	2,54	2,49	2,45	2,42	2,37	2,33	2,28	2,20	2,01
	2,50	2,45	2,41	2,38	2,33	2,29	2,23	2,15	1,96
	2,46	2,41	2,37	2,34	2,29	2,25	2,19	2,11	1,92
	2,43	2,38	2,34	2,31	2,26	2,21	2,15	2,07	1,88
	2,40	2,35	2,31	2,28	2,23	2,18	2,12	2,04	1,84
	2,37	2,32	2,28	2,25	2,20	2,15	2,09	2,00	1,81
	2,35	2,30	2,26	2,23	2,18	2,13	2,07	1,98	1,78
	2,32	2,28	2,24	2,20	2,14	2,10	2,04	1,96	1,76
	2,30	2,26	2,22	2,18	2,13	2,09	2,02	1,94	1,73
	2,26	2,24	2,20	2,16	2,11	2,06	2,00	1,92	1,71
	2,27	2,22	2,18	2,15	2,10	2,05	1,99	1,90	1,69
	2,25	2,20	2,16	2,13	2,08	2,03	1,97	1,88	1,67
	2,24	2,19	2,15	2,12	2,06	2,02	1,96	1,87	1,65
	2,22	2,18	2,14	2,10	2,05	2,00	1,94	1,85	1,64
	2,21	2,16	2,12	2,09	2,04	1,99	1,93	1,84	1,62
	2,12	2,07	2,04	2,00	1,95	1,90	1,84	1,74	1,51
	2,07	0,02	1,98	1,95	1,90	1,85	1,78	1,69	1,44
	2,04	1,99	1,95	1,92	1,86	1,81	1,75	1,65	1,39
	1,97	1,92	1,88	1,85	1,79	1,75	1,68	1,57	1,28
∞	1,83	1,83	1,79	1,75	1,69	1,64	1,57	1,46	1,00

 

Приложение 2

Значение критерия t Стьюдента при уровне значимости 0,10, 0,05 и 0,01

n	a	n	a
0,10	0,05	0,01	0,10	0,05	0,01
	6,3138	12,706	63,657		1,7341	2,1009	2,8784
	2,9200	4,3027	9,9248		1,7291	2.0930	2,8609
	2,3534	3,1825	5,8409		1,7247	2,0860	2,8453
	2,1318	2,7764	4,6041		1,7207	2,0796	2,8314
	2,0150	2,5706	4,0321		1,7171	2,0739	2,8188
	1,9432	2,4469	3,7074		1,7139	2,0687	2,8073
	1,8946	2,3646	3,4995		1,7109	2,0639	2,7969
	1,8595	2.3060	3,3554		1,7081	2,0595	2,7874
	1,8331	2,2622	3,2498		1,7056	2,0555	2,7787
	1,8125	2,2281	3,1693		1,7033	2,0518	2,7707
	1,7959	2,2010	3,1058		1,7011	2,0484	2,7633
	1,7823	2,1788	3,0545		1,6991	2,0452	2,7564
	1,7709	2,1604	3,0123		1,6973	2,0423	2,7500
	1,7613	2,1448	2,9768		1,6839	2,0211	2,7045
	1,7530	2,1315	2.9467		1,6707	2,0003	2,6603
	1.7459	2,1199	2,9208		1.6577	1,9799	2,6174
	1,7396	2,1098	2,8982		1,6449	1,9600	2,5758