LINEAR PROGRAMMING

GRAPHICAL LINEAR PROGHAkCKHG SOLUTION

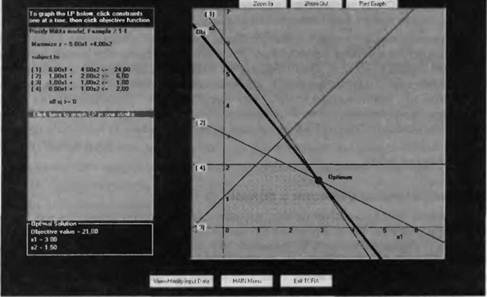
Рис. 2.4. Графическое решение модели Reddy Mikks, полученное в системе TORA

При необходимости можно удалить график, а затем нарисовать его заново. Для этого щелкните на записи all xj>= 0 (все переменные неотрицательные) в левой час­ти окна. Чтобы просмотреть или изменить условия задачи, щелкните на кнопке View/Modify Input Data (Просмотр/Изменение входных данных). Затем можно снова решить задачу с новыми исходными значениями.

2.2. Графическое решение задачи линейного программирования

УПРАЖНЕНИЯ 2.2.3

1. Режим обучения в программе TORA. В программе TORA введите следую­щие условия задачи ЛП и укажите, что решение следует получить в гра­фическом режиме.

Максимизировать г = Sx₁ + 8х₂ при выполнении условий

х, + х₂>8,

2х_г-3х₂<0,

х, + 2х₂ < 30,

Зх, -х₂>0,

х,<10,

х₂>9,

х„ х₂>0.

Далее на листе бумаги начертите оси х, и х₂ в подходящем для этой задачи мас­штабе (в программе TORA можно щелкнуть на кнопке Print Graph (Распечатать график), которая расположена в верхней правой части окна, чтобы получить раз­графленный лист). Теперь самостоятельно начертите первое ограничение. Для проверки можно щелкнуть на соответствующем ограничении в левой части ок­на программы. Начертите все остальные ограничения. Затем постройте целе­вую функцию. Проверьте, правильно ли вы усвоили графическое решение за­дачи ЛП, повторив все выполненные действия в системе TORA.

2. Рассмотрим модель Reddy Mikks (файл ch2ToraReddyMikks.txt). С помощью TORA покажите, что оптимальное решение задачи ЛП всегда связано с угловой точкой пространства решений. Сначала введите (или загрузите) исходную модель ЛП. Найдите ее графическое решение. Затем, щелкнув на кнопке View/Modify Input Data (Просмотр/Изменение исходных данных), вернитесь в окно ввода дан­ных и введите представленные ниже уравнения целевых функций. В результа­те вы должны увидеть, что при изменении угла наклона целевой функции оп­тимальные решения будут находиться в различных угловых точках. Цель этого упражнения — показать, что для того, чтобы найти оптимальное реше­ние задачи ЛП, достаточно знать угловые точки пространства решений.

a) г = 5х, + х₂.

b) г = 5х_х + 4х₂.

c) 2 = + Зх₂.

d) z = - х, + 2х₂.

e) г = - 2х, + х₂.

f) 2 = - х, - х_г.

3. В модели "диеты" (файл ch2ToraDiet.txt) замените целевую функцию сле­дующей:

минимизировать z = 0,8х, + 0,8х₂.

Используя графические возможности системы TORA, покажите, что опти­мальное решение связано с двумя различными угловыми точками, причем в обеих точках оптимальное решение будет одинаковым. В этом случае гово­рят, что задача имеет альтернативный оптимум. Объясните, какие условия

Глава 2. Введение в линейное программирование

привели к такой ситуации, и покажите, что на самом деле задача имеет бес­конечное множество альтернативных оптимумов. Затем напишите формулу для определения всех таких решений.

4. Рассмотрим следующую модель ЛП:

максимизировать z = 5х, + 4х₂ при выполнении условий

6х, + 4х₂<24, б^ + Зх^гг.б, х, + х₂ < 5, х, + 2х₂<6, - х, + х₂< 1, х₂<2, х„ х₂>0.

В ЛП ограничение называется избыточным, если его удаление из модели не изменяет пространство допустимых событий. Используя систему TORA, оп­ределите, какие ограничения избыточны. Затем покажите, что их удаление не повлияет на пространство решений и оптимум.

5. Используя систему TORA, покажите, что если в модели Reddy Mikks удалить ог­раничения на ресурсы (первые два ограничения), то пространство решений будет неограниченным. Что в этом случае можно сказать об оптимальном решении?

Предположим, что в модель Reddy Mikks добавлено еще одно ограничение: х₂ > 3.

6. Используя систему TORA, покажите, что полученная модель содержит про­тиворечивые ограничения, которые одновременно не могут быть удовлетво­рены. Поэтому модель не имеет допустимых решений.

2.3. ГРАФИЧЕСКИЙ АНАЛИЗ ЧУВСТВИТЕЛЬНОСТИ

Модель линейного программирования является как бы "моментальным сним­ком" реальной ситуации, при которой параметры модели (коэффициенты целевой функции и неравенств ограничений) предполагаются неизменными. Естественно изучить влияние изменения параметров модели на полученное оптимальное реше­ние задачи ЛП. Такое исследование называется анализом чувствительности.

В этом разделе анализ чувствительности основывается на графическом решении задачи ЛП. Рассмотрим два случая: 1) изменение коэффициентов целевой функции и 2) изменение значений констант в правой части неравенств ограничений. Хотя проведенное здесь исследование будет элементарным и ограниченным, оно пока­жет основные идеи методов анализа чувствительности. Подробно методы этого анализа описаны в главе 4.

2.3.1. Изменение коэффициентов целевой функции

В общем виде целевую функцию задачи ЛП с двумя переменными можно запи­сать следующим образом.

Максимизировать или минимизировать z = с₁х₁ + с₂х₂.

Изменение значений коэффициентов с, и с₂ приводит к изменению угла наклона прямой 2. Графический способ решения задачи ЛП, описанный в разделе 2.2, показы-

2.3. Графический анализ чувствительности

вает, что это может привести к изменению оптимального решения: оно будет достигать­ся в другой угловой точке пространства решений. Вместе с тем, очевидно, существуют интервалы изменения коэффициентов c_t и с₂, при которых текущее оптимальное реше­ние сохраняется. Задача анализа чувствительности и состоит в получении такой ин­формации. В частности, представляет интерес определение интервала оптимальности для отношения cjc₂ (или, что то же самое, для с₂/с,); если значение отношения с,/с₂ не выходит за пределы этого интервала, то оптимальное решение в данной модели со­храняется неизменным. Следующий пример показывает, как можно получить необ­ходимый результат с помощью анализа графического представления модели ЛП.

Пример 2.3.1

Применим процедуру анализа чувствительности к задаче примера 2.2.1 (модель для компании Reddy Mikks). На рис. 2.5 видно, что функция z = Ьх_х +4дг₂ достигает максимального значения в угловой точке С. При изменении коэффициентов целе­вой функции z = c_ix₁ + cj₂ точка С останется точкой оптимального решения до тех пор, пока угол наклона прямой z будет лежать между углами наклона двух пря­мых, пересечением которых является точка С. Этими прямыми являются 6jtj + 4jc₂ = 24 (ограничение на сырье Ml) и л, + 2х₂ = 6 (ограничение на сырье М2). Алгебраически это можно записать следующим образом:

В первой системе неравенств условие с, ф О означает, что прямая, соответствующая целевой функции, не может быть горизонтальной. Аналогичное условие в следую­щей системе неравенств означает, что эта же прямая не может быть вертикальной. Из рис. 2.5 видно, что интервал оптимальности данной задачи (он определяется двумя прямыми, пересекающимися в точке С) не разрешает целевой функции быть ни горизонтальной, ни вертикальной прямой. Таким образом, мы получили две системы неравенств, определяющих интервал оптимальности в нашем примере. (Если с_х и с₂ могут принимать нулевые значения, интервал оптимальности для от­ношения cjc₂ (или с₂/с,) необходимо разбить на два множества, где знаменатели не обращались бы в нуль. Эта ситуация представлена в упражнении 2.3.1.1.)

Итак, если коэффициенты с_х и с₂ удовлетворяют приведенным выше неравенст­вам, оптимальное решение будет достигаться в точке С. Отметим, если прямая z = c_lx_i + CjX₂ совпадет с прямой х_х + 2х₂ = 6, то оптимальным решением будет любая точка отрезка CD. Аналогично, если прямая, соответствующая целевой функции, совпадет с прямой 6л, + 4х₂ = 24, то любая точка отрезка ВС будет оптимальным решением. Однако заметим, что в обоих случаях точка С остается точкой опти­мального решения.

Приведенные выше неравенства можно использовать при определении интервала оптимальности для какого-либо одного коэффициента целевой функции, если предположить, что другой коэффициент остается неизменным. Например, если

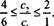
с, фО,

или

с, фо.

Глава 2. Введение в линейное программирование

в нашей модели зафиксировано значение коэффициента с₂ (пусть с₂ = 4), то интер-

1 с 6

вал оптимальности для коэффициента с. получаем из неравенств — < —<— путем

2 с, 4

подстановки туда значения с₂ = 4. После выполнения элементарных арифметиче­ских операций получаем неравенства для коэффициента c_t: 2<с₁<6. Аналогично, если зафиксировать значение коэффициента с, (например, c_t = 5), то из неравенств

Рис. 2.5. Интервал оптимальности для модели Reddy Mikks

УПРАЖНЕНИЯ 2.3.1

1. Определите графически интервал оптимальности для отношения с,/с₂ в сле­дующих задачах; отдельно рассмотрите случаи, когда коэффициенты с₅ и с₂ могут обращаться в нуль.

a) Максимизировать z = 2х_х + Зх₂ при выполнении условий

Зх₁ + 2х_г<6, -х₁ + х₂<0, x_ltx₂>0.

b) Максимизировать z = бх, + Зх₂ при выполнении условий

Зх, + 2х_г < 6,

2.3. Графический анализ чувствительности

х, - х_г < О, х„ х₂>0.

с) Максимизировать z = х, + х₂ при выполнении условий

-х, + х₂<0, Зх, -х₂<3, х„ х₂>0.

2. В задаче "диеты" из примера 2.2.2:

a) определите интервал оптимальности для отношения стоимости фунта ку­курузной муки к стоимости фунта соевой муки;

b) если стоимость фунта кукурузной муки увеличится на 20%, а стоимость фунта соевой уменьшится на 5%, то будет ли в этом случае оптимальным ранее найденное решение?

c) если стоимость фунта кукурузной муки останется фиксированной (30 центов), а стоимость фунта соевой муки возрастет до 1,10 долл., то ос­танется ли оптимальным ранее найденное решение?

3. Магазин В&К продает два вида безалкогольных напитков: колу А1 известно­го производителя и колу В&К собственного производства. Доход от одной банки колы А1 составляет 5 центов, тогда как доход от одной банки собст­венной колы — 7 центов. В среднем магазин за день продает не более 500 ба­нок обоих напитков. Несмотря на то что А1 — известная торговая марка, по­купатели предпочитают колу В&К, поскольку она значительно дешевле. Подсчитано, что объемы продаж колы В&К и А1 (в натуральном исчислении) должны соотноситься не менее 2:1. Кроме того, известно, что магазин прода­ет не менее 100 банок колы А1 в день.

a) Сколько банок каждого напитка должен иметь магазин в начале рабочего дня для максимизации дохода?

b) Определите соотношение доходов от напитков А1 и В&К, при котором со­храняется оптимальное решение, найденное на предыдущем этапе.

4. Мебельная фабрика для сборки столов и стульев привлекает к работе на 10 дней четырех столяров. Каждый столяр тратит 2 часа на сборку стола и 30 ми­нут — на сборку стула. Покупатели обычно приобретают вместе со столом от четырех до шести стульев. Доход от одного стола составляет 135 долл. и 50 долл. — от одного стула. На фабрике установлен 8-часовой рабочий день.

a) Определите графически структуру производства (на 10 рабочих дней), ко­торая максимизировала бы суммарный доход.

b) Определите для найденного решения интервал оптимальности для отно­шения доходов на единицу продукции.

c) Изменится ли найденное выше оптимальное решение, если доходность из­готовления столов и стульев уменьшится на 10% ?

d) Изменится ли найденное выше оптимальное решение, если доходность из­готовления столов и стульев составит соответственно 120 и 25 долл. на единицу продукции?

5. Банк Elkins в течение нескольких месяцев планирует вложить до 200 000 долл. в кредитование частных лиц (клиентов) и покупок автомоби­лей. Банковские комиссионные составляют 14% при кредитовании частных

Глава 2. Введение в линейное программирование

лиц и 12% при кредитовании покупок автомобилей. Оба типа кредитов воз­вращаются в конце годичного периода кредитования. Известно, что около 3% клиентских и 2% автомобильных кредитов никогда не возвращаются. В этом банке объемы кредитов на покупку автомобилей обычно более чем в два раза превышают объемы других кредитов для частных лиц.

a) Найдите оптимальное размещение средств по двум описанным видам кре­дитования и определите коэффициент возврата по всем кредитам.

b) Определите интервал оптимальности для отношения процентных ставок по двум видам кредитов для найденного на предыдущем шаге оптималь­ного решения.

c) Предположим, что невозврат кредитов составит 4 и 3 % для кредитов ча­стных лиц и кредитов на покупку автомобилей соответственно. Изменит­ся ли при этом оптимальное решение, полученное выше?

6. Завод Electra производит два типа электрических двигателей, каждый на от­дельной сборочной линии. Производительность этих линий составляет 600 и 750 двигателей в день. Двигатель первого типа использует 10 единиц некоего комплектующего, а двигатель второго типа — 8 единиц этого же компонента. Поставщик может обеспечить на день 8000 единиц этих деталей. Доходность изготовления двигателя первого типа составляет 60, второго — 40 долл.

a) Определите оптимальную структуру ежедневного производства двигателей.

b) Найдите интервал оптимальности для отношения доходности двигателей.

7. Консервный завод Рореуе перерабатывает за смену 60 000 фунтов спелых по­мидоров (7 пенсов за фунт) в томатный сок и пасту. Готовая продукция паке­тируется в упаковки по 24 банки. Производство одной банки сока требует од­ного фунта спелых помидоров, а одной банки пасты — трети фунта. Заводской склад может принять за смену только 2 000 упаковок сока и 6 000 упа­ковок пасты. Оптовая цена одной упаковки томатного сока составляет 18 долл., одной упаковки томатной пасты — 9 долл.

a) Определите оптимальную структуру производства консервного завода.

b) Найдите отношение оптовых цен на продукцию завода, при котором заво­ду будет выгоднее производить больше томатной пасты, чем сока.

8. Мебельная фабрика собирает из готовых комплектующих два вида кухонных шкафов: обычные и дорогие. Обычный шкаф покрывается белой краской, а до­рогой — лаком. Покраска и покрытие лаком производятся на одном производ­ственном покрасочном участке. Сборочная линия фабрики ежедневно может собирать не более 200 обычных шкафов и 150 дорогих. Лакирование одного до­рогого шкафа требует вдвое больше времени, чем покраска одного простого. Если покрасочный участок занят только лакированием дорогих шкафов, то за день здесь можно подготовить 180 таких шкафов. Фабрика оценивает доход от обычных и дорогих кухонных шкафов в 100 и 140 долл. соответственно.

a) Сформулируйте задачу линейного программирования и составьте опти­мальное ежедневное расписание работы покрасочного участка.

b) Предположим, что в результате конкуренции доход от производства одно­го обычного шкафа снизился до 80 долл., а дорогого — до 110 долл. Ис­пользуя анализ чувствительности, определите, будет ли в этой ситуации решение, полученное на предыдущем этапе, оптимальным.

2.3. Графический анализ чувствительности

2.3.2. Доступность ресурсов

Во многих моделях линейного программирования ограничения трактуются как условия ограниченности ресурсов. В таких ограничениях правая часть неравенств является верхней границей количества доступных ресурсов. В этом разделе мы изучим чувствительность оптимального решения к изменению ограничений, нала­гаемых на ресурсы.

Пример 2.3.2

В модели для компании Reddy Mikks (пример 2.2.1) первые два неравенства пред­ставляют собой ограничения на использование сырья Ml и М2 соответственно. Напомним, что в данной задаче оптимальное решение достигается в угловой точ­ке С, являющейся точкой пересечения прямых, соответствующих ограничениям на сырье Ml и М2 (рис. 2.6). При изменении уровня доступности материала Ml (увеличение или уменьшение текущего уровня, равного 24 т) точка С оптималь­ного решения "плывет" вдоль отрезка DG. Любое изменение уровня доступности материала Ml, приводящее к выходу точки пересечения С из этого отрезка, ведет к неосуществимости оптимального решения в точке С. Поэтому можно сказать, что конечные точки 0=(2,2)иС= (6, 0) отрезка DG определяют интервал осу­ществимости для ресурса Ml. Количество сырья Ml, соответствующего точке D = (2, 2), равно 6х, + 4х₂ = 6x2+4x2 = 20 т. Аналогично количество сырья, со­ответствующего точке G = (6, 0), равно 6x6 + 4x0 = 36т. Таким образом, ин­тервал осуществимости для ресурса Ml составляет 20 < M_t < 36 (здесь через Ml

Рис. 2.6. Интервал осуществимости для ресурса Ml

Глава 2. Введение в линейное программирование

обозначено количество материала Ml). Если мы определим М, как Л/, = 24 + D_v где Dj — отклонение количества материала Ml от текущего уровня в 24 т, то по­следние неравенства можно переписать как 20 < 24 + D_; < 36 или -4 < D, < 12. Это означает, что текущий уровень ресурса Ml может быть уменьшен не более чем на 4 т и увеличен не более чем на 12 т. В этом случае гарантируется, что оптималь­ное решение будет достигаться в точке С— точке пересечения прямых, соответ­ствующих ограничениям на ресурсы Ml и М2.

Теперь рассмотрим ресурс М2. На рис. 2.7 видно, что интервал осуществимости для ресурса М2 определяется конечными точками В и Н отрезка ВН, где В = (4, 0) и Н = (8/3, 2). Точка Н находится на пересечении прямых ED и ВС. Определяем, что коли­чество сырья М2, соответствующего точке В, равно л:, + 2х₂ = 4 + 2x0=4 т, а точке Н— 8/3 + 2x2= 20/3т. Значение целевой функции в точке В равно 5х₁ + 4х₂ = 5x4 + 4x0 = 20 (тыс. долл.), а в точке Н — 5 х 8/3 + 4x2 = 64/3 (тыс. долл.). Отсюда следует, что количество сырья М2 может изменяться от 4 до 20/3 тонн.

"2 Интервал осуществимости для материала М2

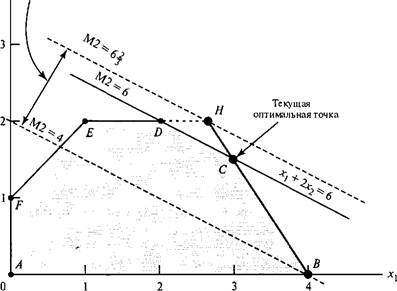
Рис. 2.7. Интервал осуществимости для ресурса М2

2.3.3. Стоимость ресурсов

На рис. 2.8 показано, что модель ЛП можно представить как модель "вход-выход", где ограниченные ресурсы соответствуют входу модели, а значение целе­вой функции — выходу. Чувствительность модели можно оценить по степени влияния входа (ресурсов) на выход (значение целевой функции). Простую меру чувствительности можно получить как побочный продукт вычисления интервалов осуществимости для ресурсов, выполненного в разделе 2.3.2. В частности, опреде­лим стоимость единицы ресурса, как отношение изменения значения целевой функции к изменению доступного количества ресурсов.

2.3. Графический анализ чувствительности

Обозначим через y_t стоимость ресурса i. Эта стоимость вычисляется по формуле _ изменение значения z, соответствующего интервалу осуществимости ресурса i интервал осуществимости ресурсаi

Проиллюстрируем этот показатель на примере модели Reddy Mikks.

г-

Ресурсы модели

 

 

 

 

 

	Модель Л П	W
W
W	W
W

Значение целевой функции модели

Рис. 2.8. Представление модели ЛП как модели "вход-выход"

Пример 2.3.3

На рис. 2.6 видно, что при изменении количества сырья Ml от 20 до 36 тонн (интервал осуществимости ресурса Ml) значения целевой функции z будут соответ­ствовать положению точки Сна отрезке DG. Обозначив через у_х стоимость единицы ресурса Ml, получим следующую формулу.

изменение значения z при перемещении т. С от D до G

У1 =

изменение количества Л/, при перемещении т. С от D до G

Если точка С совпадает с точкой D = (2, 2), то z = 5 х 2 + 4 х 2 = 18 (тыс. долл.), если же точка С совпадает с точкой G = (6, 0), тогда г = 5х6 + 4х0 = 30 (тыс. долл.). От­сюда следует, что

30 — 18 з

у, =——— = — (тыс. долл. на тонну материала Ml).

Этот результат показывает, что изменение количества ресурса Ml на одну тонну (если общее количество этого ресурса не меньше 20 и не больше 36 тонн) приводит к изменению в оптимальном решении значения целевой функции на 750 долл. Теперь рассмотрим ресурс М2. Для него интервал осуществимости составляет от 4 до 20/3 тонн. На рис. 2.7 видно, что этот интервал определяется конечными точ­ками В и Я отрезка ВН. Таким образом,

изменение значения z при перемещении т. С от В до //

У г '

изменение количества Л/, при перемещении т. С от В до //

Значение целевой функции в точке В равно Ъх_х + 4х, = 5x4 + 4x0 = 20 (тыс. долл.), а в точке Н — 5 х 8/3 + 4 х 2 = 64/3 (тыс. долл.). Отсюда следует, что

64/3-20 1 . _ил1 у₂ = ^ —— = — (тыс. долл. на тонну материала М2).

Этот результат показывает, что изменение количества ресурса М2 на одну тонну (если общее количество этого ресурса не меньше 4 и не больше 20/3 тонн) приводит к изменению в оптимальном решении значения целевой функции на 500 долл.

Глава 2. Введение в линейное программирование

УПРАЖНЕНИЯ 2.3.2

1. Фабрика Wild West производит два типа ковбойских шляп. Производство шляпы первого типа требует в два раза больше временных ресурсов, чем из­готовление шляпы второго типа. Если фабрика будет производить только шляпы второго типа, то в день она сможет изготовить 400 таких шляп. Рынок налагает ограничения на производство шляп: не более 150 шляп пер­вого и 200 шляп второго типа. Доход от производства шляп составляет 8 долл. на единицу первого типа и 5 долл. — второго типа.

a) Примените графический метод для определения ежедневного оптималь­ного производства шляп обоих типов.

b) Определите стоимость увеличения производства на одну шляпу второго типа и интервал значений числа ежедневного производства этих шляп, для которого данная стоимость была бы применима.

c) Используя стоимость единицы ресурса, определите, на сколько изменится максимальный доход фабрики, если ежедневное производство шляп пер­вого типа не будет превышать 120 единиц.

d) Чему равна стоимость увеличения предельного спроса на одну шляпу вто­рого типа?

2. Компания производит два вида продукции, А и В. Объем продаж продукта А составляет не менее 80% от общего объема продаж продуктов А и В. Вместе с тем, компания не может производить более 100 единиц продукта А в день. Для производства этих продуктов используется одно и то же сырье, поступ­ление которого ограничено 240 фунтами в день. На изготовление единицы продукта А расходуется 2 фунта сырья, а единицы продукта В — 4 фунта. Цена одной единицы продуктов А и В составляет 20 и 50 долл. соответственно.

a) Найдите оптимальную структуру производства этой компании.

b) Определите стоимость единицы сырья и интервал изменения потребляе­мого сырья, при котором справедлива данная стоимость.

c) С помощью графического анализа чувствительности определите, как из­менится значение целевой функции при изменении максимального уров­ня производства продукта А на ±10 единиц.

3. Компания на производство двух продуктов в день тратит 10 часов. Производ­ство каждого продукта состоит из последовательного выполнения трех процес­сов. Данные по этим продуктам и процессам приведены в следующей таблице.

	Процесс 1 Процесс 2 Процесс 3	Доход
Продукт	(количество минут выполнения процесса на единицу продукта)	(на единицу продукта), долл.
	10 6 8
	5 20 10

a) Определите структуру оптимального производства.

b) Предположим, что появилась возможность увеличить время на выполне­ние одного из трех процессов. Для выбора процесса, время которого будет увеличено, создайте логически обоснованные приоритеты процессов.

2.3. Графический анализ чувствительности

4. Компания Show&Sell имеет возможность рекламировать свою продукцию по местному радио и телевидению. Бюджет на рекламу ограничен суммой 10 ООО долл. в месяц. Одна минута рекламного времени на радио стоит 15, а на телевидении — 300 долл. Компания предполагает, что реклама на радио по времени должна превышать рекламу на телевидении не менее чем в два раза. Вместе с тем, известно, что нерационально использовать более 400 минут рекламы на радио в месяц. Последние исследования показали, что реклама на телевидении в 25 раз эффективнее рекламы на радио.

a) Разработайте оптимальный бюджет для рекламы на радио и телевидении.

b) Определите стоимость единицы месячного лимита на рекламу по радио.

c) Вычислив стоимость единицы ресурса, определите возможную эффектив­ность рекламной кампании при увеличении ежемесячного бюджета на рекламу до 15 000 долл.

5. Корпорация Wyoming Electric является собственником электрогенерирую-щей станции. Поскольку эта корпорация имеет богатые запасы угля, на электростанции для генерации электрического тока используется уголь. Агентство по защите окружающей среды установило следующие ограниче­ния: концентрация выбрасываемого в воздух сернистого газа не должна пре­вышать 0,002, количество выбрасываемых аэрозольных частиц не должно превышать 20 фунтов в час. Корпорация для генерации электрического то­ка использует пылевидный уголь двух сортов, С1 и С2. Перед сжиганием эти сорта угля обычно смешиваются. Для простоты предположим, что сер­нистая составляющая в смеси углей определяется как средневзвешенное от доли угля каждого сорта в смеси. Характеристики используемых сортов угля приведены в следующей таблице.

Сорт угля	Концентрация Количество выделяемых серы (%) аэрозольных частиц (фунт/час)	Количество вырабатываемого пара (фунт/час)
С1	0,18 2,1	12 000
С2	0,21 0,9	9 000

a) Найдите оптимальную смесь углей обоих сортов.

b) На сколько изменится количество вырабатываемого пара (в час), если ос­лабить на 1 фунт в час ограничение на количество выбрасываемых аэро­зольных частиц?

6. Факультет послевузовского обучения местного колледжа города Озарк пред­лагает в общей сложности до 30 курсов каждый семестр. Все курсы условно можно разбить на два типа: практические, такие как деревообработка, обу­чение работе на компьютере, ремонт и поддержка автомобилей и т.п.; и гу­манитарные, например история, музыка и изобразительное искусство. Что­бы удовлетворить запросы обучающихся, в каждом семестре должно предлагаться не менее 10 курсов каждого типа. Факультет оценивает доход от одного практического курса в 1500, а гуманитарного — в 1000 долл.

a) Какова оптимальная структура курсов для факультета?

b) Определите, какой доход будет иметь факультет при увеличении на 1 ми­нимального количества практических курсов.

c) Определите доход факультета при увеличении минимального количества гуманитарных курсов на 1.

Глава 2. Введение в линейное программирование

7. Швейная фабрика Burroughs производит мужские сорочки и женские блузки для магазина Walmark. Этот магазин согласен принимать всю продукцию фабрики Burroughs. Производство швейного изделия состоит из раскроя, пошива и пакетирования готового изделия. На участке раскроя работают 25 человек, непосредственно на пошиве изделий — 35 человек и пакетируют готовые изделия 5 человек. Швейная фабрика Burroughs работает в одну смену (8 часов) пять дней в неделю. Трудозатраты на выпускаемые фабрикой изделия и доход от них показаны в следующей таблице.

Изделие	Раскрой	Пошив	Пакетирование	Доход
		(минуты на изделие)		(в долл. на изделие)
Рубашка				8,00
Блузка				12,00

a) Определите оптимальную структуру еженедельного производства для этой швейной фабрики.

b) Вычислите стоимость одного часа рабочего времени, затрачиваемого от­дельно на раскрой, пошив и пакетирование.

c) Предположим, что можно организовать сверхурочную работу на участках раскроя и пошива. Какую максимальную почасовую добавку за сверх­урочные может предложить швейная фабрика?

8. Завод бытовой химии производит два вида чистящих средств, А и В, исполь­зуя при этом сырье I и II. Для производства чистящих средств ежедневно имеется 150 единиц сырья. На получение одной единицы средства А исполь­зуется 0,5 единицы сырья I и 0,6 единицы сырья И. На производство одной единицы средства В затрачивается 0,5 единицы сырья I и 0,4 единицы сырья II. Доход на одну единицу средств А и В составляет соответственно 8 и 10 долл. Ежедневное производство средства А должно быть не менее 30 и не более 150 единиц. Для производства средства В аналогичные ограничения состав­ляют 40 и 200 единиц.

a) Найдите оптимальную структуру выпуска чистящих средств.

b) Определите стоимость единицы изменения граничных значений ежеднев­ного выпуска средств А и В.

9. Конвейер состоит из трех последовательных линий для сборки двух видов радиоприемников: HiFi-1 и HiFi-2. Время, необходимое для сборки одного радиоприемника на каждой линии, приведено в следующей таблице.

 

Сборочная линия	Количество минут, затрачиваемых на сборку одного изделия
HiFi-1	HiFi-2

Ежедневные профилактические работы на соответствующих линиях состав­ляют 10, 14 и 12% от всего рабочего времени, которое для любой линии не превышает 480 минут в смену.

2.4. Компьютерное решение задач ЛП

a) Определите структуру выпускаемой продукции, при которой минимизи­руется время простоя всех трех линий.

b) Вычислите стоимость одного процента уменьшения времени профилакти­ческих работ для каждой линии.

2.4. КОМПЬЮТЕРНОЕ РЕШЕНИЕ ЗАДАЧ ЛП

Графический метод, описанный в разделе 2.2, основывается на некоторых фун­даментальных свойствах оптимального решения задач ЛП. Но на практике, когда типичная задача линейного программирования содержит сотни и даже тысячи пе­ременных и ограничений, графический метод неприменим. Здесь требуется ис­пользование компьютерных программ.

В этом разделе мы рассмотрим решение задач ЛП с помощью программы TORA, средства Excel Поиск решения, а также программ AMPL и LINGO. Программа TORA и средство Поиск решения предназначены для решения задач средних размеров. Для решения больших задач, содержащих сотни (и даже тысячи) ограничений и перемен­ных, необходимо использовать коммерческие программы, такие как AMPL и LINGO.

2.4.1. Решение задач ЛП с помощью TORA

Ввод необходимых для решения задачи данных в программе TORA прост и по­нятен и не нуждается в дополнительных инструкциях. Поэтому в этом разделе мы основное внимание уделим интерпретации результатов, получаемых с помощью этой программы.

Пример 2.4.1

На рис. 2.9 показана выходная распечатка решения задачи ЛП для компании Reddy Mikks (пример 2.2.1), выполненная программой TORA. На примере этой неодно­кратно исследованной задачи проиллюстрируем решение, полученное с помощью программы TORA.

Выходные результаты программы разбиты на два основных раздела: числовые ре­зультаты решения задачи и данные анализа чувствительности (раздел Sensitivity Analysis). В первом разделе представлены оптимальные значения переменных (первая таблица) и значение целевой функции (Objective value). В рассматриваемом примере оптимальное значение переменной x_t (количество выпускаемой краски для наружных работ) равно 3 т, а переменной х₂ (количество выпускаемой краски для внутренних работ) — 1,5 т. Соответственно, доход составляет 21 ООО долл. В следующей таблице данного раздела представлены ограничения (Constraint). В этой таблице показаны значения дополнительных переменных, остаточных (Slack-), избыточных (Surplus-I-) и значения правых частей неравенств (столбец RHS⁴).

Из таблицы видно, что значения дополнительных переменных для первых двух не­равенств равны нулю. Это означает, что сырье Ml и М2 потребляется полностью, без остатка. В третьем и четвертом ограничениях значения дополнительных пере­менных отличны от нуля, т.е. неравенства этих ограничений выполняются строго.

В верхней части раздела Sensitivity Analysis в двух таблицах показаны результаты анализа чувствительности при изменении по отдельности коэффициентов целевой

⁴ RHS — сокращение от Right Hand Side, т.е. "правая сторона". — Прим. перев.

Глава 2. Введение в линейное программирование

функции (первая таблица) и значений правых частей неравенств ограничений (вторая таблица). Например, текущее оптимальное решение сохраняется до тех пор, пока доход на тонну краски для внешних работ составляет от 2000 до 6000 долл. Текущее оптимальное решение также будет сохранено, если ежеднев­ные поступления сырья Ml будут находиться в пределах от 20 до 36 тонн. Такой же результат получен графическим способом в примерах 2.3.1 и 2.3.2.

Теперь рассмотрим информацию, приведенную в столбцах Reduced Cost (Приведенная стоимость) и Dual Price (Двойственная цена) таблиц раздела Sensitivity Analysis.

Начнем с приведенной стоимости. С точки зрения экономиста, переменные в моде­ли ЛП можно рассматривать как числовые характеристики интенсивности опреде­ленных видов деятельности (или процессов), в результате которых потребляются ресурсы ("вход" модели) в целях получения прибыли ("выход" модели). Из этой интерпретации вытекает следующее определение.

Если приведенная стоимость какого-либо процесса положительна, то отсюда следу­ет, что стоимость потребленных ресурсов больше возможного дохода (все на едини­цу интенсивности процесса), поэтому такой процесс экономически не приемлем. Это обусловливает нулевое значение соответствующей переменной в оптимальном решении. Если же экономически привлекательный процесс имеет нулевую приве­денную стоимость, то это означает, что достигнута точка равновесия, когда "выход" (единичный доход) равен "входу" (единичной стоимости ресурсов). В оп­тимальном решении, показанном на рис. 2.9, обе переменные х_х и х_г имеют положи­тельные значения и нулевые приведенные стоимости.

Приведенная стоимость на⁴} (Стоимость потребленных⁴} (Доход иа единицу⁴

ресурсов на единицу - интенсивности ^ интенсивности процесса у' J ^ процесса у ,

Теперь рассмотрим определение двойственной цены. Двойственная цена — это просто еще одно название стоимости единицы ресурсов, определенной в разде­ле 2.3.3. Она равна вкладу, который привносит в значение целевой функции изме­нение на одну единицу лимита, определяющего доступность ресурса. Термин "двойственная цена" произошел от названия "проблема двойственности" из тео­рии линейного программирования (см. главу 4). Для обозначения стоимости еди­ницы ресурсов такие термины, как теневая цена (shadow price) и симплексный мультипликатор (simplex multiplier), применяются значительно реже. Хотя назва­ние "стоимость единицы ресурсов", введенное в разделе 2.3.3, лучше отображает смысл, вкладываемый в это понятие, мы все же будем использовать термин "двойственная цена" (dual price), так как он применяется во всех коммерческих программах решения задач ЛП.

На рис. 2.9 видно, что двойственные цены для сырья Ml и М2 равны соответствен­но 0,75 и 0,50 (т.е. 750 и 500 долл.) за тонну. Такие же результаты получены гра­фическим способом в примере 2.3.3 и справедливы только при условии, что 20<М,<36 и 4<М₂<20/3 (здесь через М_х и М₂ обозначено количество сырья Ml иМ2 соответственно). Отсюда следует, что если, например, доступное количество сырья Ml возрастет от текущего уровня в 24 т до 28, то оптимальное значение целе­вой функции увеличится на 750 х (28 - 24) = 3000 долл. Но если доступное количе­ство сырья Ml возрастет до 40 т (т.е. выйдет за интервал осуществимости), необхо­димо искать новое оптимальное решение.

единицу интенсивности процесса j

2.4. Компьютерное решение задач ЛП

*** OPTIMUM SOLUTION SUMMARY ***

Title: Problem 2.5a-2

Final iteration No: 4

Objective value (max) =63000.0000

Variable	Value	Obj CoefF Obj Val Contnb
xl Juice	500.0000	18.0000 9000.0000
x2 Paste	6000.0000	9.0000 54000.0000
Constraint	RHS	Slack(-)/Surplus(+)

1 (<) 60000.0000 0.0000-

2(<) 2000.0000 1500.0000-

3 (<) 6000.0000 0.0000-

*** SENSITIVITY ANALYSIS *** Objective coefficients -- Single Changes:

Variable Current CoefF Min CoefF Max CoefF Reduced Cost

xl Juice 18.0000 0.0000 27.0000 0.0000

x2 Paste 9.0000 6.0000 infinity 0.0000

Right-hand Side - Single Changes:

Constraint Current RHS Min RHS Max RHS Dual Price

1 (<) 60000.0000 48000.0000 96000.0000 0.7500

2(<) 2000.0000 500.0000 infinity 0.0000

3(<) 6000.0000 1500.0000 7500.0000 3.0000

Objective Coefficients - Simultaneous Changes d:

Nonbasic Var Optimality Condition

sx3 0.7500+ 0.0417 dl >= 0

sx5 3.0000+ 1.0000d2+ -0.3333 dl >=0

Right-hand Side Ranging - Simultaneous Changes D:

Basic Var Value/Feasibilty Condition

x2 Paste 6000.0000+ 1.0000 D3>=0

xl Juice 500.0000 + 0.0417D1 + -0.3333 D3>=0

sx4 1500.0000+ -0.0417D1 + 1.0000 D2+ 0.3333 D3>=0

Рис. 2.9. Выходные результаты программы TORA

Глава 2. Введение в линейное программирование

Двойственные цены для третьего и четвертого ограничений в данной модели равны нулю при изменении значений правых частей этих неравенств от -1,5 до оо и от 1,5 до оо соответственно. Это означает, что ограничения, налагаемые рынком на струк­туру производства (ограничение на производство краски для внутренних работ до 2 т и т.п.), в данной ситуации не оказывают влияния на оптимальное решение.

2.4.2. Решение задач ЛП с помощью Excel

Покажем на модели Reddy Mikks, как надо располагать данные на рабочем лис­те, чтобы было удобно использовать средство Excel Поиск решения (файл рабочей книги ch2SolverReddyMikks.xls⁵). В верхней части рис. 2.10 показано табличное представление этой модели. Здесь содержится 4 типа данных:

1) входные данные (затененные ячейки В5:С9 и F6:F9),

2) значения переменных и целевой функции (ячейки в прямоугольнике B13:D13),

3) формулы, по которым вычисляются значения целевой функции и левых час­тей ограничений (ячейки D5:D9) и

4) поясняющие заголовки и надписи.

-_£=В5*В$13+С5*С$13

Б С Р~1 Е ' Модель Reddy Mikks

Всего Ограничении

ОПТ

Поиск решения

□ Установить целевую ячейку:

Равной: <!" максимальному значению

<** минимальному значению Изменяя ячейки:

<~ значению:

Выполни!

Закрыт-

 

|$В$13 $С$13		Предположить
Ограничения:
]$В$13:$С$13 >= 0 KD$6:$D$9 <= $F$6:$F$9	J	Добавить Изменить
	zl	Удалить

Параметр!

Boccjart Га

-1

Сгр

Рис. 2.10. Решение задачи ЛП в Excel

Для средства Поиск решения требуется информация только первых трех типов — поясняющие заголовки и надписи необходимы только для того, чтобы сделать таб-

⁶ Рабочие книги Excel, которые упоминаются в первых девяти главах, русифицированы и содержатся на прилагаемом к книге компакт-диске. Их названия совпадают с названиями исходных файлов, перед которыми стоит слово "Копия". Например, русифицированный ва­риант данной рабочей книги имеет название Копия ch2SolverReddyMikks.xls. — Прим. ред.

2.4. Компьютерное, решение задач ЛП

личное представление модели более понятным и удобочитаемым. Относительное расположение ячеек, содержащих информацию разных типов, не обязательно должно быть таким, как показано на рис. 2.10. Например, ячейки, содержащие зна­чения переменных и целевой функции, не обязательно должны располагаться в од­ном непрерывном диапазоне ячеек или внизу таблицы — часто их размещают в верх­ней части табличной модели. Важно только то, чтобы они находились в отдельных ячейках и на них можно было бы сослаться при задании параметров средства Поиск решения. Вместе с тем мы рекомендуем придерживаться структуры табличной моде­ли, как показано на рис. 2.10, поскольку она наглядна и удобна в работе.

Покажем соответствие между математической моделью и табличной. Начнем с соответствия формул этих моделей. Коэффициенты целевой функции и левых частей ограничений помещены в диапазон ячеек В5:С9. В следующей таблице при­ведены алгебраические формулы и эквивалентные им формулы Excel и ячейки, в которых эти формулы записаны.

	Алгебраическая формула	Формула Excel	Ячейка
Целевая функция z	5xi +4хг	=В5*В$13+С5*С$13	D5
Ограничение 1	6X1 + 4X2	=В6*В$13+С6*С$13	D6
Ограничение 2	Xi + 2X2	=В7*В$13+С7*С$13	D7
Ограничение 3	- Х1 + Х2	=В8*В$13+С8*С$13	D8
Ограничение 4	0X1 + Х2	=В9*В$13+С9*С$13	D9

Отметим, что вы должны ввести формулу только в ячейку D5, а затем ее надо скопировать в ячейки D6:D9. Чтобы правильно скопировать формулы, в формуле ячейки D5 надо ссылки на ячейки В13 и С13 (содержащих значения х_х и х₂) сделать абсолютными в виде $В$13 и $С$13. Для больших табличных моделей в ячейку D5 можно ввести формулу

= СУММПРОИЗВ(В5:С5;$В$13:$С$13) и затем скопировать ее в ячейки D6:D9.

После ввода исходных данных и расчетных формул табличная модель готова для использования средства Поиск решения. В меню Сервис выберите команду Поиск решения. Откроется одноименное диалоговое окно, показанное на рис. 2.10. В этом окне надо ввести адрес ячейки, в которой вычисляется значение целевой функции, указать, надо ли минимизировать или максимизировать целевую функ­цию, и ввести адреса ячеек, содержащих значения переменных. В нашей модели:

в поле ввода Установить целевую ячейку вводится D5;

устанавливается переключатель Равной максимальному значению;

в поле ввода Изменяя ячейки вводится $В$13:$С$13.

Эта информация указывает средству Поиск решения, что переменные находятся в ячейках В13 и С13, и надо найти максимум целевой функции, значение которой вычисляется в ячейке D5.

Далее надо задать ограничения модели, щелкнув на кнопке Добавить в диало­говом окне Поиск решения. Отрывшееся диалоговое окно Добавление ограничения предоставляет средства для ввода всех частей ограничений (левой части, знака неравенства и значения правой части). Используя это окно, вводим ограничения модели в таком виде.

$D$6:$D$9<=$F$6:$F$9

Глава 2. Введение в линейное программирование

Напомним, что в ячейках F6:F9 записаны значения правых частей ограничений. Теперь осталось ввести ограничения неотрицательности для переменных. С по­мощью диалогового окна Добавление ограничения вводим

$В$13:$С$13>=0

Когда Поиск решения найдет решение данной задачи, оптимальное значение це­левой функции появится в ячейке D5, а значения переменных х_х и х₂ — в ячейках В13 и С13 соответственно. Для удобства мы используем ячейку D13 для отображе­ния значения целевой функции (в эту ячейку введена формула =D5) — в этом слу­чае все элементы оптимального решения отображаются рядом в одной строке.

Теперь все готово для решения нашей задачи, достаточно щелкнуть на кнопке Выполнить в диалоговом окне Поиск решения. Но перед этим желательно проверить установленные параметры работы средства Поиск решения (максимальное время поиска решения, максимальное количество итераций, относительная погрешность и т.д.), для чего надо открыть диалоговое окно Параметры поиска решения, щелк­нув на кнопке Параметры. Самое важное — установить опцию Линейная модель. В этом же окне можно указать, что все переменные должны быть неотрицательны­ми (опция Неотрицательные значения).⁶

Если табличная модель создана правильно, то решение появится в выходных ячейках табличной модели (в нашем случае в ячейках B13:D13). Также появится новое диалоговое Результаты поиска решения, которое даст возможность получить более детальную информацию о решении в виде отчетов, включая важный отчет по устойчивости. Эти отчеты формируются на отдельных листах рабочей книги. На рис. 2.11 показан отчет по устойчивости для модели Reddy Mikks. Информация в этом отчете полностью совпадает с той, что предоставляет программа TORA, и ин­терпретируется аналогичным образом. Заметим, что здесь теневая цена — то же самое, что dual price (двойственная цена) в отчете программы TORA.

Необходимо подчеркнуть, что описанная табличная модель Reddy Mikks по­строена и решена "прямолинейно". Другие модели могут потребовать определен­ных ухищрений и преобразований для того, чтобы к ним можно было применить средство Поиск решения. Один класс таких моделей ЛП, а именно сетевых моделей, будет рассмотрен в главе 6.

2.4.3. Решение задач ЛП с помощью LINGO и AMPL

Модели ЛП, представленные в этой книге, вынужденно упрощены и минимизиро­ваны. В реальной жизни модели ЛП могут содержать тысячи переменных и ограни­чений. В этом случае соответствующие данные хранятся во внешних файлах, а сами данные могут быть извлечены из какой-либо базы данных или подготовлены в элек­тронных таблицах. При этом данные для больших моделей обычно представляются в матричной форме в виде чрезвычайно больших числовых массивов. В таком слу­чае вводить данные с помощью Excel или TORA непрактично, кроме того необхо­димы средства для автоматического генерирования моделей на основе этих данных.

Для выполнения таких задач существует несколько коммерческих программ­ных пакетов, среди которых назовем AMPL, GAMS, LINGO и MPL. Основная идея

Необходимо предостеречь от некоторых "причуд" средства Поиск решения. Если вы за­дадите слишком малое значение Относительная погрешность (например, 0,000000001), то можете получить странное сообщение, что для вашей модели не выполняются предположе­ния о линейности. Также вследствие округления значений в выходных отчетах можно полу­чить не совсем точные значения (например, 1Е-14 вместо 0 или 9,999999999999 вместо 10).

2.4. Компьютерное решение задач ЛП

построения этих пакетов заключается в том, чтобы иметь готовую пустую алгеб­раическую модель ЛП и затем на основе предоставляемых данных сформировать конкретную модель. Эти данные могут быть встроены в модель либо могут считы-ваться из внешних файлов и из файлов электронных таблиц. Это делает модель ис­ключительно гибкой, позволяя настраивать ее под те или иные данные.

А В С D Е 1 _, Microsoft Excel 10.0 Отчет по устойчивости 2 s Рабочий лист: [ch2SolverReddyMikks.xlsJJlHCTl	F	G	Н '_ |Г
а ! 5 1 Изменяемые ячейки
6 i Результ. Нормир. Целевой Допустимое Допустимое 7 Ячейка Имя значение стоимость Коэффициент Увеличение Уменьшение
8 . $В$13 Решение х1 3 9 i $С$13 Решение х2 1,5	0 0	5 4	1 6	3 , 0,666666667
щ : .11 [Ограничения
_12_ Результ. 13 Ячейка Имя значение	Теневая Цена	Ограничение Правая часть	Допустимое Увеличение	Допустимое Уменьшение
J4_ $D$6 Сырье М1 Всего 24 15 $D$7 Сырье М2 Всего 6 •18- $D$8 Спрос 1 Всего -1,5 '17'; $D$9 Спрос 2 Всего 1.5	0,75 0,5 0 0	24 6 1 2	0,666666667 1Е+30 1Е+30	4 2 2,5 0.5
-ТО - -, , И « -» МЛ Отчет по устойчивости 1 / Лист! /		Ы		I мг

Рис. 2.11. Отчет по устойчивости

В этом разделе кратко опишем два популярных пакета решения задач оптими­зации: LINGO и AMPL. Это описание по понятным причинам не будет очень под­робным и всесторонним, но, вместе с тем, даст общее представление о том, как ра­ботают эти пакеты. Оба этих пакета имеют специальные обучающие версии, которые можно загрузить с Web-узлов www. lingo. com и www. ampl. com.

Моделирование в LINGO. На рис. 2.12 показан листинг модели Reddy Mikks, созданный в LINGO (файл ch.2LingoReddyMikks.lng). В этом листинге служебные слова LINGO записаны прописными буквами и выделены полужирным начертани­ем (на самом деле язык LINGO не чувствителен к регистру символов), остальные элементы листинга записаны пользователем.

В листингах LINGO строки, начинающиеся с восклицательного знака, являются комментариями и игнорируются процессором LINGO. Все стандартные операторы, включая комментарии, должны заканчиваться точкой с запятой. Служебные слова MODEL, SETS и DATA должны заканчиваться двоеточием, однако служебные слова END, ENDSETS и ENDDATA (закрывающие операторные скобки) не требуют в конце каких-либо знаков препинания.

В модели на рис. 2.12 входные данные содержатся внутри модели, что не удоб­но, если необходимо найти решение одной и той же модели для разных исходных данных. Ниже мы покажем, как можно выйти из этой ситуации путем сохранения данных в отдельных внешних файлах.

Оператор TITLE предваряет название модели. В операторных скобках SETS: ENDSETS пользователем вводятся имена основных компонентов модели ЛП — ог­

Глава 2. Введение в линейное программирование

раничений, переменных и матрицы, содержащей коэффициенты функций огра­ничений. Важно отметить, что эти данные определяются пользователем до нача­ла использования модели. На рис. 2.12 видно, что мы использовали имена Constr (Ограничения), Var (Переменные) и ConsVar(Constr,Var) (это массив коэффици­ентов, размерности ConstrxVar). Конечно, вы можете использовать любые другие

Шодель Reddy Mikks - данные внутри модели; MODEL:

TITLE Reddy mikks model;

I--------------------алгебраическое определение модели ЛП;

SETS:

Constr: Rhs; Var: С, X;

ConsVar (Constr, Var) : Aij ; EHDSETS

1------------------------------------построение модели;

MM-esUM( Var(j) : C(j)*X(j) ); ! целевая функция;

SFOR( Ограничения; Constr (i) : SSUM( Var (j) : Aij (i, j ) *X (j) )<=Rhs (i) ) ;

i------------------------------------данные для модели;

DATA:

Constr = Ml M2 Demandl Demand2; Rhs = 24 6 1 2; Var = XI X2; С = 5 4; Aij =64

1 2

-1 1

0 1;

E HDD AT A END

Рис. 2.12. Листинг LINGO модели Reddy Mikks

имена по вашему выбору. Ограничения имеют числовые значения правой части, вектор этих значений назовем Rhs (от Right-hand side — правая часть). Отношение между ограничениями и их правыми частями задается оператором Constr: Rhs; Аналогично оператор Var: С, X;

указывает, что каждой переменной X соответствует в целевой функции коэффици­ент С (X и С — векторы). Наконец, матрица, содержащая коэффициенты функций ограничений, названа Aij с помощью оператора

ConsVar(Constr,Var): Ai j ;

Теперь заданы все элементы, необходимые для построения алгебраической мо­дели. Используя фиктивный индекс j для представления переменной у, целевая функция строится как

MAX=@SUM( Var(j): C(j)*X(j) );

Этот оператор задает целевую функцию как сумму произведений C(j)*X(j), причем сумма берется по всем элементам множества Var(j). Ограничение i строится сле­дующим образом:

Constr(i):@SOM( Var(j): Aij(i,j)*X(j) )<=Rhs(i)

2.4. Компьютерное решение задач ЛП

Для вычисления всех ограничений из множества Constr(i) используется цикл

@FOR(Constr(i):

@SUM( Var(j): Aij(i,j)*X(j) )<=Rhs(i) ) ;

Отметим, что тело цикла @FOR ограничивается круглыми скобками.

Последний раздел листинга на рис. 2.12 содержит данные, подставляемые в ал­гебраическую модель. Так, множество Constr определяется как множество из четы­рех ограничений, названных Ml, М2, Demandl и Demandl (Cnpocl и Спрос2). От­метим обязательные пробелы между именами — по их числу определяется количество элементов в множестве. В следующей строке вектору Rhs присваивают­ся значения правых частей ограничений 24, 6, 1 и 2. Элементам множества Var обычно даются имена XI и Х2 (если модель имеет только две переменные). Соот­ветственно, С присваиваются два элемента, 5 и 4, значения коэффициентов целевой функции. Наконец, массиву Aij присваиваются значения коэффициентов левых частей ограничений в соответствии с определением множества ConsVar(Constr,Var). Не обязательно помещать элементы каждого ограничения в отдельной строке, как в листинге на рис. 2.12. Здесь это сделано для удобства чтения.

По умолчанию в LINGO предполагается, что все переменные неотрицательны. Свободные переменные (т.е. такие, которые могут принимать как положительные, так и отрицательные, значения) задаются с помощью оператора @FREE. Например, если Х2 — свободная переменная, то в модели она должна быть описана оператором @FREE(X(2));

Этот оператор можно вставить в любое место листинга после оператора ENDSETS, даже в оператор цикла.

Стандартный выходной результат работы программы LINGO представлен на рис. 2.13. Оптимальное решение записано как Х(Х1) = 3 и Х(Х2) = 1.5 со значением целевой функции 21. В нижней части выходного отчета выводится список значе­ний дополнительных переменных для каждого ограничения (строки 2- 5) вместе с соответствующими двойственными ценами (столбец Dual Prices). В строке 1 при­ведено значение целевой функции. Остальные значения в выходном отчете повто­ряют входные данные модели.

Выходной отчет программы LINGO можно настраивать, выводя только необхо­димые данные. Отметим, что в этот отчет не включаются автоматически результа­ты анализа чувствительности оптимального решения. Вместе с тем LINGO предос­тавляет возможности проведения такого анализа и вывода его результатов.

Мощность и гибкость таких программ, как LINGO, заключается в том, что входные данные модели не обязательно должны быть включены непосредственно в модель, как это сделано в листинге на рис. 2.12. Входные данные могут находить­ся во внешних файлах. На рис. 2.14 показан листинг модели Reddy Mikks, где с по­мощью оператора @FILE присоединяются два внешних файла. Содержимое этих файлов показано на рис. 2.15. Таким образом, заменяя эти файлы другими, можно просчитывать модель для разных входных данных.

Моделирование в AMPL. Используем ту же модель Reddy Mikks для описания работы программы AMPL. На рис. 2.16 показан листинг этой модели, созданный в AMPL (файл ch2AmplReddyMikks.mod). Как и в примере LINGO, служебные сло­ва AMPL здесь выделены полужирным шрифтом.

Первым в листинге стоит оператор set, определяющий ограничения и перемен­ные модели с помощью задаваемых пользователем имен Constr и Var (мы сохранили здесь имена из модели LINGO для того, чтобы можно было сравнить модели

Глава 2. Введение в линейное программирование

в LINGO и AMPL). Далее с помощью оператора param задаются имена элементов целевой функции и ограничений. Так, С определяет коэффициенты целевой функ­ции как функция множества Var. Rhs определяет значения правых частей ограни­чений как функция множества Constr, a Aij — коэффициенты левых частей ограничений как функция множеств Constr и Var.

Global optimal solution found at step: 4 Objective value: 21.00000

Model Title: REDDY MIKKS MODEL

Variable		Value	Reduced Cost
RHS (	Ml)	24.			.000000
RHS (	M2)		.00000		.000000
RHS( DEMAND1)	1.	.00000	0.	.000000
RHS( DEMAND2)	2.	,00000	0.	.000000
C(	XI)	5.	,00000	0,	,000000
C(	X2)	4.	.00000	0,	,000000
X(	XI)	3.	,00000	0,	.000000
X(	X2)	1.	,50000	0.	.000000
AIJ( Ml,	XI)	6.	,00000	0.	.000000
AIJ( Ml,	X2)	4.	,00000	0,	.000000
AIJ( M2,	XI)	1.	,00000	0.	.000000
AIJ( M2,	X2)	2.	,00000	0.	.000000
AIJ( DEMAND1,	XI)	-1.		0.	.000000
AIJ( DEMAND1,	X2)	1.	,00000	0,	,000000
AIJ( DEMAND2,	XI)	0.000000	0.	.000000
AIJ( DEMAND2,	X2)	1.		0.	.000000
Row	Slack oc Surplus	Dual Pcice
	21.0000	1.00000
	0.000000	0.750000
	0.000000	0.500000
	2.50000	0.000000
	0 . 500000	0.000000

Рис. 2.13. Выходной отчет программы LINGO

!Модель Reddy Mikks - входные данные во внешних файлах; MODEL:

TITLE Reddy mikks model;

1--------------------алгебраическое определение модели ЛП;

SETS :

Constr: Rhs;

Vac: С, X;

ConsVar(Constr,Van): Aij; ENDSETS

i------------------------------------построение модели;

MAX=@SUM( Vac (j) : C(j)*X(j) ); !целевая функция;

SFOR ( Ограничения; Constc(i) :@SUM( var(j) : Aij <i, j) *X(j) )<=Rhs(i) ) ;

i------------------------------------данные для модели;

DATA:

Constr=@FIL,E(ch2LingoFldata.lng) ; !чтение из файла; Rhs = 24 б 1 2; Vac = XI Х2; С = 5 4;

Aij=@FILE (ch2LingoFldata.lng) ; !чтение из файла; EHDDATA END

Рис. 2.14. Листинг LINGO модели Reddy Mikks с внешними файлами

2.4. Компьютерное решение задач ЛП

!........содержимое 1-го внешнего файла;

Ml М2 Demandl Demand2

!........ содержимое 1-го внешнего файла;

6412-1101

Рис. 2.15. Содержимое внешних файлов для модели Reddy Mikks

#-------------------------------определение множеств модели

set Constr; #множество ограничений

set Var; #множество переменных

#----------------------------задание имен элементам модели

param С (Var); коэффициенты целевой функции

param Rhs (Constr) ; #правые части ограничений

param Aij (Constr, Var); #коэфф. левых частей ограничений

#------------------------------------задание переменных

var X (Var) >= 0; #условие неотрицательности

#------------------------------------задание модели

maximize Total: sum (j in Var) C[j]*X[j]; #целевая функция Subject to Restrictions (i in Constr) : Ограничения sum (j in Var) Aij [i, j]*X[ j] <= Rhs[i];

#------------------------------------данные для модели

data,

set Constr := Ml M2 Demandl Demand2; set Var := XI X2;

рагаж Rhs	: =
	Ml
	M2
	Demandl
	Demand2	2;
param Aij	: =
	Xl	X2
Ml
M2
Demandl	-1
Demand2		1;
param С :=	= XI 5 X2	4;

Puc. 2.16. Листинг AMPL модели Reddy Mikks

Далее оператор var задает имя X (имя определяется пользователем) для пере­менных множества Var. В отличие от программы LINGO, где все переменные по умолчанию предполагаются неотрицательными, в AMPL все переменные изна­чально предполагаются свободными. В модели Reddy Mikks переменные ограничи­ваются условием неотрицательности, поэтому добавляется вы