Output Summary

14 'Av. facility utilization = 15]Percent idleness (%) =

16 /laximum queue length:

17 «v queue length, Lq =

18 iAv nbr in system, Ls =

19 Av queue time. Wq = Й A« ■system time, Ws =

21 'Sum(ServiceTime) -

22 Sum(Wq) =

23Sum(Ws)=_

0 92 7.92

1 13

2 05 15.33 •?-! B7

250 75 306 63 557 38

Press F9 to

trigger a

new simulation run

Nbr llnterArvlTirrServiceTime ArrvlTime DeparfXime,	Wq	Ws
	5 53	10.83	0 00	10.83	0.00	10.83
	14 32	10 35	5.53	21.19	5 30	15.66
	25 87	12.66	19.85	33.85	1 34	14 00
	1 63	12 11	45 72	57 83	0.00	12 11
	4 18	12.541	47.35	70 37	10 48	23.02
	6.91	12 86	51.53,	83.23	18 84	31 70
	4 84	12.08	58 43	95.30	24.79	36 87
	22 12	10.18	63 27	105 48	32.03	42 21
	1 86	13 18	85.39	118.67	20 09	33 28
	20 41	14.98	87.25	133.65	31.42	46 40
	6 47	13.41	107 66	147 06	25.99	39.40
	10.82	14 12	114.13!	161 17	32.93	47 04
	11.50	12.32	124.95	173.50	36.22	48 54
	43 87	14.67'	136 45	188 16	37.04	51.71
		13.62'	180.32	201 78	7.84	21.46
	10.15		196.13	215.25	5.65
	15.23	13.96	206.28	229 21	8.96	22 93
	18 58	10.88	221.51	240 09	7.70	18 58
	21 65	11.97)	240.10	252.06	0 00	11 97
	13.62	10.561	261.75	272.31	0 00	10 56

Рис. 18.9. Результаты имитации модели с одним сервисом в Excel

В шаблоне каждому поступлению клиента в систему соответствует одна строка. Время между поступлениями и время обслуживания для каждого клиента гене­рируются на основе исходных данных. Предполагается, что первое поступление

18.5. Механика дискретной имитации

происходит в момент времени Т = 0. Поскольку средство обслуживания в начале работы свободно, то первый клиент обслуживается сразу. Поэтому

(время ухода клиента 1) = (время прихода клиента 1) 4- (время сюслуживания клиента 1) =

= 0+ 14,35 = 14,35,

(время прихода клиента 2) = (время прихода клиента 1) + (время между прихо­дами клиентов) = = 0+ 15,15= 15,15.

Для определения времени ухода других клиентов i используется следующая формула:

(время ухода^ (время прихода^ (время ухода^ j (время обслуживания^

^ клиента; J Н клиента/ )' у клиента /-lj] ^ клиента/

Из формулы видно, что клиент не может быть обслужен, пока сервис не освобо­дится. Итак, из формулы и рис. 18.9 видно, что

время ухода клиента 3 = тах{18,89, 26,41} + 14,86 = 41,25.

Теперь обратим внимание на то, как формируются статистические данные мо­дели. Сначала заметим, что для клиента i время ожидания в очереди W (I) и время пребывания в системе W_s(i) вычисляется по таким формулам:

время ухода^ (время прихода⁴] (время обслуживания ^ клиента / J ^ клиента / J ^ клиента /

^ (время ухода⁴ время прихода^ ^ клиента / ) клиента / )

Может показаться, что для вычисления оставшихся статистических данных имитации модели необходимо отслеживать изменения в использовании сервиса и длины очереди, как это делалось в разделе 18.5.1. Но, применяя формулы, при­веденные в конце раздела 18.5.1 (объяснение к которым дано на рис. 18.8), вычис­ления можно упростить, если использовать следующие соотношения.

1. Область под кривой использования сервиса = сумма времени обслуживания всех клиентов.

2. Область под кривой длины очереди = сумма времени ожидания всех клиентов.

Для использования этих соотношений вычисляется три суммы (ячейки Е21:Е23 на рис. 18.9):

сумма времени обслуживания = 248,66,

сумма значений W = 513,14,

сумма значений W_t = сумма значений W_q + сумма времени обслуживания = = 761,80 (= 248,66 + 513,14).

Поскольку последний клиент (клиент 20) ушел в момент времени Т = 252,64, следовательно

среднее время использования сервиса = 248,66/252,64 = 0,9842, средняя длина очереди = 513,14/252,64 = 2,03,

среднее время простоя сервиса, выраженное в процентах, вычисляется как

(1 - 0,9842) х 100 = 1,575 %. Остальные статистические данные вычисляются обычным образом.

Глава 18. Имитационное моделирование

Среднее время ожидания в очереди = сумма значений W^/число клиентов =

= 513,14/20 = 25,66.

Среднее время пребывания в системе = сумма значений И^/число клиентов =

= 761,81/20 = 38,09.

Максимальное количество клиентов, генерируемое шаблоном, не должно пре­вышать 500.

Еще одна рабочая книга разработана для имитации моделей с несколькими сер­висами (файл chl8MultiServerSimulator.xls). Вычисления в ней выполняются на той же теоретической основе, что и при использовании моделей с одним сервисом. Тем не менее определить время ухода клиентов в этой ситуации более сложно, для чего используются макросы VBA.

УПРАЖНЕНИЯ 18.5.2

1. Используя исходные данные из раздела 18.5.1, выполните в Excel имитацию 10 поступлений клиентов и постройте график изменения использования сер­виса и длины очереди как функцию от времени имитации. Проверьте, что площади под соответствующими кривыми равны сумме времени обслужива­ния и сумме времени ожидания.

2. Имитируйте модель типа М/М/1 для 500 поступлений при условии, что интен­сивность поступлений X равна 4 клиентам в час и интенсивность обслуживания ц составляет 6 клиентов в час. Повторите имитацию 5 раз (обновив значения на рабочем листе нажатием клавиши <F9>) и определите 95%-ные доверитель­ные интервалы для всех полученных оценок показателей работы модели.

3. Комплектующие для телевизоров поступают по конвейеру каждые 11,5 мин. для проверки на испытательном стенде, обслуживаемом одним оператором. Детальная информация по работе испытательного стенда недоступна. Тем не менее, по оценке оператора, он тратит "в среднем" 9,5 мин. на проверку од­ной детали. В наихудшем случае время проверки не превышает 15 мин., а для некоторых комплектующих время проверки составляет менее 9 мин.

a) Используйте шаблон Excel для имитации проверки 200 комплектующих для телевизоров.

b) На основе 5 имитаций оцените среднее число комплектующих, ожидаю­щих проверки, и среднее время использования испытательного стенда.

18.6. МЕТОДЫ СБОРА СТАТИСТИЧЕСКИХ ДАННЫХ

Имитационное моделирование представляет собой статистический эксперимент. Его результаты должны основываться на соответствующих статистических про­верках (с использованием, например, доверительных интервалов и методов про­верки гипотез). Для выполнения этой задачи получаемые наблюдения и имитаци­онный эксперимент должны удовлетворять следующим трем требованиям.

1. Наблюдения имеют стационарные распределения, т.е. распределения не из­меняются во время проведения эксперимента.

2. Наблюдения подчиняются нормальному распределению.

3. Наблюдения независимы.

18.6. Методы сбора статистических данных

Иногда на практике результаты имитационного моделирования не удовлетво­ряют ни одному из этих требований. Тем не менее их выполнение гарантирует на­личие корректных способов сбора наблюдений над имитационной моделью.

Рассмотрим сначала вопрос о стационарности распределений (первое требова­ние). Результаты наблюдений над моделью зависят от продолжительности периода имитации. Начальный период неустойчивого поведения модели (системы) обычно называется переходным. Когда результаты имитационного эксперимента стабили­зируются, говорят, что система работает в установившемся режиме. Продолжи­тельность переходного периода определяется в значительной степени начальными характеристиками модели, и невозможно предсказать, когда наступит установив­шийся режим. В общем случае, чем длиннее продолжительность прогона модели, тем выше шанс достичь установившегося состояния.

Рассмотрим теперь второе требование, состоящее в том, что наблюдения над имитационной моделью должны иметь нормальное распределение. Это требование можно выполнить, если привлечь центральную предельную теорему (см. раз­дел 12.4.4), утверждающую, что распределение среднего выборки является асим­птотически нормальным независимо от распределения генеральной совокупности, из которой взята выборка. Центральная предельная теорема, таким образом, есть главное средство удовлетворения требования о нормальности распределения.

Третье требование касается независимости наблюдений. Природа имитационного эксперимента не гарантирует независимости между последовательными наблюде­ниями над моделью. Однако использование выборочных средних для представле­ния отдельных наблюдений позволяет смягчить проблему, связанную с отсутстви­ем независимости. Для этого, в частности, следует увеличивать интервал времени имитации для получения выборочного среднего.

Понятия переходного и установившегося состояний имеют силу в ситуациях, именуемых незаканчивающейся имитацией, т.е. имитацией, применяемой к сис­темам, которые функционируют бесконечно долго. При заканчивающейся имита­ции (например, работа банка, если он обычно работает восемь часов в день) пере­ходное поведение является частью нормального функционирования системы и, следовательно, не может игнорироваться. Единственным выходом в такой ситуа­ции является увеличение, насколько это возможно, числа наблюдений.

Обсудив "подводные камни" имитационного эксперимента и средства, с помо­щью которых их можно обойти, рассмотрим теперь три наиболее общих метода сбора информации в процессе имитационного моделирования: метод подынтерва­лов, метод повторения и метод циклов.

18.6.1. Метод подынтервалов

На рис. 18.10 проиллюстрирована идея метода подынтервалов. Предположим, что имитация длится на протяжении Т единиц времени (т.е. длина прогона моде­ли равна Т) и требуется получить п наблюдений. В соответствии с методом по­дынтервалов необходимо сначала "обрезать" информацию, относящуюся к пере­ходному периоду, а затем разделить остаток результатов имитации на п равных подынтервалов (групп). Среднее значение искомой величины (например, длины очереди или времени ожидания в очереди) внутри каждого подынтервала исполь­зуется затем в качестве единственного наблюдения. Отбрасывание начального переходного периода означает, что статистические данные, собранные на протя­жении этого периода, не используются.

Глава 18. Имитационное моделирование

Преимущество данного метода состоит в том, что влияние переходных (нестационарных) условий уменьшается, в частности, на те данные, которые соб­раны в конце времени имитации. Недостаток заключается в том, что последова­тельные группы с общей границей являются коррелированными, что приводит к невыполнению предположения о независимости. Влияние корреляции может быть уменьшено путем увеличения интервала времени для каждой группы.

Переходный

период Группа 1 Группа 2

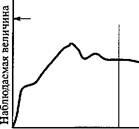
Группа п

Время имитации

Рис. 18.10. Иллюстрация к методу интервалов

Пример 18.6.1

На рис. 18.11 показано изменение длины очереди в системе обслуживания с одним сервисом (модель простой очереди) как функции времени. Период имитации со­ставляет Т= 35 часов, а длина переходного периода оценивается в 5 часов. Необхо­димо получить 5 наблюдений, т.е. п = 5. Соответствующая длина интервала времени для каждой группы равна (35 - 5)/5 = 6 часов.

Длина

очереди Q

Переходный
период | Группа 1 _ Группа 2	, Группа 3 ,	Группа 4	Группа 5 ,
~*--Н**-* _ ._,J L ^2='оГ	т*-»1 |Lj3=n	**-** А4=6Г>	**-Н
1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1	|.....1	_1 . 1 Г. . 1	Л5=15Ц 1 1 1 1 1 1

J_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I_I

5 10 15 20 25 30 35

Время имитации Рис. 18.11. Изменение длины очереди

Пусть g представляет среднюю длину очереди в группе /'. Так как длина очереди является переменной, зависящей от времени, то

Q,=—, / = 1,2, ...,5, t

где А-, — площадь под кривой длины очереди, t — длина интервала времени для группы. В рассматриваемом примере t = 6 часов.

18.6. Методы сбора статистических данных 729

Анализ данных, приведенных на рис. 18.11, приводит к следующей таблице.

Наблюдение/
А
а	2,33	1,67	1,83	1,00	2,5
Выборочное среднее	= 1,87		Выборочная дисперсия = 0,35

Выборочные среднее и дисперсию можно использовать, если это необходимо, для вычисления доверительного интервала.

Вычисление выборочной дисперсии в этом примере основано на использовании следующей хорошо известной формулы:

5>.-*)²

Эта формула является лишь приближением точного значения дисперсии, так как не учитывает эффекта автокорреляции между последовательными группами. Точ­ную формулу можно найти в работе [2].

18.6.2. Метод повторения

В данном методе каждое наблюдение представляется независимым прогоном (имитацией) модели, в котором переходный период не учитывается, как показано на рис. 18.12. Вычисление средних величин выборки для каждой группы прово­дится точно так, как и в методе подынтервалов. Единственное отличие в том, что в данном случае стандартная формула для дисперсии применима, так как группы не коррелированы между собой.

Преимуществом этого метода является то, что каждый имитационный прогон модели определяется своей последовательностью случайных чисел из интервала [О, 1], что действительно обеспечивает статистическую независимость получаемых наблюдений. Недостаток состоит в том, что все наблюдения могут оказаться под сильным влиянием начальных переходных условий. Этот недостаток можно смяг­чить, увеличив длину прогона модели.

Группа п

Т Т

Рис. 18.12. Иллюстрация к методу повторения

Глава 18. Имитационное моделирование

18.6.3. Метод циклов

Этот метод можно рассматривать как расширенный вариант метода подынтер­валов. Мотивацией данного метода является попытка уменьшить влияние авто­корреляции, которая характерна для метода подынтервалов, путем выбора групп таким образом, чтобы обеспечить одинаковые начальные условия для каждой из них. Например, если в качестве переменной рассматривается длина очереди, то каждая группа должна начинаться в тот момент, когда длина очереди равна нулю. В отличие от метода подынтервалов, в методе циклов длины интервалов каждой группы могут оказаться различными.

Хотя метод циклов и позволяет уменьшить влияние автокорреляции, его недос­татком является меньшее, по сравнению с методом подынтервалов, число получае­мых наблюдений при заданной длине прогона модели. Это следует из того, что нельзя заранее сказать, когда новая группа (цикл) начинается, и какова продолжительность каждого цикла. Однако можно ожидать, что в стационарных условиях начальные точки последовательных циклов будут расположены более или менее равномерно.

Вычисление среднего для цикла i в рассматриваемом методе определяется в ви­де отношения двух случайных величин а, и т.е. в виде х_: = ajb_r Определение ве­личин а₍ и Ъ_: зависит от вычисляемой переменной. Например, если переменная яв­ляется функцией времени, то а, представляет площадь под кривой, а Ь₍ — длительность соответствующего интервала времени. Если же переменная является функцией количества событий, то a_t — общая сумма наблюдений этой величины в пределах цикла i, а Ь_{ — общее число событий внутри соответствующего цикла.

Так как x_t является отношением двух случайных величин, можно показать, что в данном случае несмещенная оценка выборочного среднего определяется формулой

±У. п

где

па (п-)(па-а,)

)',=-=----=--, / = 1,2,

b nb -b_:

а=^—, Ь=^—. п п

В этом случае доверительный интервал для математического ожидания можно найти с помощью выборочного среднего у и стандартного отклонения величин y_t.

Пример 18.6.2

На рис. 18.13 показано число занятых обслуживающих устройств в одноканальной сис­теме обслуживания с тремя параллельными обслуживающими устройствами. Длина периода имитации — 35 единиц времени, а длина переходного периода — 4 единицы времени. Требуется оценить среднее значение использования сервисов методом циклов.

После отбрасывания переходного периода получаем четыре цикла, общей характе­ристикой начала каждого из которых является незанятость всех трех обслужи­вающих устройств. Результаты вычислений приведены в следующей таблице.

18.6. Методы сбора статистических данных

Занятость Переходный оборудования / период

	/ Группа]	Группа 2 Группа 3	Группа 4
3 2 1	• 1111111! 1	,I!i!I I i i! !!I i.
	5 10	15 20 25	30 35
		Время имитации
Рис. 18.13. Изменение количества занятых сервисов как функция времени
Цикл ;	а,	bi

а =8,5

Ъ =7,75

Вычисление_у, проводится в соответствии со следующей формулой:

4x8,5 (4-1)(4х8,5-а,) , ,_Л 102-За,

у, =----—-— = 4,39--'-.

7,75 4x7,75-/5, 31-6,

Эти вычисления выполняет шаблон Excel chl8Regenerative.xls, показанный на рис. 18.14.

	А I В	С	D		" E 1
	Regenerat	ive (Cycles) Method
	Input Data	_Output Results
	No. Batches __4
	•i bi
	12 9	1.3870968	i-		8 5000
	6 6	1 1563275	N	7 7500
	10 10	i 0.9585253	Average yi =	1.0973
В	6 7	0 8870968	Std Dev yi =	0 2243

Рис. 18.14. Вычисление в Excel задачи примера 18.6.2

УПРАЖНЕНИЯ 18.6

1. В примере 18.6.1 используйте метод подынтервалов для вычисления среднего времени ожидания в очереди для тех клиентов, которые вынуждены ожидать.

2. Пусть в имитационной модели используется метод подынтервалов для вы­числения средних величин в циклах. Переходный период — 100 единиц времени, длина каждого цикла также составляет 100 единиц времени. Ис­пользуя приведенные ниже данные, которые представляют время ожидания клиентов, как функцию времени имитации, определите 95%-ный довери­тельный интервал для среднего времени ожидания.

Глава 18. Имитационное моделирование

Интервал времени	Времена ожидания
0-100	10, 20,13, 14, 8,15, 6,8
100-200	12, 30, 10, 14, 16
200 - 300	15, 17, 20, 22
300 - 400	10, 20, 30, 15, 25, 31
400 - 500	15, 17, 20, 14, 13
500 - 600	25, 30, 15

3. Пусть в условиях примера 18.6.2 начальные точки циклов совпадают с теми моментами времени, когда все три обслуживающих устройства становятся не­занятыми. На рис. 18.13 эти точки соответствуют моментам времени t = 10, 17, 24 и 33. Определите 95%-ный доверительный интервал для занятости обслужи­вающих устройств, основываясь на новом определении точек начала циклов.

4. Для сервисной системы с одним обслуживающим устройством проводится имитация ее работы на протяжении 100 часов. Результаты имитации пока­зывают, что обслуживающее устройство было занято на протяжении таких интервалов времени: (0, 10), (15, 20), (25, 30), (35, 60), (70, 80) и (90, 95). Ос­тальное время из интервала имитации обслуживающее устройство было сво­бодно. Длина переходного периода равна 10 часов.

a) Определите начальные точки, необходимые для применения метода циклов.

b) Методом циклов определите 95%-ный доверительный интервал для вре­мени занятости обслуживающего устройства.

c) С помощью метода подынтервалов решите ту же задачу при числе интер­валов п = 5. Определите соответствующий 95%-ный доверительный ин­тервал и сравните его с результатом, полученным методом циклов.

18.7. ЯЗЫКИ ИМИТАЦИОННОГО МОДЕЛИРОВАНИЯ

Реализация имитационных моделей связана с двумя различными типами вы­числений: 1) манипуляции регистрацией, которые имеют дело с хронологическим накоплением и обработкой событий модели, и 2) вычисления, связанные с генери­рованием случайных чисел и сбором статистических данных, относящихся к моде­ли. Вычисления первого типа основываются на различных логических методах об­работки списков, а вычисления второго типа обычно очень громоздки и занимают много времени. Природа этих вычислений делает компьютер важным инструмен­том в реализации имитационных моделей и, в свою очередь, стимулирует создание специализированных языков программирования, что позволяет выполнять эти вы­числения более удобным и эффективным способом.

Доступные языки дискретного имитационного моделирования делятся на две большие категории.

1. Языки, ориентированные на планирование событий.

2. Языки, ориентированные на обработку процессов (процедур).

При использовании языков, ориентированных на планирование событий, пользо­вателю необходимо указать действия, связанные с каждым событием, происхо­дящим в системе, аналогично тому, как они были представлены в разделе 18.5.1.

18.7. Языки имитационного моделирования

Основная роль программы в этом случае сводится к автоматизации процесса получе­ния случайных значений, имеющих соответствующее распределение, хронологиче­скому накоплению, обработке событий и сбору данных, относящихся к модели.

Процедурно-ориентированные языки используют блоки (или узлы), которые можно соединять для формирования сети, которая описывает движение транзак­ций или объектов (т.е. клиентов) в системе. Например, наиболее известными типа­ми узлов в любом языке имитационного моделирования являются источник, в ко­тором транзакции создаются, очередь, где при необходимости они могут ожидать, и сервисы, где выполняется обслуживание. Каждый из этих узлов при его опреде­лении обеспечивается всей необходимой информацией, позволяющей выполнять имитацию автоматически. Например, если время между поступлениями заказов для источника определено, процедурно-ориентированный язык автоматически "знает", когда могут возникнуть события, связанные с прибытием заказа. В дейст­вительности каждый узел имеет установленные инструкции, т.е. точно определяет как и когда транзакции перемещаются по имитационной сети.

Процедурно-ориентированные языки управляются теми же действиями, что и язы­ки, ориентированные на планирование событий. Отличие состоит в том, что эти дейст­вия автоматизированы для освобождения пользователя от утомительных вычисли­тельных и логических деталей. В некотором отношении можно рассматривать процедурно-ориентированные языки как основанные на концепции "черного ящика", имеющего заданные "вход" и "выход". Это означает, что процедурно-ориентированные языки просты и легки в использовании благодаря гибкости процесса моделирования.

Наиболее известными языками программирования, ориентированными на пла­нирование событий, являются SIMSCRIPT, SLAM и SIMAN. Развитие этих языков на протяжении многих лет привело к тому, что они включают и возможности процедур­но-ориентированных языков. Все эти языки позволяют пользователю создавать мо­дели (или их отдельные части) на языках высокого уровня, таких как FORTRAN и С. Это необходимо для того, чтобы дать возможность пользователю программировать сложные логические операции, которые невозможно или трудно осуществить обыч­ными средствами этих языков. Главной причиной этого является ограничительная и, возможно, запутанная процедура, с помощью которой данные языки перемещают транзакции (или объекты) между очередью и сервисами, присутствующими в модели.

Первым процедурно-ориентированным языком был GPSS. Этот язык, первая версия которого появилась в начале 1960-х годов, совершенствовался на протяже­нии нескольких лет, чтобы удовлетворить новым требованиям, связанным с моде­лированием сложных систем. Чтобы эффективно использовать этот язык, пользо­вателю необходимо настроить примерно восемьдесят различных блоков. Несмотря на многие годы использования GPSS, язык все еще имеет некоторые трудно объяс­нимые особенности моделирования. Примером может служить необходимость ап­проксимировать непрерывные распределения вероятностей их кусочно-линейными аналогами. Справедливости ради заметим, что некоторые последние версии этого языка обеспечивают возможности использования и непрерывных распределений (например, экспоненциального и нормального). Однако при имеющихся громад­ных возможностях современных компьютеров трудно понять, почему такое пре­пятствие продолжает так долго существовать.

В настоящее время на рынке программных продуктов для моделирования доми­нируют коммерческие пакеты, такие как Arena, AweSim и GPSS/H. Эти пакеты об­ладают развитым интерфейсом, что упрощает пользователю процесс создания ими­тационных моделей. Они также имеют анимационные средства, визуализирующие изменения, происходящие в модели во время имитации. Однако для опытных поль­

Глава 18. Имитационное моделирование

зователей такие "дружественные" интерфейсы могут значительно замедлить процесс создания имитационных моделей. Поэтому нет ничего удивительного в том, что мно­гие разработчики имитационных моделей предпочитают использовать в своей работе языки программирования "общего назначения", такие как С, Basic или FORTRAN.

УПРАЖНЕНИЯ 18.7⁷

1. Клиенты случайным образом прибывают на почтовое отделение, в котором работают три служащих. Время между их приходами является случайной величиной, распределенной по экспоненциальному закону с математическим ожиданием 5 мин. Время, затрачиваемое служащим на обслуживание кли­ента, имеет экспоненциальное распределение с математическим ожиданием 10 мин. Все прибывающие клиенты формируют единую очередь и ожидают первого освободившегося служащего. Используйте имитационную модель сис­темы для исследования ее работы на протяжении 480 мин., чтобы определить

a) среднее число клиентов, ожидающих в очереди;

b) среднюю занятость служащих.

2. Телевизионные блоки прибывают для проверки на ленточный конвейер с по­стоянной скоростью пять единиц в час. Время проверки блока является слу­чайной величиной, равномерно распределенной между 10 и 15 мин. Преды­дущий опыт показывает, что 20 % проверенных блоков должны быть отрегулированы и отправлены на повторную проверку. Время регулировки также является случайной величиной, равномерно распределенной между 6 и 8 мин. Используйте имитационную модель системы для исследования ее работы на протяжении 480 мин., чтобы вычислить

a) среднее время, необходимое для проверки одного блока;

b) среднее количество повторных проверок, которые должен пройти телеви­зионный блок перед выходом из системы.

3. Мышь находится в лабиринте и отчаянно пытается из него выбраться. Про­ведя в попытках выбраться от 1 до 3 мин. с равномерным распределением, в 30 % случаев она находит выход из лабиринта. В случае неудачи она бродит бесцельно от 2 до 3 мин. с равномерным распределением и, в конце концов, останавливается в месте, откуда она начинала, но лишь для того, чтобы по­пробовать еще раз. Мышь может пытаться выбраться на свободу столько раз, сколько она хочет, но всему есть предел. Истратив много энергии на много­численные попытки выбраться на свободу, мышь непременно умрет, если не ус­пеет выбраться за период времени, имеющий нормальное распределение с мате­матическим ожиданием 10 мин. и стандартным отклонением 2 мин. Постройте имитационную модель для оценки вероятности того, что мышь освободится. С этой целью предположите, что в модели будет использовано 100 мышей.

4. На финальной стадии сборки автомобиль движется по конвейеру между двумя параллельными рабочими местами, чтобы можно было выполнять работы как с левой, так и с правой стороны одновременно. Время выполнения работ с каждой стороны является равномерно распределенной случайной величиной с интервалом изменения от 15 до 20 мин. и от 18 до 22 мин. соответственно.

⁷ Решите эти упражнения, используя какой-либо язык имитационного моделирования по своему выбору или языки программирования Basic, FORTRAN или С.

Литература

Конвейер прибывает на рабочие места каждые 20 минут. Постройте имитаци­онную модель работы сборочного конвейера на протяжении 480 мин. для опре­деления времени использования рабочих мест слева и справа от машины.

5. Время между прибытием машин на пункт мойки с одним обслуживающим устройством является случайной величиной, распределенной по экспоненци­альному закону с математическим ожиданием 10 мин. Автомобили выстраи­ваются в одну очередь, которая может поместить максимум пять ожидаю­щих автомобилей. Если очередь заполнена, вновь прибывший автомобиль уезжает. Время мойки машины является случайной величиной, равномерно распределенной на интервале от 10 до 15 мин. Постройте имитационную мо­дель работы системы на протяжении 960 мин. и найдите время пребывания автомобиля на пункте мойки.

ЛИТЕРАТУРА

1. Box G. and Muller М. "A Note on the Generation of Random Normal Deviates", An­nals of Mathematical Statistics, Vol. 29, pp.610-611, 1958.

2. Law A. and Kelton W. Simulation Modeling & Analysis, 3rd ed., McGraw-Hill, New York, 2000.

3. Ross S. A Course of Simulation, Macmillan, New York, 1990.

4. Rubenstein R., Melamed B. and Shapiro A. Modern Simulation and Modeling, Wiley, New York, 1998.

5. Taha A. Simulation Modeling and SIMNET, Prentice Hall, Upper Saddle River, N. J., 1988.

Литература, добавленная при переводе

1. Ермаков С. М. Метод Монте-Карло и смежные вопросы. — М.: Наука, 1975.

2. Мур Дж., Уэдерфорд Л. Экономическое моделирование в Microsoft Excel. — М.: Издательский дом "Вильяме", 2004.

3. Нейлор Т. Машинные имитационные эксперименты с моделями экономиче­ских систем. — М.: Мир, 1978.

4. Соболь И. М. Численные методы Монте-Карло. — М.: Наука, 1973.

5. Шеннон Р. Имитационное моделирование систем — искусство и наука. — М.: Мир, 1978.

ГЛАВА 19

МАРКОВСКИЕ ПРОЦЕССЫ ПРИНЯТИЯ РЕШЕНИЙ

В этой главе рассмотрено применение методов динамического программирова­ния для решения стохастических задач, где процесс принятия решений можно представить конечным числом состояний. Переходные вероятности между состоя­ниями описывают марковскую цепь¹. Структура вознаграждений в подобном про­цессе представима в виде матрицы, элементами которой являются величины дохо­да (или затраты), возникающие при переходе из одного состояния в другое. Матрица переходных вероятностей и матрица доходов зависят от альтернатив ре­шения, которыми располагает лицо, принимающее решение. Целью задачи явля­ется формирование оптимальной стратегии, максимизирующей ожидаемый доход от процесса, имеющего конечное или бесконечное число этапов.

19.1. МАРКОВСКАЯ ЗАДАЧА ПРИНЯТИЯ РЕШЕНИЙ

Мы используем простой пример, который будет служить нам на протяжении всей главы. Несмотря на простоту, парафраз этого примера находит применение во многих приложениях в области управления запасами, замены оборудования, кон­троля и регулирования денежных потоков и др.

Каждый год в начале сезона садовник проводит химический анализ состояния почвы в своем саду. В зависимости от результатов анализа продуктивность сада на новый сезон оценивается как 1) хорошая, 2) удовлетворительная или 3) плохая.

В результате многолетних наблюдений садовник заметил, что продуктивность в текущем году зависит только от состояния почвы в предыдущем году. Поэтому ве­роятности перехода почвы из одного состояния продуктивности в другое для каж­дого года можно представить как вероятности перехода в следующей цепи Маркова.

Состояние системы в следующем году

Состояние системы в текущем году

1 2 3

f0,2 0,5 0,3) 0 0,5 0,5 0 0 1

Р¹

¹ Обзор теории цепей Маркова приведен в разделе 19.5.

Глава 19. Марковские процессы принятия решений

Переходные вероятности в матрице Р' показывают, что продуктивность почвы в текущем году не лучше, чем в предыдущем. Например, если состояние почвы в текущем году удовлетворительное (состояние 2), то в следующем году оно может остаться удовлетворительным с вероятностью 0,5 или стать плохим (состояние 3) с той же вероятностью.

В результате различных агротехнических мероприятий садовник может изме­нить переходные вероятности Р¹. Обычно для повышения продуктивности почвы применяются удобрения. Эти мероприятия приводят к новой матрице переходных вероятностей Р².

1 2 ⁽ 0,3 0,6 0,1 0,6 ^0,05 0,4

0,1 ⁴ 0,3 0,55,

Чтобы рассмотреть задачу принятия решений в перспективе, садовник связыва­ет с переходом из одного состояния почвы в другое функцию дохода (или структуру вознаграждения), которая определяет прибыль или убыток за одногодичный пери­од в зависимости от состояний, между которыми осуществляется переход. Так как садовник может принять решение использовать или не использовать удобрения, его доход или убыток будет изменяться в зависимости от принятого решения. Мат­рицы R¹ и R² определяют функции дохода (в сотнях долл.) и соответствуют матри­цам переходных вероятностей Р¹ и Р².

3^

-1

'6

7 6

Элементы rfj матрицы R² учитывают затраты, связанные с применением удобрения.

Например, если система находится в состоянии 1 и остается в этом состоянии и в сле­дующем году, то доход составит г,² = 6, если же удобрения не используются, = 7.

Какая же задача принятия решений стоит перед садовником? Сначала необхо­димо установить, будет ли деятельность садовника продолжаться ограниченное число лет или бесконечно. В соответствии с этим рассматриваются задачи принятия решения с конечным и бесконечным числом этапов. В обоих случаях, имея результа­ты химического анализа почвы (состояние системы), садовник должен выбрать наи­лучшую стратегию поведения (удобрять или не удобрять почву). При этом оптималь­ность принятого решения основывается на максимизации ожидаемого дохода.

Садовника может также интересовать оценка ожидаемого дохода по заранее оп­ределенной стратегии поведения при том или ином состоянии системы. Например, он может принять решение всегда применять удобрения, если состояние почвы плохое (состояние 3). В таком случае говорят, что процесс принятия решений опи­сывается стационарной стратегией.

19.2. Модель динамического программирования с конечным числом этапов

Каждой стационарной стратегии соответствуют свои матрицы переходных веро­ятностей и доходов, которые можно построить на основе матриц Р¹, Р², R¹ и R². На­пример, для стационарной стратегии, требующей применения удобрения только тогда, когда состояние почвы плохое (состояние 3), результирующие матрицы пе­реходных вероятностей и доходов задаются следующими выражениями.

	'0,2	0,5	0,3 '		'1 6 Зч
р =		0,5	0,5	, R =	0 5 1
	,0,05	0,4	0,55,		ч6 3 -2,

Эти матрицы отличаются от Р¹ и R¹ только третьей строкой, включенной в них из матриц Р² и R². Причина этого в том, что Р² и R² — матрицы, соответствующие ситуации, когда удобрения применяются при любом состоянии почвы.

УПРАЖНЕНИЯ 19.1

1. В задаче садовника определите матрицы Р и R, соответствующие стационар­ной стратегии, требующей использования удобрений при удовлетворитель­ном и плохом состояниях почвы.

2. Определите все стационарные стратегии в примере с садовником.

19.2. МОДЕЛЬ ДИНАМИЧЕСКОГО ПРОГРАММИРОВАНИЯ С КОНЕЧНЫМ ЧИСЛОМ ЭТАПОВ

Предположим, что садовник планирует прекратить занятие садоводством через N лет. В этом случае необходимо определить стратегию поведения (удобрять или не удоб­рять почву) для каждого года планирования. Очевидно, что оптимальной стратегией будет такая, при которой садовник получит наибольший ожидаемый доход через N лет.

Пусть k = 1 или 2 обозначает две возможные (альтернативные) стратегии пове­дения садовника. Матрицы Р^к и R^k, представляющие переходные вероятности и функцию дохода для альтернативы k, определены в разделе 19.1; здесь они при­водятся для удобства.

	'0,2	0,5	0,3'		'1	6 зч
		0,5	0,5	• R'=NII=		5 1
	ч 0		1 ,		,0	0 -1,
	' 0,3	0,6	о,П		'6	5 -Г
*2=И1=	0,1	0,6	0,3	. R2=lk2ll=		4 0
	,0,05	0,4	0,55,		,6	3 -2,

Задачу садовника можно представить как задачу динамического программиро­вания (ДП) с конечным числом этапов следующим образом. Пусть число состояний для каждого этапа (года) равно т (3 в примере с садовником). Обозначим через f_n(i) оптимальный ожидаемый доход, полученный на этапах от п до N включительно при условии, что система находится в начале этапа п в состоянии L

Обратное рекуррентное уравнение, связывающее f_n и f_n+1, можно записать в виде

Л(0 = ™*{?>* [tf+/.♦. 0')]}. » = 1.2, ...,АГ,

где f_N+l(J) = 0 для всех j.

Глава 19. Марковские процессы принятия решений

Приведенное уравнение основано на том, что накапливающийся доход ^rl + fn*iU) получается в результате перехода из состояния I на этапе п в состояние /

на этапе п + 1 с вероятностью /»*. Введя обозначение

рекуррентное уравнение ДП можно записать следующим образом:

A(/) = max{vf},

/„(/) = max|vf+Xp*/„_+l(y)J, « = 1,2, ...,N-l.

Проиллюстрируем использование рекуррентного уравнения для вычисления ве­личин v* в задаче садовника для ситуации, когда удобрения не применяются (k = 1).

у,¹ =0,2x7 + 0,5x6 + 0,3x3 = 5,3,

v =0x0 + 0,5x5 + 0,5x1 = 3,

Ц=0х0 + 0х0 + 1х(-1) = -1.

Эти значения показывают, что если состояние почвы в начале года оказывается хо­рошим (состояние 1), то при одном переходе ожидаемый годовой доход составляет 5,3. Аналогично, если состояние почвы удовлетворительное, ожидаемый годовой доход составит 3, а в случае плохого будет равен -1.

Пример 19.2.1

В этом примере задача садовника решается при данных, заданных матрицами Р¹, Р², R¹ и R². Предполагается, что горизонт планирования включает 3 года (N= 3).

Так как значения v* многократно используются в вычислениях, для удобства они

сведены в таблицу. Напомним, что значение к = 1 соответствует решению "не удоб­рять", к = 2 — "удобрять".

/				2 V,
		5,3		4,7
				3,1
		-1		0,4
ЭтапЗ
				Оптимальное решение
/'	к= 1	к = 2	ад	к"
	5,3	4,7	5,3
		3,1	3,1
	-1	0,4	0,4

19.2. Модель динамического программирования с конечным числом этапов 741

Этап^

	Ч+л/з(1) + Л*/з(2) + л'/з(3)				Оптимальное решение
/	к = 1		к = 2		Hi) к
	5,3 + 0,2 х 5,3 + 0,5 х 3,1 + 0,3 х 0,4 =	= 8,03	4,7 + 0,3 х 5,3 + 0,6 х 3,1 + 0,1 х 0,4	= 8,19	8,19 2
	3 + 0 х 5,3 + 0,5 х 3,1 + 0,5 х 0,4 =	4,75	3,1 + 0,1 х 5,3 + 0,6 х 3,1 + 0,3 х 0,4	= 5,61	5,61 2
	-1 + 0 х 5,3 + 0 х 3,1 + 1 х 0,4 = -0,6	0,4 + 0,05 х 5,3 + 0,4 х 3,1 + 0,55 х 0,4	= 2,13	2,13 2
Этап 1
	*-+Р»Ш + Р-гШ + Р«Ш				Оптимальное решение
/	к= 1		к = 2		Щ *
	5,3 + 0,2 х 8,19 + 0,5 х 5,61 + 0,3 х 2,13 =	= 10,38 4,7 + 0,3 x 8,19 + 0,6 x 5,61 +0,1 х2,13 =	10,74	10,74 2
	3 + 0 х 8,19 + 0,5 х 5,61 + 0,5 х 2,13 =	6,87	3,1 + 0,1 х 8,19 + 0,6 х 5,61 + 0,3 х 2,13	= 7,92	7,92 2
	-1 + 0 х 8,19 + 0 х 5,61 + 1 х 2,13 =	1,13	0,4 + 0,05 х 8,19 + 0,4 х 5,61 + 0,55 х 2,13 = = 4,23	4,23 2

Оптимальное решение показывает, что в 1-й и 2-й годы садовник должен применять удобрения (к' = 2) независимо от состояния системы (состояния почвы по данным хи­мического анализа). На 3-й год садовнику следует применять удобрения только то­гда, когда система находится в состояниях 2 или 3 (т.е. при удовлетворительном или плохом состоянии почвы). Суммарный ожидаемый доход за три года составитyj(l) = 10,74 при хорошем состоянии системы в 1-й год,/,(2) = 7,92 — при удовлетворитель­ном состоянии системы в 1-й год и/ДЗ) = 4,23 — при плохом состоянии.

Задача при конечном горизонте планирования (решенная выше задача садовни­ка) может быть обобщена в двух направлениях. Во-первых, переходные вероятно­сти и функции дохода не обязательно должны быть одинаковы для каждого года. Во-вторых, можно использовать коэффициент переоценки (дисконтирования) ожи­даемых доходов для последовательных этапов, вследствие чего значения /,(/) будут представлять собой приведенные величины ожидаемых доходов по всем этапам.

В первом случае значения доходов и переходные вероятности р* должны

быть функциями этапа п. Здесь рекуррентное уравнение динамического програм­мирования принимает вид

/_A.(.-) = max{vf-"},

/Л|>шах|^+£/»;••/„,(;)}. "=U, ...,N-1

где

н

Второе обобщение заключается в следующем. Пусть а(< 1) — годовой коэффи­циент переоценки (дисконтирования), тогда D долларов будущего года равны aD долларам настоящего года. При введении коэффициента переоценки исходное ре­куррентное уравнение преобразуется в следующее:

Глава 19. Марковские процессы принятия решений

/„(/) = max {vf},

/„(,) = maxjvf + af>*/„_+l(y)J, « = 1,2, ...,N-l.

УПРАЖНЕНИЯ 19.2

1. Фирма ежегодно оценивает положение со сбытом одного из видов своей ос­новной продукции и дает ему удовлетворительную (состояние 1) или не­удовлетворительную оценку (состояние 2). Необходимо принять решение о целесообразности рекламирования этой продукции в целях расширения ее сбыта. Приведенные ниже матрицы Р¹ и Р² определяют переходные ве­роятности при наличии рекламы и без нее в течение любого года. Соответ­ствующие доходы заданы матрицами R¹ и R². Найдите оптимальные реше­ния для последующих трех лет.

'0,9

Р' =

10,6

'0,7 0,2

0, 0,4

0,3 0,8

R' =

-1 -3

-1

Компания может провести рекламную акцию с помощью одного из трех средств массовой информации: радио, телевидения или газеты. Недельные затраты на рекламу с помощью этих средств оцениваются в 200, 900 и 300 долл. соответственно. Компания оценивает недельный объем сбыта своей продук­ции по трехбалльной шкале как удовлетворительный (1), хороший (2) и от­личный (3). Ниже указаны переходные вероятности, соответствующие каж­дому из трех средств массовой информации.

'0,4 0,1 1,0,1

Радио 2 3 0,5 0,0 0,7 0,2 0,2 0,7

Телевидение 1 2 3 0,2 0,6 0,7

'0,7 0,3 ,0,1

0,0 0,1 0,2

(0,2 0 0

Газета 2 3 0,5 0,7 0,2

0,3 0,3 0,8

Соответствующие недельные доходы (в тыс. долл.) равны следующему.

Радио '400 520 600"! 300 400 700 200 250 500,

Телевидение '1000 1300 1600^ 800 1000 1700 600 700 1100

Газета Г 400 530 710"! 350 450 800 250 400 650

Найдите оптимальную стратегию рекламы для последующих трех недель.

3. Задача управления запасами. Магазин электротоваров в целях быстрого удовлетворения спроса покупателей на холодильники может размещать за­казы в начале каждого месяца. Каждое размещение заказа приводит к по­стоянным затратам в 100 долл. Затраты на хранение одного холодильника в течение месяца равны 5 долл. Потери магазина при отсутствии холодиль­ников оцениваются в 150 долл. за каждый холодильник в месяц. Месячный спрос на холодильники задается следующим распределением вероятностей.

19.3. Модель с бесконечным числом этапов

Спрос х
рМ	0,2	0,5	0,3

Магазин реализует следующую стратегию: максимальный уровень запаса не должен превышать двух холодильников в течение любого месяца.

a) Определите переходные вероятности при различных альтернативах реше­ния этой задачи.

b) Определите ожидаемые месячные затраты на хранение запаса как функ­цию состояния системы и альтернативных решений.

c) Определите оптимальную стратегию размещения заказов на последующие 3 месяца.

4. Выполните задания предыдущего упражнения, предполагая, что плотности вероятностей спроса на следующий квартал определяются значениями из следующей таблицы.

		Месяц
Спрос, х
	0,1	0,3	0,2
	0,4	0,5	0,4
	0,5	0,2	0,4

19.3. МОДЕЛЬ С БЕСКОНЕЧНЫМ ЧИСЛОМ ЭТАПОВ

Существует два метода решения задачи с бесконечным числом этапов. Первый метод основан на переборе всех возможных стационарных стратегий в задаче при­нятия решений. Этот подход, по существу, эквивалентен методу полного перебора, и его можно использовать только тогда, когда общее число стационарных страте­гий с точки зрения практических вычислений достаточно мало. Второй метод, на­зываемый методом итераций по стратегиям, как правило, более эффективен, так как определяет оптимальную стратегию итерационным путем.

19.3.1. Метод полного перебора

Предположим, что в задаче принятия решений имеется S стационарных страте­гий. Пусть Р'иК' — матрицы переходных (одношаговых) вероятностей и доходов, соответствующие применяемой стратегии, 8 = 1,2, S. Метод перебора включает следующие действия.

Шаг 1. Вычисляем v,' — ожидаемый доход, получаемый за один этап при стратегии s для заданного состояния I, i = 1, 2.....т.

Шаг 2. Вычисляем п' — долгосрочные стационарные вероятности мат­рицы переходных вероятностей Р', соответствующие стратегии s. Эти вероятности (если они существуют) находятся из уравнений

Глава 19. Марковские процессы принятия решений

где я*=(я;,я'₂,...Х).

Шаг 3. Вычисляем по следующей формуле Е' ожидаемый доход за один шаг (этап) при выбранной стратегии s.

т

i-i

Шаг 4. Оптимальная стратегия s* определяется из условия, что

Е' =тах{Е'}.

Проиллюстрируем этот метод на примере задачи садовника при бесконечном го­ризонте планирования.

Пример 19.3.1

В задаче садовника имеется восемь стационарных стратегий, представленных в следующей таблице.

Стационарная стратегия, s	Действия
	Не применять удобрения вообще
	Применять удобрения независимо от состояния почвы
	Применять удобрения, если почва находится в состоянии 1
	Применять удобрения, если почва находится в состоянии 2
	Применять удобрения, если почва находится в состоянии 3
	Применять удобрения, если почве находится в состоянии 1 или 2
	Применять удобрения, если почва находится в состоянии 1 или 3
	Применять удобрения, если почва находится в состоянии 2 или 3

Матрицы Р⁵ и R¹ для стратегий от 3 до 8 получаются из аналогичных матриц для стратегий 1 и 2. Таким образом, имеем

	'0,2	0,5 0,3Ч			'1		У
р =		0,5 0,5		R =
	,о	0 1 ,			,o		-к
	'0,3	0,6 0,1 ^			'6		-Г
Р2 =	0,1	0,6 0,3	, R2
	,0,05	0,4 0,55,			,6	3 •	-2,
	'0,3	0,6 0,Г			'6		-Г
Р3 =		0,5 0,5		R3 =				»
	,о				,0		-lj
	'0,2	0,5 0,3N			'7		зч
Р4 =	0,1	0,6 0,3		R4 =
		0 1 ,					-к

19.3. Модель с бесконечным числом этапов

	'0,2	0,5	0,3 4		'1		3N
Р5 =		0,5	0,5	, R5 =
	0,05	0,4	0,55,		,6
	'0,3	0,6	0,Г			'6		-Г
Р6 =	0,1	0,6	0,3		R6 =
	,о							Ч
	'0,3	0,6	о,П		'6		-Г
Р7 =		0,5	0,5	, R7 =
	,0,05	0,4	0,55,		,6		-2,
	г 0,2	0,5	0,3'		'1		3'
Р8 =	0,1	0,6	0,3	, R8 =
	^0,05	0,4	0,55,		,6		"2,

Результаты вычислений значений v* приведены в следующей таблице.

 

S		v;
/= 1	/= 2	/= 3
	5,3	3,0	-1,0
	4,7	3,1	0,4
	4,7	3,0	-1,0
	5,3	3,1	-1,0
	5,3	3,0	0,4
	4,7	3,1	-1,0
	4,7	3,0	0,4
	5,3	3,1	0,4

Стационарные вероятности находятся из уравнений

я*Р*=я

л, + л₂+...+ л„, =1.

Для иллюстрации применения этих уравнений рассмотрим стратегию s = 2. Соот­ветствующие уравнения имеют следующий вид.

0,3л, + 0,1л₂ + 0,05л₃ =тс,, 0,6л, + 0,6л₂ + 0,4л₃ = л₂, 0,1л, + 0,3л₂ +0,55л₃ = л₃, л, + л₂ + л₃ = 1.

(Отметим, что одно из первых трех уравнений избыточно.) Решением системы будет

₂__6_ ₂_31_ ₂_22 ~ 59' "² ~59' *' ~ 59'

Глава 19. Марковские процессы принятия решений

В данном случае ожидаемый годовой доход равен

Е¹ = ]Гя? v,² = — (6 х 4,7 + 31 х 0,31 + 22 х 0,4) = 2,256.

;=| 59

Результаты вычислений и для всех стационарных стратегий приведены в сле­дующей таблице. (Отметим, что хотя каждая из стратегий 1, 3, 4 и 6 имеет погло­щающее состояние (состояние 3), это никоим образом не влияет на результаты вы­числений. По этой причине л_х = л_г = 0тл л_ъ = 1 для всех этих стратегий.)

S	К	А	<
				-1,0
	6/59	31/59	22/59	2,256
				0,4
				-1,0
	5/154	69/154	80/154	1,724
				-1,0
	5/137	62/137	70/137	1,734
	12/135	69/135	54/135	2,216

Из этой таблицы видно, что стратегия 2 дает наибольший ожидаемый годовой до­ход. Следовательно, оптимальная долгосрочная стратегия требует применения удобрений независимо от состояния системы.

УПРАЖНЕНИЯ 19.3.1

1. Решите задачу из упражнения 19.2.1 методом полного перебора при беско­нечном числе этапов.

2. Решите задачу из упражнения 19.2.2 при бесконечном горизонте планирова­ния методом полного перебора.

3. Решите задачу из упражнения 19.2.3 методом полного перебора, предпола­гая, что горизонт планирования бесконечен.

19.3.2. Метод итераций по стратегиям без дисконтирования

Чтобы оценить трудности, связанные с применением метода полного перебора, предположим, что у садовника вместо двух имеется четыре стратегии поведения (альтернативы): не удобрять, удобрять один раз в сезон, удобрять дважды и удоб­рять трижды в сезон. В этом случае общее число стратегий, имеющихся в распоря­жении садовника, составляет 4* = 256 стационарных стратегий. Таким образом, при увеличении числа альтернатив с 2 до 4 число стационарных стратегий возрас­тает по экспоненте с 8 до 256. Трудно не только перечислить в явном виде все эти стратегии, но и может оказаться также недопустимо большим объем вычислений, требуемых для оценки всего множества стратегий.

19.3. Модель с бесконечным числом этапов

Метод итераций по стратегиям основывается на следующем. Как показано в разделе 19.2, для любой конкретной стратегии ожидаемый суммарный доход за л-й этап определяется рекуррентным уравнением

т

/.(0 = ^v<+Z/V/:*. (Л ' = 1.2,..., т.

Это уравнение и служит основой метода итераций по стратегиям. Однако, чтобы сделать возможным изучение асимптотического поведения процесса, вид уравне­ния нужно немного изменить. В отличие от величины п, которая фигурирует в уравнении и соответствует ге-му этапу, обозначим через rj число оставшихся для анализа этапов. Тогда рекуррентное уравнение записывается в виде

т

/,(0 = v₍ + I^/,-,(у). ' = 1.2,..., т.

Здесь — суммарный ожидаемый доход при условии, что остались не рассмотрен­ными п этапов. При таком определении п можно изучить асимптотическое поведе­ние процесса, полагая при этом, что л -» оо.

Обозначим через я = (я,,п₂,...,п_и) вектор установившихся вероятностей состоя­ний с матрицей переходных вероятностей Р=|ру| и пусть £ = n,v, + t₂v₂+... + 7c_mv„ —

ожидаемый доход за этап, вычисленный по схеме раздела 19.3.1, тогда можно по­казать, что при достаточно большом п

/„(') = л*+ /(').

где f(i) — постоянный член, описывающий асимптотическое поведение функции f,j(i) при заданном состоянии i.

Так как /%(/) представляет суммарный оптимальный доход за п этапов при за­данном состоянии i,