Имя Узел Поток Спрос От В Единичный поток

N1 | К

N2 Я

N3 Т а

N4 1 4

N5 Т Si -60

о о о

1 1 1 1

2 2 2 2 3

3 2 3 _й

3 5

4 1 4 2

2 _1

³! ¹

4 1

3 4 5 1

Поиск решении

Установить целевую ячейку: Равной: <? максимальному значению

^г м^имальному значению Иэменая ячей*

Значению: RT

Выполнить ) Закрыть

ftB$20-$8$39 Ограничения:

$8$20,$В$39 <= $С$20:$С$Э9 tF$20:tFt22 = $GJ20:$G$22

Предположить |

Добавить | Изменить {

Параметры |

1!лалить

J

Восданоеить | Справка

Рис. 6.35. Определение максимального потока в Excel

Решение N1-N2 = 20, Nl-N3 = 30, N1-N4 = 10, N2-N5 = 20, N3-N4=10, N3-N5 = 20 и N4-N5 = 20, показанное на рис. 6.35, дает максимальный поток, равный 60 единицам.

6.5. Задача нахождения потока наименьшей стоимости

УПРАЖНЕНИЯ 6.4.4

1. Решите задачу из упражнения 6.4.2.2 с помощью средства Поиск решения.

2. Решите задачу из упражнения 6.4.2.5 с помощью средства Поиск решения.

Задача нахождения потока наименьшей стоимости в сети с ограниченной пропу­скной способностью обобщает задачу определения максимального потока по сле­дующим направлениям.

1. Каждой дуге поставлена в соответствие (неотрицательная) стоимость прохо­ждения единицы потока по данной дуге.

2. Дуги могут иметь положительную нижнюю границу пропускной способности.

3. Любой узел сети может выступать в качестве как источника, так и стока.

В рассматриваемой задаче необходимо найти потоки по дугам, минимизирую­щие общую стоимость прохождения потока по сети; при этом должны удовлетво­ряться ограничения на пропускные способности дуг и на величины предложений и спроса отдельных (или всех) узлов. Сначала опишем сетевую модель с заданными стоимостями прохождения потока по дугам и сформулируем соответствующую за­дачу линейного программирования. Эта задача далее будет использована как осно­ва для построения специального симплексного алгоритма, предназначенного для решения данной сетевой задачи.

6.5.1. Сетевая модель

Рассмотрим сеть G = (N, А) с ограниченной пропускной способностью, где N — множество узлов, А — множество дуг. Обозначим

x_tj — величина потока, протекающего от узла i к узлу у,

ц,. (?,.) — верхняя (нижняя) граница пропускной способности дуги (i, j),

c_tj — стоимость прохождения единицы потока по дуге (t, j),

f. — величина "чистого" результирующего потока, протекающего через узел i.

На рис. 6.36 показано, как на схемах сетей будем отображать определенные па­раметры дуг. Метка [/,] указывает положительное (отрицательное) значение пред­ложения (спроса), соответствующего узлу i.

6.5. ЗАДАЧА НАХОЖДЕНИЯ ПОТОКА НАИМЕНЬШЕЙ СТОИМОСТИ

Рис. 6.36. Обозначение параметров дуг

Глава 6. Сетевые модели

Пример 6.5.1

Компания GrainCo снабжает зерном из трех зернохранилищ три птицеводческие фермы. Предложение зернохранилищ составляет 100, 200 и 50 тысяч бушель зер­на, а спрос ферм — 150, 80 и 120 тысяч бушель соответственно. Компания может транспортировать зерно по железной дороге, за исключением трех маршрутов, где используется автомобильный транспорт.

На рис. 6.37 показаны возможные маршруты между зернохранилищами и птице­водческими фермами. Зернохранилища представлены узлами 1, 2 и 3; их предло­жения указаны метками [100], [200] и [50] соответственно. Фермы обозначены уз­лами 4, 5 и 6 с величинами спроса [-150], [-80] и [-120]. Маршруты транспортировки зерна показаны на рис. 6.37 дугами, соединяющими узлы сети. Дуги (1, 4), (3, 4) и (4, 6) соответствуют автомобильным маршрутам. Эти маршруты имеют верхние и нижние границы пропускных способностей. Например, по мар­шруту (1, 4) можно провести от 50 до 80 тысяч бушелей зерна. Другие маршруты соответствуют железнодорожному транспорту, пропускная способность которого практически не ограничена. Стоимость транспортировки одного бушеля зерна по­казана возле каждой дуги.

[-150]

[-80]

Рис. 6.37. Схема сети для примера 6.5.1

УПРАЖНЕНИЯ 6.5.1 -

1. Компания разрабатывает 4-этапный план производства некоего продукта со­гласно следующим данным.

Этап	Объем спроса	Стоимость единицы продукции (долл.)	Стоимость хранения единицы продукции (долл.)

Сформулируйте данную задачу как сетевую модель, предполагая, что заказы нельзя выполнять "задним числом".

6.5. Задача нахождения потока наименьшей стоимости

2. Пусть в предыдущем упражнении возможна недопоставка продукции со штрафом 1,50 долл. за единицу продукции при задержке в течение одного этапа. Сформулируйте задачу как сетевую модель.

3. Пусть в упражнении 1 производственные возможности каждого из четырех этапов составляют соответственно 110, 95, 125 и 100 единиц продукции, что не позволяет выполнить все заказы (без недопоставок продукции) в срок. Штраф за недопоставку единицы продукции равен 1,50 долл. при задержке в течение одного этапа. Сформулируйте задачу как сетевую модель.

4. Химическая компания владеет двумя заводами, которые производят опреде­ленные химические компоненты для двух клиентов; потребности этих кли­ентов составляют 660 и 800 тонн продукции ежемесячно. Первый завод мо­жет производить от 400 до 800 тонн, а второй — от 450 до 900 тонн продукции ежемесячно. На первом заводе расходы на производство одной тонны продукции составляют 25, на втором — 28 долл. Сырье для заводов поставляют два поставщика, которые могут поставить не менее 500 тонн сы­рья по цене 200 долл. за тонну первому заводу и не менее 750 тонн по цене 210 долл. второму заводу. Химическая компания предполагает самостоя­тельно транспортировать и сырье, и готовую продукцию. Стоимость транс­портировки одной тонны сырья от первого поставщика к заводам составляет 10 долл. для первого завода и 12 долл. — для второго. Аналогичные стоимо­сти перевозок от второго поставщика равны 9 и 13 долл., соответственно для первого и второго заводов. Стоимость перевозки одной тонны продукции от первого завода к клиентам 1 и 2 составляет 3 и 4, от второго завода — 5 и 2 долл. соответственно. Допустим, из одной тонны сырья можно получить одну тонну готовой продукции. Сформулируйте задачу в виде сетевой модели.

5. В двух открытых школах необходимо изменить расовый баланс среди уча­щихся путем дополнительного их набора из национальных меньшинств. Учащиеся из национальных меньшинств должны составлять от 30 до 40% от общего количества. Учащиеся из национальных меньшинств живут в трех общинах, а "обычные" — в двух. В следующей таблице приведены расстоя­ния от общин до школ (в милях).

Расстояние от школы до

Школа Количество учащихся общины национальных меньшинств "обычной" общины

(не более)
1 1500
2 2000
Количество учащихся
Сформулируйте задачу как	сетевую	модель	и определите расовый	состав

учащихся в каждой школе.

6.5.2. Сетевая модель как задача линейного программирования

Определение модели сети с ограниченной пропускной способностью как задачи линейного программирования необходимо для разработки симплексного алгоритма решения задач данного типа (алгоритм описан в следующем разделе). Используя

Глава 6. Сетевые модели

определения, данные в разделе 6.5.1, мы можем записать задачу линейного програм­мирования для сети с ограниченной пропускной способностью следующим образом.

Минимизировать 2 = ^^]^СЛ

при ограничениях

Z ^хд- Z ^xi=fj> J*^N>

к г

Результирующий "чистый" поток /., протекающий через узел j, вычисляется по формуле

fj = (величина потока, выходящего из узла j) - (величина потока, входящего в узел j).

Узел у выступает в качестве источника, если /_у > 0, и как сток при /_у < 0.

Нижнюю границу пропускной способности l_tj можно удалить из ограничений с помощью подстановки x_tj = х'₀ + 1_1Г Для нового потока x'_v верхней границей пропу­скной способности будет величина u_t. - В этом случае результирующий поток че­рез узел i будет равен f_t -1 , а через узел j — f + На рис. 6.38 показаны преобра­зования характеристик дуги после исключения ее нижней границы пропускной способности.

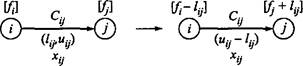
Рис. 6.38. Исключение нижних границ пропускных способностей

Пример 6.5.2

Запишем задачи линейного программирования для сети (см. рис. 6.37) до и после исключения нижних границ пропускных способностей.

Основные ограничения формулируемой задачи линейного программирования свя­заны с определением входных и выходных потоков, протекающих через каждый узел, что порождает следующую задачу ЛП.

	Х2	Х13	Хи	Х23	Х25	Х34	Х35	Х46	Х5в
Минимизировать
Узел 1										= 100
Узел 2	-1									= 200
Узел 3		-1		-1						= 50
Узел 4			-1			-1				= -150
Узел 5					-1		-1			= -80
Узел 6								-1	-1	= -120
Нижние границы
Верхние границы	оо	оо

6.5. Задача нахождения потока наименьшей стоимости

Сделаем замечание о структуре коэффициентов, формирующих ограничения. В столбце, соответствующем переменной х_ц, всегда в строке / стоит +1, а в строке

j--1. Остальные коэффициенты равны нулю. Такая структура коэффициентов

типична для сетевых моделей.

Для переменных, представляющих потоки через дуги, имеющие ненулевые ниж­ние границы пропускных способностей, выполняем замену

^хи ⁼ At + ⁵⁰>

*34 = ^х» + 70,

*₄₆ = x'_v> + 100.

В результате получаем следующую задачу линейного программирования.

	Х12	Х13	At	Х23	Х25	At	X35	Аь	Х56
Минимизировать
Узел 1										= 50
Узел 2	-1									= 200
УзелЗ		-1		-1						= -20
Узел 4			-1			-1				= -130
Узел 5					-1		-1			= -80
Узел 6								-1	-1	= -20
Верхние границы							ОС

Соответствующая сеть после исключения нижних границ пропускных способно­стей дуг показана на рис. 6.39. Отметим, что данную сеть можно получить непо­средственно из сети, представленной на рис. 6.37, с помощью преобразований, по­казанных на рис. 6.38, причем без необходимости записи в виде задачи линейного программирования.

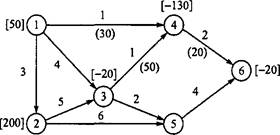
[-80]

Рис. 6.39. Сеть из примера 6.5.2 после исключения нижних границ пропускных способностей

Глава 6. Сетевые модели

Пример 6.5.3. Распределение рабочих

В этом примере представлена сетевая модель, которая изначально не удовлетворяет условию "узлового потока" (т.е. условию, при котором результирующий поток, проходящий через узел, равен разности выходного и входного потоков), но которую можно преобразовать в модель, удовлетворяющую этому условию, изменив огра­ничения соответствующей задачи линейного программирования. Агентство по найму рабочей силы получило заказ на рабочих на 4 месяца вперед (с января по апрель) согласно следующему графику.

Месяц	Январь	Февраль	Март	Апрель
К-во рабочих

Поскольку спрос на рабочих различен в разные месяцы, возможно, экономически целесообразно нанять больше рабочих, чем требуется, в текущем месяце. Стои­мость найма рабочих и удержания их в "ждущем режиме" зависит от времени тру­доустройства, как показано в следующей таблице.

Время трудоустройства (месяцы)
Стоимость найма одного рабочего (долл.)

Обозначим через х количество рабочих, нанятых на начало ('-го месяца и освобож­денных на начало у-го. Например, х₁₂ — это количество рабочих, нанятых в январе только на один месяц.

Чтобы сформулировать задачу линейного программирования, нужно добавить еще пятый месяц (май). Тогда, например, переменная х₁₅ будет обозначать количество ра­бочих, нанятых в апреле на один месяц. Естественно, на май нет заказа на рабочих.

Ограничения строятся так, чтобы спрос на рабочих в месяц к можно было бы удовлетво­рить за счет всех рабочих x_t/, где / < к < j. Обозначив через s, (s, > 0) количество рабочих, "лишних" в месяце /', получим следующую задачу линейного программирования.

	*12	Х13	Х14,	*15	х23	*24	х25	*34	Х35	Х45 S1	S2 S3 Sa
Min
Янв.										-1
Фев.											-1 120
Март											-1 80
Апр.											-1 170

В данной задаче ЛП нет той специальной структуры коэффициентов ограничений, что была в модели из примера 6.5.2. Тем не менее эта задача имеет свою специфику, ко­торая позволит преобразовать ее в сетевую модель. Выполним следующие действия.

1. Из п-го уравнения (ограничения) задачи создадим новое (п + 1)-е уравнение, ум­ножив п-е уравнение на -1.

2. Оставляем первое уравнение без изменений.

3. Для /= 2, 3, п последовательно заменяем г'-е уравнение разностью ;'-го и (/'- 1)-го уравнений.

6.5. Задача нахождения потока наименьшей стоимости

Применение описанной процедуры к задаче данного примера приводит к следующей задаче линейного программирования, которая уже имеет структуру сетевой модели.

	Х12	*13	Х-14	*15	*23	Х24	Х25	Х34	Х35	Х45 S1	S2	S3	S4
Min
Янв.										-1
Фев.	-1										-1
Март		-1			-1							-1		-40
Апр.			-1			-1		-1					-1
Май				-1			-1		-1	-1				-170

Таким образом, задачу распределения рабочих можно представить в виде эквива­лентной задачи вычисления потока минимальной стоимости в сети с ограниченной пропускной способностью (рис. 6.40). Поскольку здесь не налагаются ограничения на верхние границы пропускных способностей, эту задачу можно также решить как транспортную задачу (см. раздел 5.5).

Рис. 6.40. Сеть для примера 6.5.3

УПРАЖНЕНИЯ 6.5.2

1. Сформулируйте задачу линейного программирования, минимизирующую стоимость потока в сети, показанной на рис. 6.41, до и после исключения нижних границ пропускных способностей дуг.

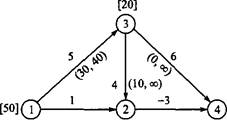
(0, да) (10, оо)

[-40]

Рис. 6.41. Сеть для задачи из упражнения 1

[-30]

Глава 6. Сетевые модели

2. С помощью непосредственной проверки найдите допустимое решение задачи определения потока минимальной стоимости в модели распределения рабо­чих из примера 6.5.3 (см. рис. 6.40). Интерпретируйте найденное решение в терминах первоначальной постановки задачи (как количество нанимаемых рабочих), проверьте выполнение ограничений модели и найдите соответст­вующую общую стоимость.

3. Переформулируйте задачу распределения рабочих (пример 6.5.3), предпола­гая, что рабочие нанимаются не менее, чем на два месяца. Запишите соответ­ствующую задачу линейного программирования и преобразуйте ее в задачу определения потока минимальной стоимости в сети с ограниченной пропуск­ной способностью.

4. Сформулируйте задачи ЛП и соответствующие задачи определения потока минимальной стоимости для модели распределения рабочих из приме­ра 6.5.3, используя следующие данные о потребностях рабочих в течение по­следующих пяти месяцев. Стоимость найма одного рабочего в эти месяцы со­ставит соответственно 50, 70, 85, 100 и 130 долл.

а)

Месяц
К-во рабочих
Ь)
Месяц
К-во рабочих

5. Преобразование сети с ограниченной пропускной способностью в сеть с не­ограниченной пропускной способностью. Покажите, что дугу (i —> j) с ограни­ченным потоком x_tj<u_lt можно заменить двумя дугами, не имеющими огра­ничений на величину потока, — (i -> k) и (k -»j) с результирующим (выходным) потоком [-и ] в узле k и дополнительным (входным) потоком [+и_:/] в узле /'. В результате сеть с ограниченной пропускной способностью преобразуется Тв сеть с неограниченной пропускной способностью, т.е. в транс­портную модель (раздел 5.1). Примените описанное преобразование к сети на рис. 6.42 и найдите оптимальное решение полученной транспортной задачи с помощью программы TORA.

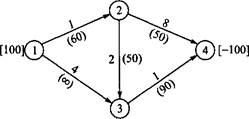
Рис. 6.42. Сеть для задачи из упражнения 5

6.5. Задача нахождения потока наименьшей стоимости

6.5.3. Симплексный алгоритм для сетей с ограниченной пропускной способностью

Предлагаемый алгоритм повторяет в точности те же этапы, что и обычный сим­плекс-метод. Вместе с тем здесь учитывается специальная структура сетевой модели. Используя определения из раздела 6.5.2, где /, — результирующий поток через

узел i, строим симплексный алгоритм на основе условия Z"-i-^ ⁼^ * ^^то У^{словие 03}" начает, что в сети суммарный объем предложений равен суммарному объему спро­са. Мы всегда можем удовлетворить данное условие, введя фиктивный источник или сток, которые можно связать с остальными узлами сети дугами с нулевой стоимостью и бесконечной пропускной способностью. Однако сбалансированность сети не гарантирует существования допустимого решения, поскольку этому может воспрепятствовать ограниченность пропускных способностей дуг.

Опишем алгоритм нахождения потока минимальной стоимости для сетей с ограниченной пропускной способностью. Отметим, что он базируется на стандартном симплекс-методе и теории двойственности (главы 3 и 4). Здесь также полезно знакомст­во с симплекс-методом для задач ЛП с ограниченными переменными (раздел 7.3).

ШагО. Определяем для данной сети начальное базисное допустимое ре­шение (множество дуг). Переходим к шагу 1.

Шаг 1. С помощью условия оптимальности симплекс-метода определяем вводимую в базис переменную (дугу). Если на основе условия оп­тимальности определяем, что последнее решение оптимально, вы­числения заканчиваются. В противном случае переходим к шагу 2.

Шаг 2. На основе условия допустимости симплекс-метода определяем ис­ключаемую из базиса переменную (дугу). Изменив базис, возвра­щаемся к шагу 1.

Сети с п узлами и нулевым результирующим потоком (т.е. при выполнении равенст­ва Д + f₂ + ... + f_n = 0) соответствуют п - 1 независимым ограничениям в виде равенств. Поэтому базисное решение должно содержать п - 1 переменных. Можно показать, что базисное решение соответствует остовному дереву данной сети (см. раздел 6.2).

Вводимая переменная (дуга) на шаге 1 определяется путем вычисления раз­ностей z_tj - c_tj для всех текущих небазисных дуг (t, j). Если для всех разностей z, - c_tj< 0, тогда текущее базисное решение оптимально. Иначе в качестве вводимой в базис переменной выбираем дугу, которой соответствует наибольшее положи­тельное значение разности г_ц - с_ц.

Вычисление разностей z_tj - с_ц основано на соотношениях двойственности точно так же, как в транспортной модели (см. раздел 5.3.4). Обозначим через w_t перемен­ную задачи, двойственной к задаче ЛП (определенной в разделе 6.5.2), которая (переменная) соответствует ограничению узла /. Тогда данная двойственная задача формулируется следующим образом.

Максимизировать z = £/w_i

при выполнении условий

и>,-и>< с_ц, (/, у) е А,

переменные w_t произвольного знака (i = 1, 2, п).

Из теории линейного программирования следует, что w_t - w = с для любой ба­зисной дуги (t, j). Поскольку исходная задача ЛП (раздел 6.5.2) по определению

Глава 6. Сетевые модели

имеет одно избыточное ограничение, мы можем присвоить произвольное значение одной из переменных двойственной задачи (сравните с алгоритмом решения транс­портной задачи из раздела 5.3). Для определенности положим w_x = 0. Затем следует решить (базисную) систему уравнений w_t - w. = c_i;, чтобы вычислить остальные пе­ременные двойственной задачи. Далее находим разности z - с_ц для небазисных пе­ременных согласно формуле

z_l-c_irw-w_rc_lj.

Теперь осталось показать, как определяется исключаемая из базиса переменная. Для этого рассмотрим следующий числовой пример.

Пример 6.5.4

Сеть трубопроводов связывает две станции опреснения воды с двумя городами. Ежедневное предложение опреснительных станций составляет 40 и 50 миллионов галлонов воды, города ежедневно потребляют 30 и 60 миллионов галлонов воды. Каждая станция трубопроводами соединена с каждым городом непосредственно, однако они могут также перекачивать воду в города через специальную насосную станцию. Кроме того, станция 1 может транспортировать воду на станцию 2, а го­род 1 — в город 2. Данная сеть сбалансирована, так как в ней суммарный спрос ра­вен суммарному предложению. Описанная сеть показана на рис. 6.43.

Удельная стоимость Пропускная способность

Рис. 6.43. Сеть для примера 6.5.4

Определение начального допустимого базисного решения. Нетруд­но построить остовное дерево (на рис. 6.44 показано сплошными дугами) для рассматриваемой сети. Отсюда получаем начальное допустимое базисное решение. Обычно, чтобы найти такое реше­ние, используется метод введения искусственных переменных (подробности см. в [2]).

На рис. 6.44 показано, что базисному решению соответствуют дуги (1, 3), (1, 4), (2, 3) и (3, 5) с потоками 30, 10, 50 и 60 единиц соот­ветственно. Оставшиеся дуги (показаны пунктиром) представляют небазисные переменные. Запись х(с) показывает, что через соот­ветствующую дугу с пропускной способностью с проходит поток х. По умолчанию считается, что х = 0 и с = со.

Итерация 0 Шаг 0.

6.5. Задача нахождения потока наименьшей стоимости

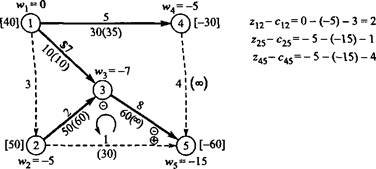
= 9

= 6

Рис. 6.44. Сеть на итерации О

Итерация 1

Шаг 1. Определение вводимой в базис переменной. При решении системы уравнений

w, = 0,

w, - w_j = c_Lj для базисных дуг получим значения переменных двойственной задачи.

Дуга (1, 3): w, - w₃ = 7 w₃ = -7.

Дуга (1, 4): w, - w_t = 5 w₄ = -5.

Дуга (2, 3): w₂ - w₃ = 2 w₂ = -5.

Дуга (3, 5): w₃ - w₅ = 8 => w_b = -15. Теперь вычисляем разности z,. - с . для небазисных переменных.

Дуга (1, 2): w, - w₂ - с₁₂ = 0 - (-5) -3 = 2.

Дуга (2, 5): w₂ - w₅ - с₂₅ = (-5) - (-15) -1 = 9.

Дуга (4, 5): w_t - w₅ - с_4б = (-5) - (-15) -4 = 6.

Таким образом, дуга (2, 5) будет введена в базисное решение.

Шаг 2. Определение исключаемой из базиса переменной. На рис. 6.44 видно, что дуга (2, 5) совместно с базисными дугами (2, 3) и (3, 5) образует цикл. По определению остовное дерево не может содер­жать циклов. Поскольку поток через дугу (2, 5) должен возрасти, необходимо выровнять потоки через дуги, составляющие цикл та­ким образом, чтобы новое решение осталось допустимым. Для это­го поток через дугу (2, 5) пометим знаком "+", потоки через дру­гие дуги цикла— знаком "+" или в зависимости от того, будут ли совпадать направления потоков в этих дугах с направле­нием потока в дуге (2, 5) при обходе цикла против часовой стрел­ки.⁵ Пометки дуг цикла показаны на рис. 6.44. При определении максимального потока, протекающего через ду­гу (2, 5), необходимо придерживаться следующих правил.

⁵ Направление обхода дуг цикла всегда совпадает с направлением потока, протекающего через дугу, вводимую в базис. В данном случае это направление совпадает с направлением против часовой стрелки, но это, конечно, совсем не обязательно. — Прим. ред.

Глава 6. Сетевые модели

1. Новый поток в текущей базисной дуге не может быть отрицательным.

2. Поток через вводимую в базис дугу не может превышать ее пропускную способность.

Применение правила 1 показывает, что потоки через дуги (2, 3) и (3, 5) нельзя уменьшить более, чем на min{50, 60} = 50 единиц. Из правила 2 следует, что поток через дугу (2, 5) не может превышать 30 единиц (пропускная способность этой дуги равна 30). Поэтому поток через дуги цикла изменится не более, чем на min{30, 50} = 30 единиц. Таким образом, поток через дугу (2, 5) равен 30 единиц, через дугу (2, 3) 50 - 30 = 20 единиц, а через дугу (3, 5) — 60 - 30 = 30 единиц.

Поскольку никакая из текущих базисных переменных не приняла нулевого значения, дуга (2, 5) должна остаться небазисной, но с ненулевым значением в 30 единиц. Чтобы выполнить требование равенства нулю небазисных перемен­ных, сделаем подстановку

*₂₅ = 30 -х₅₂,0<х₅₂<30. Эта подстановка изменит уравнения для потоков, протекающих через узлы 2 и 5.

Текущее уравнение для потоков узла 2: 50 + х_]2 = х₂₃ + х_2Ъ.

Текущее уравнение для потоков узла 5: х_2ь + х₃₅ + х₄₅ = 60. После подстановки х_2Ъ — 30 - х_Ь2 получим следующее.

Новое уравнение для потоков узла 2: 20 + х₁₂ + х₅₂= х₂₃.

Новое уравнение для потоков узла 5: х₃₅ + x_i5 = х₅₂ + 30.

Результаты этих изменений показаны на рис. 6.45. Направление потока через дугу (2, 5) изменилось на обратное (от узла 5 к узлу 2), причем, как и ожидалось, х_Ь2 = 0. Описанная подстановка также требует изменения стоимости прохождения потока по дуге (2, 5) до -1 долл. Те дуги, направления потоков которых изменены на про­тивоположные, помечены в сети звездочкой.

w, = 0 w₄ = -5

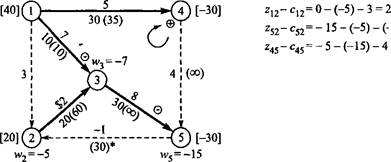
-1) = -9 = 6

Рис. 6.45. Сеть на итерации 1

Итерация 2. На рис. 6.45 представлены новые значения разностей z,. - с_ц (проверьте эти значения!). Очевидно, что в базис следует ввести дугу (4, 5). Введение в базис этой дуги также приводит к образованию цикла.

Величину потока через дугу (4, 5) можно увеличить до наименьшей из следующих величин.

6.5. Задача нахождения потока наименьшей стоимости

1. Максимальный поток через дугу (4, 5), определяемый пропускной способно­стью, равен со.

2. Максимальное увеличение потока через дугу (1, 4) равно 35 - 30 = 5 единиц.

3. Максимальное уменьшение потока через дугу (1, 3) равно 10 единиц.

4. Максимальное уменьшение потока через дугу (3, 5) равно 30 единиц.

Таким образом, поток через дугу (4, 5) можно увеличить до 5 единиц; эта дуга вхо­дит в базис, а дуга (1, 4) с потоком в 35 единиц исключается из базиса.

Выполнив подстановку х_ы = 35 - х₄₁, получим сеть, показанную на рис. 6.46, где ду­ги (1, 3), (2, 3), (3, 5) и (4, 5) формируют остовное дерево сети (базисное решение). Для дуги (1, 4) с обратным направлением потока изменена стоимость прохождения потока до -5 долл. Проверьте самостоятельно, что в уравнения для потоков в узлах 1 и 4 будет добавлено 5 единиц входного потока.

<4)[5]

5(оо)

42 *-12 ^z41 ~ ^с41⁼

*52^-t-52"

с,,-0-(-5)-3-2

11 - 0 - (-5) = -6 15-(-5)-(-1) = -9

[-30]

Рис. 6.46. Сеть на итерации 2

Итерация 3. Вычисленные новые значения разностей z, - с, для небазисных дуг (1, 2), (4, 1) и (5, 2) показаны на рис. 6.46. Из этих значений вытекает, что в базис следует ввести дугу (1, 2) с потоком в 5 единиц, тогда как дуга (1, 3) исключается из базиса с нулевым значением потока. Новое решение представлено на рис. 6.47.

w, = 0

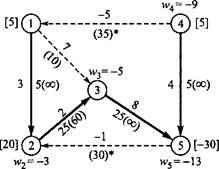
*41 Ml'

= 0-(-5)-7 = -:_₉_0-(-5) =

-4

^52 ^ь52

с₅₂=-13-(-3)-(-1) = -9

Оптимальное решение:

^;5, *1₃=0 ■ 35 -0 = 35

х₂₃=25

х„=30-0 = 30

*25

*35^:

= 25, х,

45"

Суммарная стоимость = 490 Рис. 6.47. Сеть на итерации 3

Итерация 4. Из новых значений разностей г_ц - c_tj (рис. 6.47) видно, что последнее решение оптимально. Значения исходных переменных получаем путем обратной подстановки, как показано на рис. 6.47.

Глава 6. Сетевые модели

УПРАЖНЕНИЯ 6.5.3

1. Решите задачу из упражнения 6.5.1.1 с помощью симплексного алгоритма для сетей с ограниченной пропускной способностью. Покажите также, что эту задачу можно решить как транспортную.

2. Решите задачу из упражнения 6.5.1.2 с помощью симплексного алгоритма для сетей с ограниченной пропускной способностью. Покажите также, что эту задачу можно решить как транспортную.

3. Решите задачу из упражнения 6.5.1.3 с помощью симплексного алгоритма для сетей с ограниченной пропускной способностью.

4. Решите задачу из упражнения 6.5.1.4 с помощью симплексного алгоритма для сетей с ограниченной пропускной способностью.

5. Решите задачу из упражнения 6.5.1.5 с помощью симплексного алгоритма для сетей с ограниченной пропускной способностью.

6. Решите задачу из примера 6.5.3 с помощью симплексного алгоритма для се­тей с ограниченной пропускной способностью.

7. Электрическая компания Вайоминга транспортирует по трубопроводам угольную пульпу от трех шахт (1, 2 и 3) к трем электростанциям (4, 5 и 6). Каждый трубопровод может транспортировать не более 10 тонн пульпы в час. Стоимость транспортировки одной тонны пульпы (в долл.), а также предложе­ние шахт и спрос электростанций представлены в следующей таблице.

4 5 6 Предложение

Спрос 16 6 14

Найдите оптимальную схему транспортировки угля к электростанциям.

8. На рис. 6.48 показана сеть из семи городов и расстояния между ними. С по­мощью симплексного алгоритма для сетей с ограниченной пропускной спо­собностью найдите кратчайший маршрут между городами 1 и 7. (Совет. Пусть узлы 1 и 7 имеют результирующие потоки [+1] и [-1] соответственно, а все остальные — нулевые результирующие потоки.)

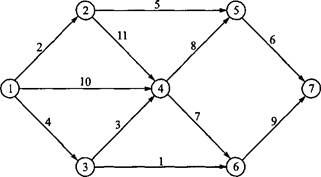
Рис. 6.48. Сеть для задачи из упражнения 8

6.5. Задача нахождения потока наименьшей стоимости

9. Покажите, что симплексный алгоритм вычисления потока минимальной стоимости для сетей с ограниченной пропускной способностью можно при­менить, чтобы найти максимальный поток в сети (см. раздел 6.4). С его по­мощью решите задачу из примера 6.4.2. Для определенности положите стоимость прохождения потока от узла 4 к узлу 3 нулевой, остальные данные остаются без изменений.

6.5.4. Решение задачи вычисления потока наименьшей стоимости в Excel

Шаблон Excel, предназначенный для решения общей транспортной задачи (см. раздел 5.3.3), можно применить, чтобы найти поток наименьшей стоимости. На рис. 6.49 показан рабочий лист, на котором решается задача из примера 6.5.4 (файл

2 Входные длины»

В С Е F G Н