рефераты конспекты курсовые дипломные лекции шпоры
- Раздел Математика
- /
- Линейные геометрические объекты.
Реферат Курсовая Конспект
Линейные геометрические объекты.
Линейные геометрические объекты. - раздел Математика, Линейная алгебра Определение.Пусть ...
Определение.Пусть  есть некоторый ненулевой вектор, а
есть некоторый ненулевой вектор, а  - произвольный вектор из
- произвольный вектор из  . Множество элементов линейного пространства
. Множество элементов линейного пространства  вида
вида 
 , где параметр
, где параметр  пробегает множество вещественных чисел, называют прямой проходящей через точку
пробегает множество вещественных чисел, называют прямой проходящей через точку  по направлению вектора
по направлению вектора  .
.
При  прямая проходит через нулевой вектор пространства
прямая проходит через нулевой вектор пространства  и представляет собой линейную оболочку направляющего вектора
и представляет собой линейную оболочку направляющего вектора  . Как и любая линейная оболочка эта прямая является линейным подпространством. Размерность этого подпространства равна единице, так как любой вектор может быть представлен в виде разложения по одному вектору
. Как и любая линейная оболочка эта прямая является линейным подпространством. Размерность этого подпространства равна единице, так как любой вектор может быть представлен в виде разложения по одному вектору  , а любые два вектора такой прямой линейно зависимы.
, а любые два вектора такой прямой линейно зависимы.
В общем случае, при  , прямая получается из линейного подпространства сдвигом на вектор
, прямая получается из линейного подпространства сдвигом на вектор  .
.
Определение.Любое подмножество линейного пространства, полученное путем сдвига на некоторый фиксированный вектор, называют линейным многообразием. При этом размерность линейного многообразия считают равной размерности исходного подпространства.
Таким образом, прямая в линейном пространстве является одномерным линейным многообразием.
В реальном пространстве трехмерных арифметических векторов (точек) прямая задается векторно-параметрическим уравнением  , где
, где  - компоненты произвольной точки на прямой,
- компоненты произвольной точки на прямой,  - компоненты некоторой фиксированной точки на прямой,
- компоненты некоторой фиксированной точки на прямой,  - компоненты направляющего вектора,
- компоненты направляющего вектора,  - параметр.
- параметр.
Если прямую задают с помощью геометрических векторов, то ее определяют как множество точек в реальном пространстве, задаваемых уравнением в векторно-параметрической форме 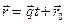 , где
, где  - радиус-вектор произвольной точки
- радиус-вектор произвольной точки 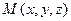 на прямой,
на прямой,  - радиус-вектор некоторой выбранной точки
- радиус-вектор некоторой выбранной точки 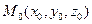 на прямой,
на прямой,  - направляющий геометрический вектор.
- направляющий геометрический вектор.
Представив векторно-параметрическое уравнение прямой в реальном пространстве в покомпонентной записи, получаем три скалярных уравнения
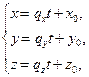
которые называются параметрическими уравнениями прямой.
Разрешая, полученные параметрические уравнения, относительно параметра  и приравнивая полученные соотношения, приходим к каноническим уравнениям прямой
и приравнивая полученные соотношения, приходим к каноническим уравнениям прямой
 .
.
Замечание.Если одна или две компоненты направляющего вектора прямой равны нулю, то канонические уравнения принято записывать в символической форме, сохраняя нули в знаменателях.
Пример. Пусть некоторая прямая в реальном пространстве задана параметрическими уравнениями вида 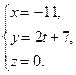 Тогда символическая запись канонических уравнений в виде
Тогда символическая запись канонических уравнений в виде  означает, что данная прямая проходит через точку
означает, что данная прямая проходит через точку 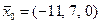 по направлению вектора
по направлению вектора  .
.
Определение.Две любые прямые  и
и  линейного пространства называются параллельными, если их направляющие векторы
линейного пространства называются параллельными, если их направляющие векторы  и
и  являются коллинеарными.
являются коллинеарными.
Пример. Пусть прямая  имеет векторное уравнение
имеет векторное уравнение , а прямая
, а прямая  имеет векторное уравнение
имеет векторное уравнение . По определению эти прямые являются параллельными, так как направляющий вектор второй прямой
. По определению эти прямые являются параллельными, так как направляющий вектор второй прямой  линейно выражается через направляющий вектор первой прямой
линейно выражается через направляющий вектор первой прямой  по формуле
по формуле 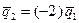 , что позволяет считать направляющие векторы
, что позволяет считать направляющие векторы  и
и  коллинеарными.
коллинеарными.
Определение.Две любые прямые  и
и  евклидова пространства называются перпендикулярными, если их направляющие векторы
евклидова пространства называются перпендикулярными, если их направляющие векторы  и
и  являются ортогональными.
являются ортогональными.
В частности, если прямые  и
и  заданы в реальном пространстве, то их направляющие векторы имеют, например, вид
заданы в реальном пространстве, то их направляющие векторы имеют, например, вид  и
и  . По определению эти прямые перпендикулярны, когда скалярное произведение их направляющих векторов равно нулю, т.е.
. По определению эти прямые перпендикулярны, когда скалярное произведение их направляющих векторов равно нулю, т.е.  Аналогично, если прямые
Аналогично, если прямые  и
и  заданы на плоскости, то их направляющие векторы имеют вид
заданы на плоскости, то их направляющие векторы имеют вид  и
и  , а условие их перпендикулярности задается равенствами
, а условие их перпендикулярности задается равенствами 
Пример. Пусть прямая  на плоскости задана уравнением с угловым коэффициентом в виде
на плоскости задана уравнением с угловым коэффициентом в виде . Ее параметрические уравнения можно записать в виде:
. Ее параметрические уравнения можно записать в виде: 
Отсюда направляющий вектор этой прямой равен 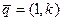 и прямая
и прямая  проходит через точку
проходит через точку  . Найдем прямую
. Найдем прямую  , проходящую через ту же точку
, проходящую через ту же точку  , перпендикулярно первой прямой
, перпендикулярно первой прямой  . Направляющий вектор
. Направляющий вектор 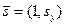 прямой
прямой  будем искать из условия перпендикулярности прямых, так что:
будем искать из условия перпендикулярности прямых, так что:  .
.
Таким образом, параметрические уравнения прямой  можно записать в виде
можно записать в виде 
а ее уравнение с угловым коэффициентом будет иметь вид  .
.
Определение.Угол между любыми прямыми  и
и  евклидова пространства определяется как наименьший угол между их направляющими векторами
евклидова пространства определяется как наименьший угол между их направляющими векторами  и
и 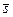 , и вычисляется по формуле
, и вычисляется по формуле  .
.
В частности, если прямые  и
и  заданы в реальном пространстве, то их направляющие векторы имеют вид
заданы в реальном пространстве, то их направляющие векторы имеют вид  и
и  .
.
По определению, угол между прямыми  и
и  рассчитывается по формуле:
рассчитывается по формуле:
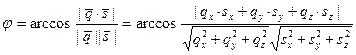 .
.
Пример. Пусть прямые  и
и  на плоскости заданы уравнениями с угловым коэффициентом в виде
на плоскости заданы уравнениями с угловым коэффициентом в виде и
и 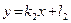 . Направляющий вектор первой прямой равен
. Направляющий вектор первой прямой равен  и прямая проходит через точку
и прямая проходит через точку  Направляющий вектор второй прямой равен
Направляющий вектор второй прямой равен  и прямая проходит через точку
и прямая проходит через точку  По определению, угол между этими прямыми рассчитывается по формуле
По определению, угол между этими прямыми рассчитывается по формуле  . Часто, пользуясь приведенной выше формулой, угол между двумя прямыми на плоскости выражают с помощью функции арктангенса по формуле
. Часто, пользуясь приведенной выше формулой, угол между двумя прямыми на плоскости выражают с помощью функции арктангенса по формуле  .
.
Отметим также, что векторы  и
и  являются коллинеарными только в том случае, когда их вторые компоненты равны, т.е.
являются коллинеарными только в том случае, когда их вторые компоненты равны, т.е. 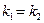 . Отсюда следует, что прямые
. Отсюда следует, что прямые  и
и 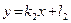 , заданные уравнениями с угловым коэффициентом, параллельны, когда их угловые коэффициенты равны.
, заданные уравнениями с угловым коэффициентом, параллельны, когда их угловые коэффициенты равны.
Через любые две различные точки 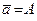 и
и  векторного пространства
векторного пространства  проходит одна и только одна прямая. Единственная прямая, проходящая через точки
проходит одна и только одна прямая. Единственная прямая, проходящая через точки 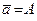 и
и  , находится из общего уравнения прямой
, находится из общего уравнения прямой  , и записывается в виде
, и записывается в виде  при векторно-параметрической форме записи, или в виде
при векторно-параметрической форме записи, или в виде  при точечной интерпретации арифметических векторов. Отметим, что при
при точечной интерпретации арифметических векторов. Отметим, что при  получаем
получаем  , а при
, а при  имеем
имеем 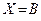 .
.
Определение.Множество точек 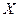 линейного пространства
линейного пространства  , задаваемых с помощью равенства вида
, задаваемых с помощью равенства вида  называют отрезком, соединяющим точки
называют отрезком, соединяющим точки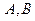 , и обозначают
, и обозначают .
.
В частности, в реальном пространстве отрезок  задается при параметре
задается при параметре  с помощью параметрических уравнений
с помощью параметрических уравнений  где точка
где точка  является левой границей отрезка, а точка
является левой границей отрезка, а точка  есть правая граница отрезка.
есть правая граница отрезка.
Определение. Точка 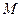 отрезка
отрезка делит его в отношении
делит его в отношении  , если для направленных отрезков
, если для направленных отрезков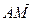 ,
, 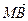 выполняется равенство
выполняется равенство  .
.
Для нахождения точки 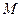 решается векторное уравнение
решается векторное уравнение  , равносильное уравнению
, равносильное уравнению  , о котором говорится в определении точки деления
, о котором говорится в определении точки деления 
В точечно-векторной записи получаем решение  . Отсюда компоненты точки
. Отсюда компоненты точки 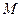 вычисляются по формулам
вычисляются по формулам 
Если по условию задачи задано отношение  , то из предшествующих формул следует, что точка
, то из предшествующих формул следует, что точка 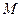 находится по формуле
находится по формуле  , а компоненты точки
, а компоненты точки 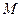 вычисляются по формулам
вычисляются по формулам 
Сравнивая последние формулы с определением отрезка, получаем, что точка 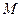 находится из уравнения отрезка при условии, что параметр
находится из уравнения отрезка при условии, что параметр  равен значению
равен значению 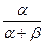 .
.
Если, в частности, требуется разделить отрезок в отношении  , то изо всех приведенных формул следует, что точка
, то изо всех приведенных формул следует, что точка 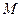 лежит в центре отрезка и равна
лежит в центре отрезка и равна  .
.
Определение.Пусть 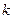 есть некоторое натуральное число, строго меньшее, чем размерность
есть некоторое натуральное число, строго меньшее, чем размерность  векторного пространства
векторного пространства  . Множество векторов линейного пространства вида
. Множество векторов линейного пространства вида 
 называют
называют 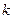 -мерной плоскостью, проходящей через вектор
-мерной плоскостью, проходящей через вектор  , если
, если  - некоторый фиксированный вектор, параметры
- некоторый фиксированный вектор, параметры  независимо друг от друга пробегают множество вещественных чисел, векторы
независимо друг от друга пробегают множество вещественных чисел, векторы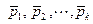 образуют систему линейно независимых векторов.
образуют систему линейно независимых векторов.
При  плоскость проходит через нулевой вектор пространства
плоскость проходит через нулевой вектор пространства  и представляет собой линейную оболочку линейно независимых векторов
и представляет собой линейную оболочку линейно независимых векторов 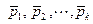 . Как и любая линейная оболочка, плоскость, проходящая через нулевой вектор, является линейным подпространством. Размерность этого подпространства равна
. Как и любая линейная оболочка, плоскость, проходящая через нулевой вектор, является линейным подпространством. Размерность этого подпространства равна 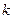 , так как любой вектор такой плоскости может быть представлен в виде разложения по векторам
, так как любой вектор такой плоскости может быть представлен в виде разложения по векторам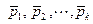 .
.
В общем случае, если  ,
, 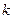 -мерная плоскость получается из линейной оболочки, натянутой на векторы
-мерная плоскость получается из линейной оболочки, натянутой на векторы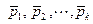 , сдвигом на вектор
, сдвигом на вектор  .
.
Таким образом, можно сказать, что 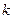 -мерная плоскость в линейном пространстве
-мерная плоскость в линейном пространстве  является
является 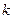 -мерным линейным многообразием.
-мерным линейным многообразием.
Одномерные плоскости есть определенные ранее прямые. Плоскости размерности 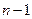 называются гиперплоскостями.
называются гиперплоскостями.
В реальном пространстве трехмерных арифметических векторов (точек) плоскость размерности два совпадает с гиперплоскостью, и обычно называется плоскостью.
Определение.Множество точек реального пространства вида 
 называют плоскостью, проходящей через точку
называют плоскостью, проходящей через точку  , если
, если  - некоторая фиксированная точка, параметры
- некоторая фиксированная точка, параметры 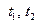 независимо друг от друга пробегают множество вещественных чисел, арифметические векторы
независимо друг от друга пробегают множество вещественных чисел, арифметические векторы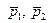 образуют систему линейно независимых векторов.
образуют систему линейно независимых векторов.
Реальное пространство имеет размерность три и является, по определению, пространством со скалярным произведением, т.е. является евклидовым пространством. Тогда для двух линейно независимых векторов 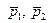 , задающих направление плоскости, можно, используя алгоритм Грамма-Шмидта, построить третий ненулевой вектор
, задающих направление плоскости, можно, используя алгоритм Грамма-Шмидта, построить третий ненулевой вектор  , ортогональный им, таким образом, чтобы
, ортогональный им, таким образом, чтобы  и
и  .
.
Определение.Плоскость  в реальном трехмерном пространстве задается с помощью векторно-точечного уравнения
в реальном трехмерном пространстве задается с помощью векторно-точечного уравнения  , где
, где  есть произвольный арифметический вектор (произвольная точка
есть произвольный арифметический вектор (произвольная точка  на плоскости),
на плоскости),  есть некоторый фиксированный арифметический вектор (фиксированная точка
есть некоторый фиксированный арифметический вектор (фиксированная точка  на плоскости),
на плоскости),  есть ненулевой, нормальный вектор.
есть ненулевой, нормальный вектор.
Если плоскость  задают с помощью геометрических векторов, то ее определяют как множество точек в реальном пространстве, задаваемых уравнением плоскости в векторной форме
задают с помощью геометрических векторов, то ее определяют как множество точек в реальном пространстве, задаваемых уравнением плоскости в векторной форме 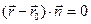 , где
, где  - радиус-вектор произвольной точки
- радиус-вектор произвольной точки  на плоскости,
на плоскости,  - радиус-вектор некоторой выбранной точки
- радиус-вектор некоторой выбранной точки  на плоскости,
на плоскости,  - нормальный геометрический вектор.
- нормальный геометрический вектор.
Зададим векторно-параметрическое уравнение плоскости в реальном пространстве в покомпонентной записи. Полученное уравнение  , переписанное в стандартных буквенных обозначениях
, переписанное в стандартных буквенных обозначениях 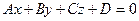 , называют общим уравнением плоскости.Отметим, что коэффициенты
, называют общим уравнением плоскости.Отметим, что коэффициенты 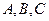 , стоящие в общем уравнении плоскости при переменных
, стоящие в общем уравнении плоскости при переменных  , являются компонентами нормального вектора, т.е.
, являются компонентами нормального вектора, т.е.  .
.
Пример. Пусть некоторая плоскость  в реальном пространстве задана общим уравнением
в реальном пространстве задана общим уравнением  . Тогда нормальный вектор плоскости имеет вид
. Тогда нормальный вектор плоскости имеет вид  , его направляющие косинусы имеют значения
, его направляющие косинусы имеют значения  , а любая точка плоскости находится из общего уравнения, например, в виде
, а любая точка плоскости находится из общего уравнения, например, в виде 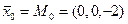 .
.
С помощью векторно-точечного уравнения  наша плоскость может быть задана в виде
наша плоскость может быть задана в виде 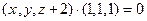 .
.
Определение.Две любые плоскости  и
и 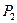 реального пространства называются параллельными, если их нормальные векторы
реального пространства называются параллельными, если их нормальные векторы 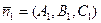 и
и  являются коллинеарными. Если оба нормальных вектора имеют отличные от нуля компоненты, то условие параллельности плоскостей имеет вид
являются коллинеарными. Если оба нормальных вектора имеют отличные от нуля компоненты, то условие параллельности плоскостей имеет вид  .
.
Пример. Пусть плоскость  задана общим уравнением
задана общим уравнением 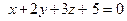 , а плоскость
, а плоскость 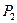 задана векторным уравнением
задана векторным уравнением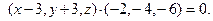 По определению эти плоскости являются параллельными, так как нормальный вектор второй плоскости
По определению эти плоскости являются параллельными, так как нормальный вектор второй плоскости  линейно выражается через нормальный вектор первой плоскости
линейно выражается через нормальный вектор первой плоскости  по формуле
по формуле 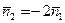 , что позволяет считать направляющие векторы
, что позволяет считать направляющие векторы  коллинеарными.
коллинеарными.
Определение.Две любые плоскости  и
и 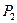 реального пространства называются перпендикулярными, если их нормальные векторы
реального пространства называются перпендикулярными, если их нормальные векторы  и
и  являются ортогональными, т.е. их скалярное произведение равно нулю
являются ортогональными, т.е. их скалярное произведение равно нулю  .
.
Пример. Пусть плоскость  задана общим уравнением
задана общим уравнением 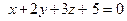 , а плоскость
, а плоскость 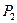 задана векторным уравнением
задана векторным уравнением По определению эти плоскости являются перпендикулярными, так как скалярное произведение их нормальных векторов равно нулю
По определению эти плоскости являются перпендикулярными, так как скалярное произведение их нормальных векторов равно нулю  , т.е. векторы
, т.е. векторы  - ортогональны.
- ортогональны.
Определение.Угол между любыми плоскости  и
и 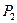 реального пространства определяется как меньший угол между их нормальными векторами
реального пространства определяется как меньший угол между их нормальными векторами  и
и  , и вычисляется по формуле
, и вычисляется по формуле  .
.
Пример. Пусть требуется провести плоскость  через некоторую фиксированную точку
через некоторую фиксированную точку  параллельно двум неколлинеарным векторам
параллельно двум неколлинеарным векторам  и
и  . Так как векторы
. Так как векторы и
и  по условию являются неколлинеарными, то их векторное произведение
по условию являются неколлинеарными, то их векторное произведение равно некоторому ненулевому вектору, который перпендикулярен обоим векторам
равно некоторому ненулевому вектору, который перпендикулярен обоим векторам  и
и  . Поэтому нормальный вектор плоскости
. Поэтому нормальный вектор плоскости  можно выбрать равным
можно выбрать равным  , т.е.
, т.е. 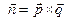 .
.
Обозначим  произвольную точку плоскости. Направленный отрезок
произвольную точку плоскости. Направленный отрезок 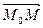 лежит в искомой плоскости. Отсюда следует, что векторное уравнение
лежит в искомой плоскости. Отсюда следует, что векторное уравнение  задает искомую плоскость
задает искомую плоскость  . Подставляя в уравнение вместо вектора
. Подставляя в уравнение вместо вектора  равный ему вектор
равный ему вектор  , получим уравнение
, получим уравнение  , где в левой части стоит смешанное произведение векторов. Если в полученное векторное уравнение подставить компоненты векторов, то уравнение плоскости находят, раскрывая определитель
, где в левой части стоит смешанное произведение векторов. Если в полученное векторное уравнение подставить компоненты векторов, то уравнение плоскости находят, раскрывая определитель  .
.
В частности, пусть требуется провести плоскость  через точку
через точку 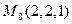 параллельно двум неколлинеарным векторам
параллельно двум неколлинеарным векторам  и
и  .
.
Подставляя данные примера в выведенное уравнение с определителем, получим
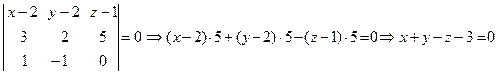 .
.
Пример. Составим уравнение плоскости, проходящей через три точки  ,
,  ,
, 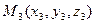 , не лежащие на одной прямой. Обозначим
, не лежащие на одной прямой. Обозначим  произвольную точку плоскости. Направленные отрезки
произвольную точку плоскости. Направленные отрезки  ,
,  ,
,  лежат в искомой плоскости. Так как точки
лежат в искомой плоскости. Так как точки  ,
,  ,
, 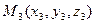 не лежат на одной прямой, то векторы
не лежат на одной прямой, то векторы  ,
,  являются неколлинеарными. Их векторное произведение
являются неколлинеарными. Их векторное произведение  равно некоторому ненулевому вектору, который перпендикулярен обоим векторам
равно некоторому ненулевому вектору, который перпендикулярен обоим векторам  ,
,  , и может рассматриваться как нормальный вектор плоскости.
, и может рассматриваться как нормальный вектор плоскости.
По аналогии с предшествующей задачей, уравнение искомой плоскости можно найти, раскрывая определитель  .
.
В частности, составим уравнение плоскости, проходящей через три точки  ,
,  ,
,  .
.
Подставляя координаты точек в уравнение с определителем в левой части, получим
 .
.
Определение.Углом  между прямой
между прямой  и плоскостью
и плоскостью  в реальном пространстве называется меньший угол между прямой и ее проекцией на плоскость.
в реальном пространстве называется меньший угол между прямой и ее проекцией на плоскость.
Для определения угла между прямой и плоскостью используется направляющий вектор прямой  и нормальный вектор плоскости
и нормальный вектор плоскости , а сам угол
, а сам угол  вычисляется по формуле
вычисляется по формуле
 .
.
Пример. Вычислим угол между прямой 
заданной как пересечение двух плоскостей, и плоскостью  , заданной уравнением в общем виде
, заданной уравнением в общем виде  .
.
Направляющий вектор 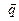 прямой
прямой  найдем как векторное произведение нормального вектора
найдем как векторное произведение нормального вектора  первой плоскости
первой плоскости  и нормального вектора
и нормального вектора  второй плоскости
второй плоскости 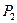
 .
.
Отсюда, по формуле находим угол  между прямой
между прямой  и плоскостью
и плоскостью 
 .
.
Пример. Найти ортогональную проекцию  некоторой точки
некоторой точки  на плоскость
на плоскость  и расстояние от точки
и расстояние от точки  до плоскости
до плоскости  .
.
Под ортогональной проекцией точки на плоскость понимают точку пересечения прямой, перпендикулярной к плоскости, с указанной плоскостью. Расстояние от точки до плоскости находят как расстояние от точки  до точки
до точки  .
.
Если прямая  перпендикулярна плоскости
перпендикулярна плоскости  , то ее направляющий вектор может быть выбран равным нормальному вектору
, то ее направляющий вектор может быть выбран равным нормальному вектору  плоскости
плоскости  . Запишем уравнение прямой
. Запишем уравнение прямой  , проходящей через точку
, проходящей через точку  , в виде
, в виде  С тем, чтобы найти точку
С тем, чтобы найти точку  пересечения прямой
пересечения прямой  с плоскостью
с плоскостью  , подставим параметрические уравнения прямой в плоскость. В результате получим следующее линейное уравнение относительно параметра
, подставим параметрические уравнения прямой в плоскость. В результате получим следующее линейное уравнение относительно параметра  :
: 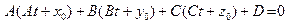 . Отсюда находится значение параметра
. Отсюда находится значение параметра  , соответствующее ортогональной проекции
, соответствующее ортогональной проекции  , и координаты точки
, и координаты точки  в следующем виде:
в следующем виде:  ,
, 
Расстояние между точками  и
и  равно длине направленного отрезка
равно длине направленного отрезка  и вычисляется по формуле
и вычисляется по формуле  .
.
В частности, найдем проекцию точки  на плоскость
на плоскость 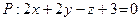 и расстояние от точки
и расстояние от точки  до плоскости
до плоскости  .
.
В соответствии с общими формулами:
 ,
,
 .
.
Пример. Найти ортогональную проекцию  некоторой точки
некоторой точки  на прямую
на прямую  и расстояние от точки
и расстояние от точки  до прямой
до прямой  .
.
Под ортогональной проекцией  точки на прямую понимают точку пересечения плоскости
точки на прямую понимают точку пересечения плоскости  , перпендикулярной к исходной прямой, с исходной прямой. Расстояние от точки до прямой находят как расстояние от точки
, перпендикулярной к исходной прямой, с исходной прямой. Расстояние от точки до прямой находят как расстояние от точки  до точки
до точки  .
.
Если плоскость  перпендикулярна прямой
перпендикулярна прямой  , то нормальный вектор плоскости может быть выбран равным направляющему вектору
, то нормальный вектор плоскости может быть выбран равным направляющему вектору  исходной прямой
исходной прямой  .
.
Запишем уравнение плоскости  , перпендикулярной к исходной прямой, и проходящей через точку
, перпендикулярной к исходной прямой, и проходящей через точку  , в виде
, в виде  . Чтобы найти точку
. Чтобы найти точку  пересечения плоскости
пересечения плоскости  с прямой
с прямой  , подставим параметрические уравнения прямой в плоскость.
, подставим параметрические уравнения прямой в плоскость.
В результате получим следующее линейное уравнение относительно параметра  :
: 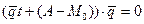 .
.
Отсюда находится значение параметра  , соответствующее ортогональной проекции
, соответствующее ортогональной проекции  , и координаты точки
, и координаты точки  в следующем виде:
в следующем виде: 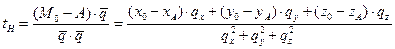 ,
, 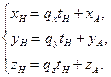
Расстояние между точками  и
и  равно длине направленного отрезка
равно длине направленного отрезка  и вычисляется по формуле
и вычисляется по формуле 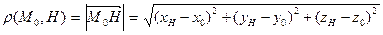 .
.
В частности, найдем проекцию точки  на прямую
на прямую  и расстояние от точки
и расстояние от точки  до плоскости
до плоскости  . В соответствии с общими формулами:
. В соответствии с общими формулами:
 ,
,
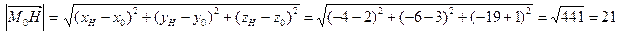 .
.
– Конец работы –
Эта тема принадлежит разделу:
Линейная алгебра
На сайте allrefs.net читайте: "Линейная алгебра"
Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Линейные геометрические объекты.
Что будем делать с полученным материалом:
Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:
| Твитнуть |
Хотите получать на электронную почту самые свежие новости?






Новости и инфо для студентов