Метод Гауса з послідовним виключенням невідомих

Метод Гауса з послідовним виключенням невідомих (базовий метод)засновано [4] на алгоритмі, в основі якого лежить послідовне виключення невідомих вектора 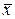з усіх рівнянь, починаючи з (і+1)–го, шляхом елементарних перетворень: перемноження обох частин рівняння на будь-яке число, крім нуля; додавання (віднімання) до обох частин одного рівняння відповідних частин другого рівняння, помножених на будь-яке число, крім нуля.

Суть алгоритмурозглянемо на прикладі системи, яка складається з трьох лінійних алгебраїчних рівнянь з трьома невідомими:

 

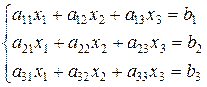(2.3)

 

1) Перевіримо, щоб принаймні один із коефіцієнтів , , 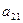не дорівнював нулю. Якщо, наприклад, , тоді необхідно переставити рівняння так, щоб коефіцієнт при x₁ у першому рівнянні не дорівнював нулю.

2) Обчислюється множник:

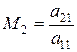. (2.4)

3) Перше рівняння системи (2.3) множиться на і віднімається від другого рівняння системи, отриманої після перестановки рівнянь, якщо вона була необхідною. Результат обчислення має вигляд:

, (2.5)

але 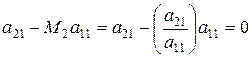. (2.6)

Тоді виключається із другого рівняння.

Позначимо нові коефіцієнти:

 

(2.7)

 

Тоді друге рівняння системи (2.3) набуває вигляду:

 

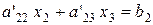. (2.8)

 

Далі необхідно звільнитися від коефіцієнта при в третьому рівнянні системи (2.3) за аналогічним алгоритмом

4) Обчислюється множник для третього рівняння:

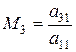. (2.9)

5) Перше рівняння системи (2.3) множиться на 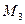і віднімається від третього рівняння. Коефіцієнт при стає нулем, і третє рівняння набуває вигляду:

 

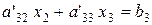, (2.10)

де , (2.11)

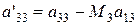, (2.12)

. (2.13)

 

Перетворена таким чином система рівнянь (2.3) набуває вигляду:

 

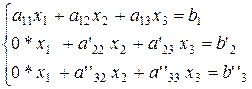(2.14)

 

Ця система рівнянь еквівалентна початковій і має певні переваги, оскільки входить тільки до першого рівняння. Спробуємо тепер виключити 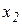з останнього рівняння. Якщо , а 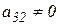, тоді переставимо друге й третє рівняння так, щоб . Інакше система вироджена і має безліч розв’язків.

7) Обчислюємо множник . (2.15)

8) Друге рівняння системи (2.11) помножується на М₃¢¢ і віднімається від 3‑го рівняння:

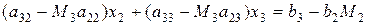. (2.16)

При цьому коефіцієнт біля дорівнює нулю:

 

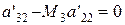, (2.17)

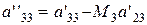, (2.18)

, (2.19)

Отримаємо . (2.20)

Замінивши в системі (2.14) третє рівняння на (2.20), отримаємо систему рівнянь виду:

(2.21)

Таку систему називають системою з трикутною матрицею коефіцієнтів, що еквівалентна СЛАР (2.3). Процес знаходження такої системи називається прямим ходом Гауса. Знайти розв’язок такої системи просто: із 3-го рівняння знайти 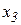, підставити результат у друге і знайти 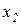, підставити 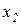і 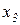в 1-е рівняння системи (2.21) і знайти за формулами:

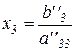, (2.22)

, (2.23)

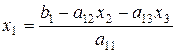. (2.24)

Процес знаходження вектора розв’язку системи (2.3) називають зворотнім ходом метода Гауса [4, 13, 24, 28].

На рисунку 2.2 показана схема алгоритму метода Гауса з послідовним виключенням для розв’язання системи із N рівнянь з N невідомими. Ця схема відповідає розглянутому алгоритму і може бути використана при розробці програми. Блок “Перестановка рівнянь так, щоб 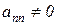” означає деякий алгоритм, який дає змогу не допустити помилки “ділення на 0”. Якщо прямувати до можливого зменшення помилок округлення, то можна використати алгоритм з вибиранням головного елементу.

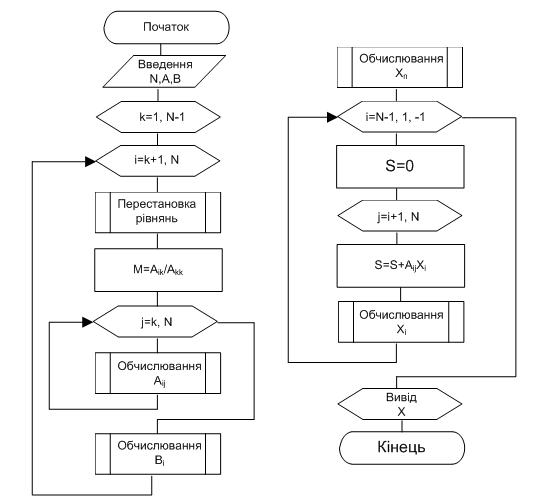
Рисунок 2.2. – Схема алгоритму розв’язання системи лінійних алгебраїчних рівнянь методом Гауса.

 

Призначення індексів в схемі алгоритму (рисунку 2.2):

к– номер рівняння, яке віднімається від інших, а також номер невідомого, яке виключається із залишених к-рівнянь;

i– номер рівняння, із якого в даний момент виключається невідоме;

j– номер стовпця.