рефераты конспекты курсовые дипломные лекции шпоры

Раздел Математика
/
Метод Гауса-Жордана

Реферат Курсовая Конспект

Выберите учебное заведение

Метод Гауса-Жордана

Метод Гауса-Жордана - раздел Математика, Лекція № 2 ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ НА ЕОМ Особливістю Метода Гауса-Жордана [1, 4, 12] Є Перетворення Системи (2.1) (Пря...

Особливістю метода Гауса-Жордана [1, 4, 12] є перетворення системи (2.1) (прямий хід) до еквівалентної з одиничною матрицею коефіцієнтів виду:

, (2.41)

тобто системи, яка містить тільки одиничну діагональ.

Для отримання такої системи в прямий хід алгоритму базового методу Гауса (з послідовним виключенням невідомих) додатково вводяться такі дії:

1. Організація циклу по k по всім рівнянням від 1 до N-1 (k = 1, 2, …, N-1).

2. Процедура вибору головного елементу в кожному k-му стовпці при ;

3. Процедура нормування k-го рівняння системи, тобто в k–му рівнянні кожен коефіцієнт a_k_jрозділити на , включаючи 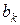, так, щоб коефіцієнт =1.

4. Перетворення всіх рівнянь системи, починаючи з 1–го до N у відповідності з базовим алгоритмом Гауса з метою отримати еквівалентну систему з одиничною діагоналлю. В даному випадку для розрахунку коефіцієнтів a_i_jвикористовуються ті самі формули, що і в базовому алгоритмі Гауса:

; ; ,

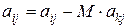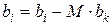але використовуються вони для всіх рівнянь з 1–го до N крім k–го, в якому остається коефіцієнт рівний одиниці.

5. Кінець циклу по k.

Обернений хід методу Гауса-Жордана дуже простий і використовує наступні формули:

x_{k=b k}, при k=1,2,…,n.

Схема алгоритму методу Гауса-Жордана представлена на рисунку 2.6.

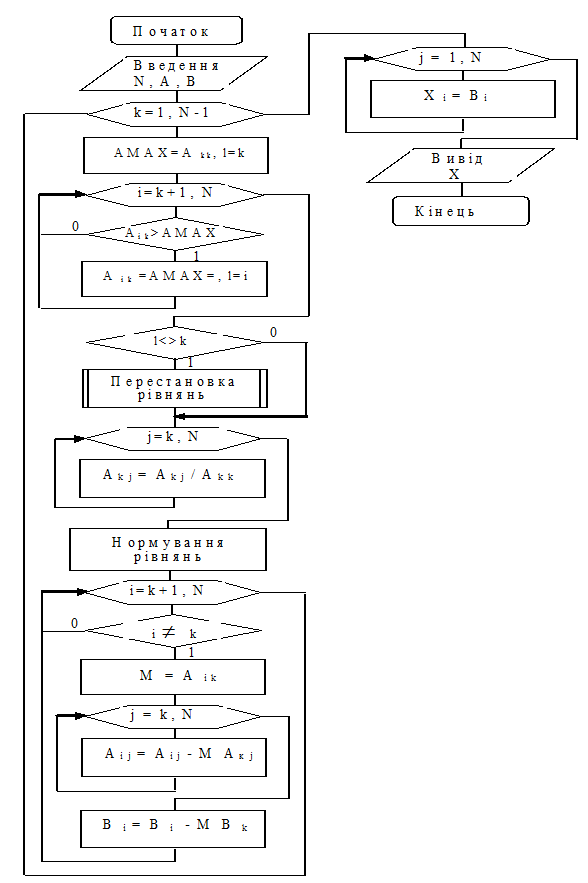
Рисунок 2.6. – Схема алгоритму методу Гауса-Жордана

Развернуть

Открыть в широком формате

– Конец работы –

Эта тема принадлежит разделу:

Лекція № 2 ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ НА ЕОМ

На сайте allrefs.net читайте: Лекція № 2.

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Метод Гауса-Жордана

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

ЧИСЕЛЬНІ МЕТОДИ РОЗВ’ЯЗАННЯ СИСТЕМ ЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ НА ЕОМ
Інженеру часто доводиться вирішувати алгебраїчні і трансцендентні рівняння і системи рівнянь, що можуть являти собою самостійну задачу (наприклад, аналіз рівноваги сил в жорсткій системі балок, або

Основні поняття та визначення
Системою лінійних алгебраїчних рівнянь (СЛАР) [4, 5,12] називають систему виду: (2.1)

Класифікація методів розв’язання СЛАР на ЕОМ
Для розв’язання СЛАР на ЕОМ традиційно використовують [1-5, 8, 10, 11, 13, 24-28, 36, 37, 39] дві групи чисельних методів, що представлені на рисунку 2.1: ü точні (ме

Особливості методів Гауса
Найбільш відомим з точних методів розв’язання системи лінійних алгебраїчних рівнянь (2.1) є методи Гауса, суть яких полягає в тому, що система рівнянь, яка розв’язується, зводиться до еквівалентної

Метод Гауса з послідовним виключенням невідомих
Метод Гауса з послідовним виключенням невідомих (базовий метод)засновано [4] на алгоритмі, в основі якого лежить послідовне виключення невідомих вектора

Метод Гауса за схемою Халецького
Алгоритм метода включає також прямий і зворотній хід. Кінцевою метою прямого ходу є отримання СЛАР, яка еквівалентна заданій, з верхньою трикутною матрицею коефіцієнтів. Для цього матрицю коефіцієн

Метод Гауса з вибором головного елемента
Ідея цього методу виникла [4, 13, 24, 28] у зв’язку з тим, що коефіцієнти СЛАР є параметрами реальних інженерних систем та в більшості є наближеними значеннями, тому що отримані звичайно в результа

Метод Гауса з одиничними коефіцієнтами
В цьому методі зроблена спроба [1, 4, 12, 24, 28] зменшити недоліки перших двох методів пов’язаних з багаторазовим діленням одного наближеного числа на інше. Для цього перед введенням масштабного м

Питання та задачі до самостійної роботи
1. Яку систему називають системою лінійних алгебраїчних рівнянь? 2. Що називається розв'язком СЛАР? 3. Яка система називається сумісною і несумісною? 4. Яка система назив