Метод Гауса з одиничними коефіцієнтами

В цьому методі зроблена спроба [1, 4, 12, 24, 28] зменшити недоліки перших двох методів пов’язаних з багаторазовим діленням одного наближеного числа на інше. Для цього перед введенням масштабного множника k - те рівняння системи ділиться один раз на діагональний елемент 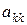так, щоб коефіцієнт при 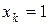, а масштабний множник М_і буде дорівнювати a_{k j.} Результатом прямого ходу є система, еквівалентна СЛАР (2.1), з одиничними коефіцієнтами на головній діагоналі виду:

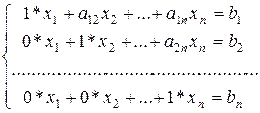(2.39)

Дана система схожа на систему (2.2), яка отримується в результаті прямого ходу базового методу Гауса з послідовним вилученням невідомих і відрізняється від неї тільки діагональними коефіцієнтами. Для отримання такої системи необхідно використовувати алгоритм, який включає в себе наступні етапи:

1. Організація циклу по всім рівнянням від 1 до N-1 (k = 1, 2, …, N-1).

2. В кожному k-му стовпці визначається номер l-го рівняння з головним елементом (тобто номер l -го рівняння, в якому знаходиться коефіцієнт при 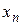зі всіх рівнянь починаючи з k-го до N-го).

3. Якщо номер цього рівняння l не дорівнює k (l<>k), тоді необхідно переставити місцями l-е рівняння з k-м.

4. Нормування k-го рівняння, тобто ділення всіх коефіцієнтів k-го рівняння на 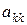(головний елемент при 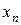), включаючи .

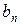5. Перетворення всіх і-х рівнянь, починаючи з (k+1) до N у відповідності з базовим алгоритмом Гауса з метою отримати еквівалентну систему з верхньою трикутною матрицею коефіцієнтів.

6. Кінець циклу по k.

Формула зворотного ходу для систем виду (2.39) спрощується і має вигляд:

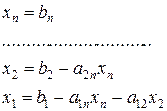(2.40)

Схема алгоритму методу Гауса з одиничними діагональними коефіцієнтами наведена на рисунку 2.5.

Рисунок 2.5. – Схема алгоритму метода Гауса з одиничними коефіцієнтами