Метод конечных элементов

В настоящее время метод конечных элементов (МКЭ) является одним из наиболее популярных методов решения краевых задач в САПР. В математическом отношении метод относится к группе вариационно-разностных. Строгое доказательство таких важных свойств, как устойчивость, сходимость и точность метода, проводится в соответствующих разделах математики и часто представляет собой непростую проблему.

К основным преимуществам МКЭ относят доступность и простоту его понимания и применимость метода для задач с произвольной формой области решения, возможность создания на основе метода высококачественных универсальных программ для ЭВМ.

В МКЭ исходная область определения функции разбивается с помощью сетки, в общем случае неравномерной, на отдельные подобласти - конечные элементы. Искомая непрерывная функция аппроксимируется кусочно-непрерывной, определенной на множестве конечных элементов. Аппроксимация может задаваться произвольным образом, чаще всего для этих целей используются полиномы, которые подбираются так, чтобы обеспечить непрерывность искомой функции в узлах на границах элементов.

Для двухмерных областей наиболее часто используются элементы в форме треугольников и четырехугольников. При этом элементы могут иметь как прямо-, так и криволинейные границы, что позволяет с достаточной степенью точности аппроксимировать границу любой формы.

Для трехмерных областей наиболее употребимы элементы в форме тетраэдра и параллелепипеда, которые также могут иметь прямолинейные и криволинейные границы.

 

Пример использования МКЭ для расчета одномерного температурного поля в однородном стержне. Пусть имеется стержень длиной L и площадью поперечного сечения S (рис. 1).

Один конец стержня жестко закреплен, и к нему подводится тепловой поток q заданной интенсивности. На свободном конце стержня происходит конвективный теплообмен с внешней средой. Известны коэффициент теплообмена 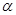и температура окружающей среды Т_*. Вдоль боковой поверхности стержень теплоизолирован.

 

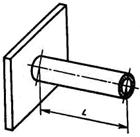
Рис. 1. Однородный стержень, находящийся под воздействием теплового потока

 

Температурное поле в стержне описывается уравнением теплопроводности, которое в одномерном приближении имеет вид

(1)

Краевые условия определяются уравнениями:

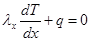при х = 0; (2 а)

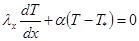при x=L. (2 б)

Искомое температурное поле является непрерывной функцией координаты х (рис. 2, а).

 

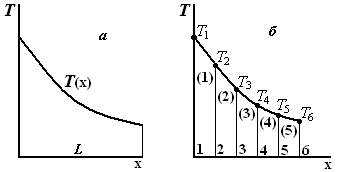
Рис. 2. Расчет одномерного температурного поля в однородном стержне методом МКЭ.

 

В МКЭ стержень разбивается произвольным образом на конечные элементы, которые в данном случае являются отрезками неравной длины. На каждом элементе непрерывная функция Т(х) аппроксимируется некоторой линейной зависимостью, как показано на рис. 2, б (в скобках указаны номера элементов). Аппроксимирующая кусочно-линейная функция определяется через узловые значения T₁-Т₆, которые в общем случае сначала неизвестны и подлежат определению в МКЭ.

 

В общем случае алгоритм МКЭ состоит из четырех этапов:

Этап 1. Выделение конечных элементов (разбиение заданной области на конечные элементы).

Этап 2. Определение аппроксимирующей функции для каждого элемента (определение функции элемента). На данном этапе значение непрерывной функции 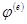в произвольной точке е-го конечного элемента аппроксимируется полиномом 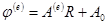, где А^(е) - вектор-строка коэффициентов полинома; А_о - свободный член; R=(х, у, z) - вектор координат в рассматриваемой точке.

Задача этапа заключается в определении неизвестного вектора А^(е) и свободного члена А_о. Для этого, используя условие непрерывности функции в узлах, коэффициенты полинома выражают через вектор Ф^(е) узловых значений функции и координаты узлов и, проделав эквивалентные преобразования, получают

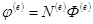(3)

где N^(е) - матрица-строка, элементы которой называют функциями формы конечного элемента.

Функции формы легко вычисляются в каждой точке конечного элемента через координаты самой точки и координаты узлов элемента.

Этап 3. Объединение конечных элементов в ансамбль. На этом этапе уравнения (4), относящиеся к отдельным элементам, объединяются в ансамбль, т. е. в систему алгебраических уравнений:

(4)

Система (5) является моделью искомой непрерывной функции.

Этап 4. Определение вектора узловых значений функции. В общем случае вектор Ф в (5) вначале неизвестен. Его определение - наиболее сложная процедура в МКЭ.

Разработано несколько алгоритмов вычисления вектора Ф. Один из алгоритмов основан на минимизации функционала, связанного с физическим смыслом решаемой задачи, он состоит из 4-х этапов.

Найденные значения вектора Ф подставляют в (4), после чего значение функции 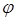легко вычисляется в любой точке заданной области.

 

Рассмотрим подробно этапы алгоритма МКЭ.

Этап 1: выделение конечных элементов.

Разбиение области на элементы - важный этап в МКЭ. От качества разбиения во многом зависит точность получаемых результатов. Например, разбиение на двухмерные элементы, близкие по форме к равносторонним треугольникам, обеспечивает лучшие результаты по сравнению с разбиением на вытянутые по форме треугольные элементы. Возможность легко варьировать размерами элементов - важное свойство МКЭ.

Разбиение области на элементы обычно начинают от ее границы с целью наиболее точной аппроксимации формы границы, затем производится разбиение внутренних областей. Часто разбиение области на элементы производят в несколько этапов. Сначала область разбивают на достаточно крупные подобласти (подконструкции), границы между которыми проходят там, где изменяются свойства материала, геометрия, приложенная нагрузка и пр. Затем каждая подобласть взбивается на элементы. Резкого изменения размеров конечных элементов на границах подобластей стараются избегать. На рис. 3. приведен пример разбиения двухмерной области произвольной формы на треугольные конечные элементы с криволинейными границами.

 

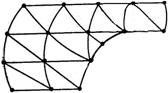
Рис. 3. Разбиение двухмерной области произвольной формы на треугольные конечные элементы с криволинейными границами.

 

Нумерация узлов элементов (глобальная нумерация узлов) - следующая процедура этапа выделения конечных элементов. Порядок нумерации имеет в данном случае существенное значение, так как влияет на эффективность последующих вычислений.

Матрица коэффициентов системы линейных алгебраических уравнений, к которой приводит МКЭ, - сильно разреженная матрица ленточной структуры. Ненулевые элементы такой матрицы располагаются параллельно главной диагонали (рис. 4).

 

Рис. 4. Матрица ленточной структуры.

 

Целое число L, представляющее собой наибольшую разность между номерами ненулевых элементов в строке, называется шириной полосы. Чем меньше ширина полосы, тем меньший объем ОП требуется для хранения матрицы при реализации МКЭ в САПР и тем меньше затраты машинного времени на решение результирующей системы уравнений. Ширина полосы зависит, в свою очередь, от числа степеней свободы узлов и способа нумерации последних.

Под числом степеней свободы понимают количество неизвестных функций, определяемых в каждом узле. Так, например, для двухмерных задач гидравлики в каждом узле определяют три переменные: давление и составляющие скорости по осям X и Y.

При нумерации узлов предпочтителен способ, обеспечивающий минимальную разность между номерами узлов в каждом отдельном элементе. Если максимальную разность между номерами узлов для отдельного элемента обозначить N, а число степеней свободы - М, то ширина полосы

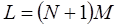
В некоторых случаях уменьшение числа N может быть достигнуто последовательной нумерацией узлов при движении в направлении наименьшего размера рассматриваемой области.

На рис. 5 приведены два различных способа нумерации узлов произвольной области, разбитой на конечные элементы. При первом способе (рис. 5, а) N = 14, при втором (рис. 5, б) N = 5. Ширина полосы для представленных способов при одной степени свободы в узле получается равной соответственно 15 и 6; при двух степенях свободы - 30 и 12. Рациональная нумерация в случае рис. 5, б сокращает необходимый объем ОП почти в три раза по сравнению со случаем рис. 5, б.

 

Рис. 5. Способы нумерации узлов при разбиении двухмерной области на конечные элементы.

 

Информация о способе разбиения области на конечные элементы и нумерации узлов является исходной для всех следующих этапов алгоритмов МКЭ при реализации метода в САПР. При этом требуется указывать не только номер, но и координаты каждого узла и его принадлежность к определенным конечным элементам. Такого рода информация называется топологической и обычно содержит примерно в 6 раз больше чисел, чем количество узлов системы.

При описании области, разбитой на конечные элементы, необходимо задавать: тип конечного элемента; его порядковый номер; номера узлов элемента; координаты узлов, информацию о соединении элементов между собой; значение физических параметров объекта в пределах каждого конечного элемента. Промышленная эксплуатация программной системы долгое время тормозилась именно сложностью подготовки исходных данных, объем которых в некоторых случаях достигал нескольких сотен тысяч.

Усилия разработчиков программ МКЭ в составе САПР в последние годы были направлены на создание подсистем автоматизированной подготовки топологической информации, основу которых составляют специальные программы, называемые препроцессорами. Препроцессоры либо непосредственно включаются в состав программных комплексов, реализующих МК; либо существуют в виде автономных программ.

Этап 2: определение аппроксимирующей функции элементов.

Эту процедуру можно выполнить один раз для типичного элемента области безотносительно к его топологическому положению в ней. Полученная функция используется далее для всех остальных элементов области того же вида. Эта особенность является важным аспектом МКЭ. Благодаря ей элементы с однажды определенными функциями легко включаются в библиотеку элементов соответствующего программного комплекса. Далее эти элементы применяются для решения разнообразных краевых задач.

В качестве аппроксимирующих функций элементов чаще всего используются полиномы. В зависимости от степени полимома конечные элементы делятся на симплекс-, комплекс- и мультиплекс-элементы. Полиномы симплекс-элементов содержат константы и линейные члены; полиномы комплекс-элементов - константы, линейные члены, а также члены более высоких степеней. Комплекс-элементы, как правило, кроме граничных имеют дополнительные внутренние узлы. Полиномы мультиплекс-элементов также содержат члены более высоких степеней. На мультиплекс-элементы накладывается дополнительное условие: их границы должны быть параллельны координатным осям.

Одномерный симплекс-элемент представляет собой отрезок (рис. 6).

 

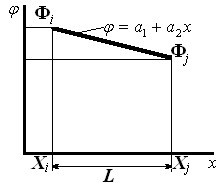
Рис. 6. Одномерный симплекс-элемент.

 

При определении функции этого элемента для простоты будем считать, что узловые значения искомой непрерывной функции, определенные на концах отрезка, известны. По длине отрезка значение функции 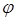аппроксимируется полиномом:

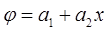(5)

Коэффициенты 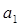и определяются через узловые значения функции и в соответствии с условием непрерывности:

(6)

Подставив (6) в (5), получим систему уравнений:

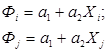
решая, которую определим 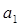и :

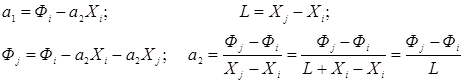
т.е.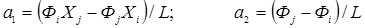

Подставив вычисленные значения коэффициентов аппроксимирующего полинома в (5), получим

Проведем эквивалентные преобразования правой части:

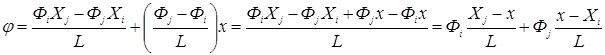(7)

 

Члены полученного уравнения, заключенные в скобки, являются функциями формы одномерного симплекс-элемента:

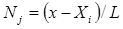; (8)

С учетом обозначений (8) уравнение (7) принимает вид

(9)

или в матричной форме

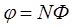(10),

где - матрица-строка; - вектор-столбец.

Функция формы обладает следующим свойством: функция формы с номером i равна 1 в узле с соответствующим номером и равна 0 во всех других узлах. Не представляет труда убедиться в наличии этого свойства у функций формы (8).

Этап 3: объединение конечных элементов в ансамбль.

Основу этого этапа составляет замена произвольно назначенных выше номеров узлов i, j, k на номера, присвоенные узлам в процессе разбиения рассматриваемой области. Эта процедура приводит к системе линейных алгебраических уравнений, позволяющей при известных узловых значениях искомой функции получить значение последней в любой точке области.

Рассмотрим процедуру составления ансамбля конечных элементов для сформулированной выше задачи нахождения поля температур в стержне (рис. 2, а). Кусочно-элементная модель области приведена на рис. 2, б, а функция отдельного элемента определяется уравнением (10).

Можно написать следующее соответствие между произвольными номерами i, j, фигурирующими в уравнении (10), и глобальными номерами узлов рассматриваемой дискретной модели для

элемента 1: 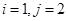(11 а)

элемента 2: (11 б)

элемента 3: (11 в)

элемента 4: 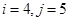(11 г)

элемента 5: (11 д)

Подставив значения номеров узлов (11) в (9), получим:

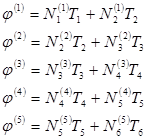(12)

где верхние индексы в скобках относятся к номеру элемента.

В выражениях для функций формы элемента (9) значения произвольных номеров i, j также следует изменить в соответствии с (11). Тогда значения 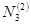, , 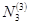например, определяются по формулам:

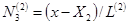
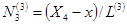
Очевидно, что 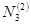и 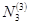не равны друг другу даже в случае равенства длин элементов L⁽²⁾ и L⁽³⁾. При известных значениях узловых величин Т₁-Т₆ уравнения (12) позволяют определить значение температуры в любой точке стержня.

Расширенная форма описания моделей имеет некоторые преимущества при реализации следующих этапов алгоритма МКЭ.