рефераты конспекты курсовые дипломные лекции шпоры

Раздел Философия
/
Логарифмическая амплитудная характеристика и ее построение

Реферат Курсовая Конспект

Выберите учебное заведение

Логарифмическая амплитудная характеристика и ее построение

Логарифмическая амплитудная характеристика и ее построение - раздел Философия, Раздел 1. Общие сведения о САУ Метод Построения Лчх Состоит В Том, Что Ачх И Фчх Исследуемой...

Метод построения ЛЧХ состоит в том, что АЧХ и ФЧХ исследуемой динамической системы изображают графически в виде непрерывных кривых, причем эти кривые строят в логарифмическом масштабе.

И называются они логарифмическая амплитудная частотная характеристика (ЛАХ) и логарифмическая фазовая частотная характеристика (ЛФЧХ)

При этом ЛАХ строят приближенно в виде наскольких прямолинейных отрезков, называемых асимптотами ЛАХ, что существенно упрощает построение характеристики.

Такие ЛАХ называются асимптотическими

Как известно, между АЧХ и ФЧХ существует однозначная связь, следовательно можно ограничиться только построением ЛАХ, так как в ней содержится вся информация о САУ.

Если в САУ такая связь существует, такая система называется минимально-фазаовой, мы рассматриваем именно такие звенья.

То есть: корни характеристических уравнений, соответствующих числителю и знаменателю, имеют отрицательные вещественные части.

Пусть имеется некая ЧПФ

ЛАХ определен как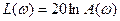

Частота откладывается по оси абсцисс в логарифмическом масштабе, а по оси ординат – значение функции.

Построение асимптотической ЛАХ рассмотрим на примерах.

Пусть

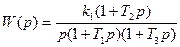
Принято, что постоянные времени нумеруются по убыванию их честленных значений, то есть

Развернуть

Открыть в широком формате

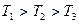
– Конец работы –

Эта тема принадлежит разделу:

Раздел 1. Общие сведения о САУ

Разделы... Основные сведения о САУ Математические методы теории автоматического управления Анализ показателей качества работы САУ...

Если Вам нужно дополнительный материал на эту тему, или Вы не нашли то, что искали, рекомендуем воспользоваться поиском по нашей базе работ: Логарифмическая амплитудная характеристика и ее построение

Что будем делать с полученным материалом:

Если этот материал оказался полезным ля Вас, Вы можете сохранить его на свою страничку в социальных сетях:

Все темы данного раздела:

Назначение и принцип действия замкнутой автоматической системы
Допустим, имеется устройство, состояние которого может быть описано функцией . Назовем ее упра

Составные части замкнутых автоматических систем и их характеристики
Элементом автоматики называется конструктивно законченный элемент, используемый для формирования (построения) автоматической системы – простейший пример – усилитель ЭА хара

Звено с насыщением
2.3. звено с зоной нечувствительности и насыщением

Дифференциальное уравнение линейной САУ и ее передаточная функция
Основной характеристикой любой динамической системы, наиболее полно отражающей ее свойства, является дифференциальное уравнение. Процессы, описывающие линейную САУ, соответ

Последовательное соединение звеньев.
Пример – предыдущая схема Соединение, при котором выходная величина звена является входной

ПФ для ошибки по помехе
Всякая реальная АС работает в условиях помех (шумы усилителя, помехи дискриминатора). Помеха может быть приложена к любой точке системы (в отличие от задающего воздействия, которое прикладывается т

Временные характеристики САУ
Временная характеристика – это отклик САУ на некоторое типовое входное воздействие. При известной ПФ системы

Частотные характеристики САУ
Частотные методы исследования АС основаны на рассмотрении установившейся реакции системы на гармоническое входное воздействие Используется в задачах анализа АС (Дл

Порядок определения АЧХ, ФЧХ и АФК
Передаточная функция системы, как известно, определяется как Частотная пере

Алгоритм нахождения характеристик
Пусть известны ПФ и замкнутой, или

Изодромное звено
Результат параллельного соединения интегрирующего и безынерционного звеньев

Многомерные системы регулирования
К многомерным относятся системы управления и регулирования, имеющие несколько регулируемых величин М